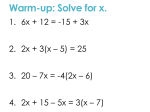Download Linear Inequalities in Two Variables When solving a one

Linear Inequalities in Two Variables
When solving a one variable linear inequality, rather than a
single numerical solution, we found a range of solutions and
were able to indicate that range of solutions on a number line.
Similarly, the solution to a two variable inequality will result in
a solution area.
Graphing a two variable linear inequality has three steps:
1. Find two points: Replace the inequality sign with an equality
sign. Find two points for the line as we have when graphing a
linear equation.
2. Determine the type of line: For > and <, use a dashed line to
indicate that the line is a border but not included in the solution.
For > and <, use a solid line to indicate that the line is a border and
is included in the solution.
3. Determine the solution area: Pick a test point on one side of the
line or the other (it doesn’t matter which side). Make sure the test
point is not on the line. Substitute the test point into the inequality.
If the resulting statement is true, the test point is a solution and
must lie in the solution area - shade the side containing the test
point. If the resulting statement is false, the test point is not a
solution, and the other side is the solution area - shade the other
side.
Example 1: Graph: y > 2x – 3
1. Find two points: y = 2x – 3
x
1
0
y
y = 2(1) – 3
y=2–3
y = -1
Complete the table of values
y = 2(0) – 3
y=0–3
y = -3
x
1
0
y
-1
-3
2. The inequality is > which indicates a solid line
y
6
4
2
6
4
2
2
4
6
x
2
4
6
3. Test point: Since 0’s are easy to work with, we’ll pick (0, 0).
0 > 2(0) – 3
0>0–3
0 > -3
True, so (0, 0) is a solution
y
6
4
Solution
2
6
4
2
2
Area 2
4
6
x
4
6
Example 2: Graph: 5x – 2y > 4
1. Find two points: 5x – 2y = 4
x
y
0
Complete the table of values
0
5x – 2(0) = 4
5x – 0 = 4
5x
=4
5(0) – 2y = 4
0 – 2y = 4
- 2y = 4
x=
y = -2
x
y
0
0
-2
Since the first ordered pair contains a fraction, we might a third:
Let y=3 so 5x – 2(3) = 4
5x – 6 = 4
+6+6
5x = 10
x=2
the order pair: (2, 3)
2. The inequality is > which indicates a dashed line
y
6
4
2
4
6
2
2
4
6
x
2
4
6
3. Test point: Since 0’s are easy to work with, we’ll pick (0, 0).
5(0) – 2(0) > 4
0–0>4
0>4
False, so (0, 0) is not a solution
Shade the other side
y
6
4
2
6
4
2
Solution
2
2
4
Area
6
x
4
6
Example 3: Graph: y < -2
1. Find two points: y = -2
This is a horizontal line with all y’s = -2
x
y
-2
-2
Complete the table of values
Since all of the y-values are -2, we can pick any numbers for x.
x
-3
4
y
-2
-2
To get a good range, let’s
pick a negative number and
a positive number.
2. The inequality is < which indicates a solid line
y
6
4
2
6
4
2
2
4
6
x
2
4
6
3. Test point: Again, we can use (0, 0)
0 < -2
True, so (0, 0) is a solution
y
6
4
2
6
4
2
2
4
2
Solution4
6
Area
6
x