Exponential and Logarithmic Functions
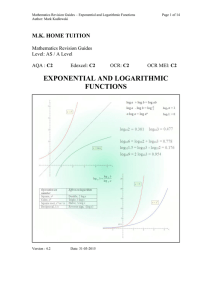
... EXPONENTIAL AND LOGARITHMIC FUNCTIONS An exponential function is one whose variable is a power or exponent. Any function of the form f (x) = ax , where a is a non-zero positive constant, is an exponential function. The graphs on the right are of two such exponential functions: y = 2x and y = 5x. All ...
... EXPONENTIAL AND LOGARITHMIC FUNCTIONS An exponential function is one whose variable is a power or exponent. Any function of the form f (x) = ax , where a is a non-zero positive constant, is an exponential function. The graphs on the right are of two such exponential functions: y = 2x and y = 5x. All ...
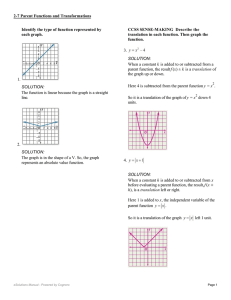
Identify the type of function represented by each graph. 1
... eSolutions Manual - Powered by Cognero h), is a translation left or right. When a constant k is added to or subtracted from a parent function, the result f (x) ± k is a translation of ...
... eSolutions Manual - Powered by Cognero h), is a translation left or right. When a constant k is added to or subtracted from a parent function, the result f (x) ± k is a translation of ...
9.1 The Square Root Function
... Let’s create a table of points that satisfy the equation of the function, then plot the points from the table on a Cartesian coordinate system on graph paper. We’ll continue creating and plotting points until we are convinced of the eventual shape of the graph. We know we cannot take the square root ...
... Let’s create a table of points that satisfy the equation of the function, then plot the points from the table on a Cartesian coordinate system on graph paper. We’ll continue creating and plotting points until we are convinced of the eventual shape of the graph. We know we cannot take the square root ...
Centrality

In graph theory and network analysis, indicators of centrality identify the most important vertices within a graph. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, and super-spreaders of disease. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.They should not be confused with node influence metrics, which seek to quantify the influence of every node in the network.