* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Congruence graphs and newforms
Survey
Document related concepts
Transcript
Congruence graphs and newforms
Congruence graphs and newforms
Samuele Anni (IWR - Universität Heidelberg)
Vandita Patel (University of Warwick)
work in progress
joint with
Number Theory and Geometry Seminar,
University of Nottingham, 9th December 2016
Congruence graphs and newforms
The theory of congruences between modular forms is a central topic in
contemporary number theory.
Congruences are a display of the interplay between geometry and
arithmetic.
Congruence graphs and newforms
Congruences
1
Congruences
2
Congruence graphs
3
Checking congruences
4
Conjectures and congruence graphs
5
Data collected
Congruence graphs and newforms
Congruences
Modular forms
Let n be a positive integer, the congruence subgroup Γ0 (n) is a subgroup
of SL2 (Z ) given by
a b
Γ0 (n) =
∈ SL2 (Z ) : n | c .
c d
Given a pair of integers n (level) and k (weight), a modular form f for
Γ0 (n) is an holomorphic function on the complex upper half-plane H
satisfying
az + b
f (γz) = f
= (cz + d)k f (z) ∀γ ∈ Γ0 (n), z ∈ H
cz + d
and a growth condition for the coefficients of its power series expansion
f (z) =
∞
X
0
an q n ,
where
q = e 2πiz .
Congruence graphs and newforms
Congruences
Newforms
There are families of operators acting on the space of modular forms. In
particular, the Hecke operators Tp for every prime p. These operators
describe the interplay between different group actions on the complex
upper half-plane.
We will consider only cuspidal newforms: cuspidal modular forms
(a0 = 0), normalized (a1 = 1), which are eigenforms for the Hecke
operators and arise from level n.
We will denote by S(n, k)C the space of cuspforms and by S(n, k)new
the
C
subspace of newforms.
Congruence graphs and newforms
Congruences
Congruence between newforms
Let f and g be two newforms.
X
f =
am q m
g=
X
bm q m .
Then Q ({am }) is a number field, called Hecke eigenvalue field of f .
Definition
We say that f and g are congruent mod p, if there exists an ideal p
above p in the compositum of the Hecke eigenvalue fields of f and g
such that
am ≡ bm mod p for all m.
Congruence graphs and newforms
Congruences
Example: S(77, 2)new
C
f0 (q) = q − 3q 3 − 2q 4 − q 5 − q 7 + 6q 9 − q 11 + 6q 12 − 4q 13 + 3q 15 + . . .
f1 (q) = q + q 3 − 2q 4 + 3q 5 + q 7 − 2q 9 − q 11 − 2q 12 − 4q 13 + 3q 15 + . . .
f2 (q) = q + q 2 + 2q 3 − q 4 − 2q 5 + 2q 6 − q 7 − 3q 8 + q 9 − 2q 10 + q 11 + . . .
f3,4 (q) = q + αq 2 + (−α + 1) q 3 + 3q 4 − 2q 5 + (α − 5) q 6 + q 7 + αq 8 + . . .
where α satisfies x 2 − 5 = 0.
√
The Hecke eigenvalue fields are Q for f0 , f1 , f2 and Q ( 5) for f3 and f4 .
The following congruences hold:
f0 ≡ f1 mod 2,
f1 ≡ f3,4 mod p5 ,
√
where p2 , p5 are primes in Q ( 5).
f2 ≡ f3,4 mod p2 ,
This is the complete list of possible congruences!
Congruence graphs and newforms
Congruence graphs
1
Congruences
2
Congruence graphs
3
Checking congruences
4
Conjectures and congruence graphs
5
Data collected
Congruence graphs and newforms
Congruence graphs
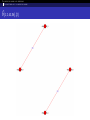
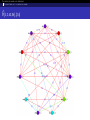
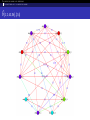
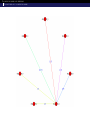
Congruence Graphs
Vertices : each vertex in the graph corresponds to a Galois orbit
of newforms of level and weight in a given set.
Edges : an edge between two vertices is drawn if there exists a
prime p such that a congruence mod p holds between two forms in
the Galois orbits considered.
Let S be the set of divisors of a positive integer and let W be a finite
set of weights, we will denote by GS,W the associated graph.
Congruence graphs and newforms
Congruence graphs
G[1,7,11,77],[2]
Congruence graphs and newforms
Congruence graphs
G[1,2,3,5,6,10,15,30],[2,4]
Congruence graphs and newforms
Congruence graphs
G[1,19],[2,4]
Congruence graphs and newforms
Congruence graphs
G[1,19],[2,4,6]
Congruence graphs and newforms
Congruence graphs
G[1,2,4,8,16,32,64,128],[4]
Congruence graphs and newforms
Checking congruences
1
Congruences
2
Congruence graphs
3
Checking congruences
4
Conjectures and congruence graphs
5
Data collected
Congruence graphs and newforms
Checking congruences
How do we check congruence?
Sturm Theorem
P
Let n ≥ 1 be an integer. Let f (q) = am q m be a modular form of level
n and weight k, with coefficients in a discrete valuation ring R. Suppose
that the reduction of the q-expansion of f has am = 0 for all
m≤
k
[SL2 (Z ) : Γ0 (n)] : = B(n, k).
12
Then am = 0 for all m.
Suppose n ≥ 5. Sturm Theorem then follows from the fact that the line
bundle of modular forms of weight k on X (n)C has degree:
deg(ω ⊗k ) =
k
· [SL2 (Z ) : Γ0 (n)].
24
Considering automorphisms, so we obtain the Sturm bound.
Congruence graphs and newforms
Checking congruences
Theorem (Kohnen+)
Let k1 , k2 ≥ 2 and n be positive integers. Let f1 , f2 be modular forms of
level n and weight k1 , k2 respectively. Let ` be a prime number. Assume
that the q-expansions of f1 and f2 have coefficients in the ring of integers
of a number field, and let λ be a maximal ideal herein such that (`) ⊂ λ.
If am (f1 ) = am (f2 ) mod λ for every m such that
(
[SL2 (Z ) : Γ0 (n) ∩ Γ1 (`)] if ` > 2,
max {k1 , k2 }
·
m≤
12
[SL2 (Z ) : Γ0 (n) ∩ Γ1 (4)] if ` = 2
then am (f1 ) = am (f2 ) mod λ for every m.
n ∈ Z >0
Γ1 (n) =
a
c
b
d
∈ SL2 (Z ) : n | a−1 , n | c
.
Congruence graphs and newforms
Checking congruences
The previous results can be combined and enhanced in order to give
bounds to check congruences between newforms (also for general levels).
Anyway, these kind of result rely on number fields arithmetic: if the
form do not have the same Hecke eigenvalue field, one needs to work in
their compositum, and this is generally computationally expensive.
Resultants
In our approach we compute the resultant of the minimal polynomials of
the coefficients, with prime number index, of the q-expansions up to the
Sturm bound. Taking GCDs of several of these resultants we can write a
finite set of “potential” congruence primes and then check the existence
of congruences or discard it.
Congruence graphs and newforms
Conjectures and congruence graphs
1
Congruences
2
Congruence graphs
3
Checking congruences
4
Conjectures and congruence graphs
GL2 -type abelian varieties
Hecke algebra: connectedness
Rayuela conjecture and chain of congruences
5
Data collected
Congruence graphs and newforms
Conjectures and congruence graphs
Motivations
Study of generalizations of Maeda’s conjecture;
Connectedness of Hecke algebras;
Factorization of characteristic polynomials of Hecke operators
modulo primes;
Building databases of mod ` modular Galois representation;
Study of chain of congruences techniques developed by Dieulefait;
Prove cases of base change in the Langlands program;
Study of GL2 -type abelian varieties in positive characteristic.
Congruence graphs and newforms
Conjectures and congruence graphs
Motivations
Study of generalizations of Maeda’s conjecture;
Connectedness of Hecke algebras;
Factorization of characteristic polynomials of Hecke operators
modulo primes;
Building databases of mod ` modular Galois representation;
Study of chain of congruences techniques developed by Dieulefait;
Prove cases of base change in the Langlands program;
Study of GL2 -type abelian varieties in positive characteristic.
Congruence graphs and newforms
Conjectures and congruence graphs
GL2 -type abelian varieties
G[1,7,11,77],[2] : a surface of GL2 -type and two elliptic curves
Congruence graphs and newforms
Conjectures and congruence graphs
Hecke algebra: connectedness
Definition
The Hecke algebra T(n, k) is the Z -subalgebra of EndC (S(n, k)C )
generated by Hecke operators Tp for every prime p.
Question (Ash, Mazur)
Is Spec T(n, k) connected?
When k = 2, yes! This was proved by Mazur.
Congruence graphs and newforms
Conjectures and congruence graphs
k = 2: Mazur geometric argument
Mazur’s proof is only for prime levels. Let J be the Jacobian of the
modular curve X0 (p). Assume that Spec T is not connected then
J∼
= A × B.
If J ∼
= A × B there are no nontrivial homomorphisms from A to B̂ nor
from B to Â, since J decomposes (up to isogenies) as a product of simple
factors with multiplicity one.
The principal polarization of J induces principal polarizations on A and
on B, but a Jacobian cannot decompose as a nontrivial direct product of
principally polarized abelian varieties =⇒ contradiction =⇒ Spec T is
connected.
Congruence graphs and newforms
Conjectures and congruence graphs
The argument can be extended to non-prime levels using the anemic
Hecke algebra.
It is enough to show that the algebra generated only by the Hecke
operators with index prime to the level is connected. This follows using
muliplicity one of the factors of the decomposition of the Jacobian of the
modular curve.
The congruence graphs are related to the dual graphs of the spectrum of
the Hecke algebra of given level and weight.
Congruence graphs and newforms
Conjectures and congruence graphs
primes up to 293 and weight 2
Congruence graphs and newforms
Conjectures and congruence graphs
Open problem when k > 2.
Quote from a talk of William Stein (December 1999)
“Well, the reason why the question is particularly intriguing is that we
don’t seem to have any hope of a proof that mimics the proof for weight
2. The higher weight motives just don’t (yet...) have the precise
algebro-geometric structure that come from principally polarized abelian
varieties. So one would need an utterly different kind of proof, (if the
connectedness property is true... which, after your calculationsa looks
possible).” Mazur, email, yesterday.
a for
k ≤ 8 and p ≤ 53
Verified for primes up to 373 and weight 4, primes up to 293 and weight
up to 8, primes up to 97 weight up to 12.
Congruence graphs and newforms
Conjectures and congruence graphs
primes up to 293 and weight 4
Congruence graphs and newforms
Conjectures and congruence graphs
primes up to 293 and weight 6
Congruence graphs and newforms
Conjectures and congruence graphs
primes up to 97 and weight 10
Congruence graphs and newforms
Conjectures and congruence graphs
primes up to 97 and weight 12
Warning: here there are also forms of level 1!
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,43],[12]
Congruence graphs and newforms
Conjectures and congruence graphs
Conjecture I
Theorem
Spec T(p, k) is connected for p prime ≤ 373 with k = 4, p prime ≤ 293
with k = 6, 8, p prime ≤ 97 with k = 10, 12.
This implies that G[p],[k] is a connected graphs for p and k as above.
Theorem
G[1,p],[4] is a complete graph for p prime ≤ 373.
Conjecture
G[1,p],[4] is a complete graph for all primes p.
Congruence graphs and newforms
Conjectures and congruence graphs
Conjecture II
The graph GS,W may not be connected. The computations suggest the
following conjecture:
Conjecture
Given S and W , there exists a finite set W 0 , with W ⊆ W 0 , such that
the graph GS,W 0 is connected.
This conjecture is a theorem if we assume Maeda’s conjecture for level 1
modular forms.
This conjecture is essentially equivalent to the connectedness of the
algebra given by the sum of the Hecke algebras in the levels and weights
considered.
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,7,11,77],[2]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,7,11,77],[2,4,6,8,10]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,2,43,86],[2]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,2,43,86],[2,4]
Congruence graphs and newforms
Conjectures and congruence graphs
Another observation obtained through extensive computations is the
existence of forms which are congruent modulo different primes to
each of the newforms in the set considered.
These forms or at least the connectedness of the graphs may lead to new
results in the chain of congruences techniques developed by Dieulefait
and towards the Rayuela conjecture.
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,2,43,86],[2,4]
Congruence graphs and newforms
Conjectures and congruence graphs
Subgraph of G[1,2,43,86],[2,4]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,19],[2,4]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,19],[2,4,6]
Congruence graphs and newforms
Conjectures and congruence graphs
Congruence graphs and newforms
Conjectures and congruence graphs
Conjecture (Rayuela Conjecture)
Let F be a totally real number field, `0 , `∞ prime numbers and
ρi : Gal(F /F ) → GL2 (F`i ),
i = 0, ∞,
two absolutely irreducible odd Galois representations.
Then there exists a family of odd, absolutely
irreducible, 2-dimensional strictly compatible
systems of Galois representations {ρi,λ }ni=1 such
that:
ρ0 ≡ ρ1,λ0 (mod λ0 ), with λ0 | `0 .
ρ∞ ≡ ρn,λ∞ (mod λ∞ ), with λ∞ | `∞ .
for i = 1, . . . , n − 1 there exist λi prime such
that ρi,λi ≡ ρi+1,λi (mod λi ),
all the congruences involved are MLT (all the
congruences involved are of big, odd and
absolutely irreducible representations).
Congruence graphs and newforms
Conjectures and congruence graphs
Conjecture (Rayuela Conjecture: modular setting)
Let F be a totally real number field, `0 , `∞ prime numbers and
ρi : Gal(F /F ) → GL2 (F`i ),
i = 0, ∞,
two absolutely irreducible odd Galois representations attached to Hilbert
modular newforms f0 and f∞ , respectively. Then there exists a family of
odd, absolutely irreducible, 2-dimensional strictly compatible systems of
Galois representations {ρi,λ }ni=1 such that:
ρ0 ≡ ρ1,λ0 (mod λ0 ), with λ0 | `0 .
ρ∞ ≡ ρn,λ∞ (mod λ∞ ), with λ∞ | `∞ .
for i = 1, . . . , n − 1 there exist λi prime such that ρi,λi ≡ ρi+1,λi
(mod λi ),
all the congruences involved are MLT (all the congruences involved
are of big, odd and absolutely irreducible representations).
Congruence graphs and newforms
Conjectures and congruence graphs
A mod 2 phenomena?
Congruences modulo small primes occurr often. Anyway, removing such
primes and increasing the set of weights the resulting graphs are still
connected.
G[1,2,3,4,6,12],[2,4,6]
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,2,3,4,6,12],[2,4,6] no 2, 3
G[1,2,3,4,6,12],[2,4,6,8] no 2, 3
Congruence graphs and newforms
Conjectures and congruence graphs
G[1,2,3,4,6,12],[2,4,6,8,··· ,32] no 2, 3
Congruence graphs and newforms
Data collected
1
Congruences
2
Congruence graphs
3
Checking congruences
4
Conjectures and congruence graphs
5
Data collected
Congruence graphs and newforms
Data collected
All the computations have been done on a server at the University of
Warwick:
server
hecke
year
2012
speed
2600(MHz)
total cores
64
RAM
512(gb)
disks
19 (tb)
Levels of type pq for p and q primes up to 300 (less when the weight is
higher ∼ 150) and weights up to 12.
Congruence graphs and newforms
Data collected
Data analysis
level up to 360, weights in [2, 4]
level up to 120, weights in
[2, 4, 6, 8, 10]
level up to 360, weights in [2, 4, 6]
level up to 120, weights in
[2, 4, 6, 8, 10, 12]
Congruence graphs and newforms
Data collected
Data analysis: vertices
Congruence graphs and newforms
Data collected
Data analysis: edges
Congruence graphs and newforms
Data collected
Data analysis: number of connected
components
level up to 360, weights in [2, 4]
level up to 360, weights in [2, 4, 6]
Congruence graphs and newforms
Data collected
level up to 120, weights in
[2, 4, 6, 8, 10]
level up to 120, weights in
[2, 4, 6, 8, 10, 12]
Congruence graphs and newforms
Data collected
Questions:
Is it possible to predict the number of edges?
What is the smallest weight for which a given graph becomes
connected?
Extensions to number fields: Hilbert modular forms and Bianchi
forms and extensions to Siegel modular forms.
Relax the requirements: ask for isomorphic mod ` Galois
representations or projective mod ` Galois representations.
Congruence graphs and newforms
Data collected
Congruence graphs and newforms
Samuele Anni (IWR - Universität Heidelberg)
Vandita Patel (University of Warwick)
work in progress
joint with
Number Theory and Geometry Seminar,
University of Nottingham, 9th December 2016
Thanks!