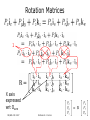
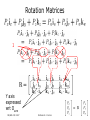
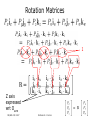
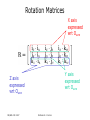
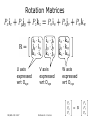
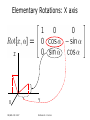
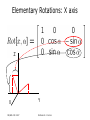
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ferrier_kinematics5
Tensor operator wikipedia , lookup
Oscillator representation wikipedia , lookup
Matrix mechanics wikipedia , lookup
Centripetal force wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Fictitious force wikipedia , lookup
Earth's rotation wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Four-vector wikipedia , lookup
Rotations in 4-dimensional Euclidean space wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
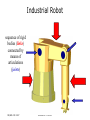
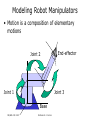
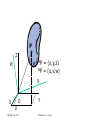
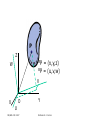
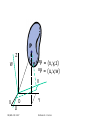
Forward Kinematics Professor Nicola Ferrier ME Room 2246, 265-8793 [email protected] ME/ECE 439 2007 Professor N. J. Ferrier Forward Kinematics • Modeling assumptions • Review: Today – Spatial Coordinates • Pose = Position + Orientation – Rotation Matrices – Homogeneous Coordinates • Frame Assignment – Denavit Hartenberg Parameters • Robot Kinematics – End-effector Position, – Velocity, & – Acceleration ME/ECE 439 2007 Professor N. J. Ferrier Next Lecture Industrial Robot sequence of rigid bodies (links) connected by means of articulations (joints) ME/ECE 439 2007 Professor N. J. Ferrier Robot Basics: Modeling • Kinematics: – Relationship between the joint angles, velocities & accelerations and the end-effector position, velocity, & acceleration ME/ECE 439 2007 Professor N. J. Ferrier Modeling Robot Manipulators • Open kinematic chain (in this course) • One sequence of links connecting the two ends of the chain (Closed kinematic chains form a loop) • Prismatic or revolute joints, each with a single degree of mobility • Prismatic: translational motion between links • Revolute: rotational motion between links • Degrees of mobility (joints) vs. degrees of freedom (task) • Positioning and orienting requires 6 DOF • Redundant: degrees of mobility > degrees of freedom • Workspace • Portion of environment where the end-effector can access ME/ECE 439 2007 Professor N. J. Ferrier Modeling Robot Manipulators • Open kinematic chain – sequence of links with one end constrained to the base, the other to the end-effector End-effector Base ME/ECE 439 2007 Professor N. J. Ferrier Modeling Robot Manipulators • Motion is a composition of elementary motions Joint 2 Joint 1 Joint 3 Base ME/ECE 439 2007 End-effector Professor N. J. Ferrier Kinematic Modeling of Manipulators • Composition of elementary motion of each link • Use linear algebra + systematic approach • Obtain an expression for the pose of the end-effector as a function of joint variables qi (angles/displacements) and link geometry (link lengths and relative orientations) Pe = f(q1,q2,,qn ;l1,ln,1,n) ME/ECE 439 2007 Professor N. J. Ferrier Pose of a Rigid Body • Pose = Position + Orientation • Physical space, E3, has no natural coordinates. • In mathematical terms, a coordinate map is a homeomorphism (1-1, onto differentiable mapping with a differentiable inverse) of a subset of space to an open subset of R3. – A point, P, is assigned a 3-vector: AP = (x,y,z) where A denotes the frame of reference ME/ECE 439 2007 Professor N. J. Ferrier P Z BP AP X A = (x,y,z) = (x,y,z) Y B Y X ME/ECE 439 2007 Z Professor N. J. Ferrier Pose of a Rigid Body • Pose = Position + Orientation How do we do this? ME/ECE 439 2007 Professor N. J. Ferrier Pose of a Rigid Body • Pose = Position + Orientation • Orientation of the rigid body – Attach a orthonormal FRAME to the body – Express the unit vectors of this frame with respect to the reference frame XA YA ZA ME/ECE 439 2007 Professor N. J. Ferrier Pose of a Rigid Body • Pose = Position + Orientation • Orientation of the rigid body – Attach a orthonormal FRAME to the body – Express the unit vectors of this frame with respect to the reference frame XA YA ZA ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices • OXYZ & OUVW have coincident origins at O – OUVW is fixed to the object – OXYZ has unit vectors in the directions of the three axes ix, jy,and kz – OUVW has unit vectors in the directions of the three axes iu, jv,and kw • Point P can be expressed in either frame: ME/ECE 439 2007 Professor N. J. Ferrier P Z AP = (x,y,z) BP = (u,v,w) W V X O Y U ME/ECE 439 2007 Professor N. J. Ferrier P Z AP = (x,y,z) BP = (u,v,w) W V X O Y U ME/ECE 439 2007 Professor N. J. Ferrier P Z AP = (x,y,z) BP = (u,v,w) W V X O Y U ME/ECE 439 2007 Professor N. J. Ferrier P Z AP = (x,y,z) BP = (u,v,w) W V X O Y U ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices 1 X axis expressed wrt Ouvw ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices 1 Y axis expressed wrt Ouvw ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices 1 Z axis expressed wrt Ouvw ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices X axis expressed wrt Ouvw Y axis expressed wrt Ouvw Z axis expressed wrt Ouvw ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices 1 U axis expressed wrt Oxyz ME/ECE 439 2007 Professor N. J. Ferrier Rotation Matrices U axis expressed wrt Oxyz ME/ECE 439 2007 V axis expressed wrt Oxyz Professor N. J. Ferrier W axis expressed wrt Oxyz Properties of Rotation Matrices • Column vectors are the unit vectors of the orthonormal frame – They are mutually orthogonal – They have unit length • The inverse relationship is: – Row vectors are also orthogonal unit vectors ME/ECE 439 2007 Professor N. J. Ferrier Properties of Rotation Matrices • Rotation matrices are orthogonal • The transpose is the inverse: • For right-handed systems – Determinant = -1(Left handed) • Eigenvectors of the matrix form the axis of rotation ME/ECE 439 2007 Professor N. J. Ferrier Elementary Rotations: X axis Z X ME/ECE 439 2007 Y Professor N. J. Ferrier Elementary Rotations: X axis Z X ME/ECE 439 2007 Y Professor N. J. Ferrier Elementary Rotations: Y axis Z X ME/ECE 439 2007 Y Professor N. J. Ferrier Elementary Rotations: Z-axis Z X ME/ECE 439 2007 Y Professor N. J. Ferrier Composition of Rotation Matrices • Express P in 3 coincident rotated frames ME/ECE 439 2007 Professor N. J. Ferrier Composition of Rotation Matrices • Recall for matrices AB BA (matrix multiplication is not commutative) Rot[Z,90] ME/ECE 439 2007 Rot[Y,-90] Professor N. J. Ferrier Composition of Rotation Matrices • Recall for matrices AB BA (matrix multiplication is not commutative) Rot[Z,90] Rot[Y,-90] ME/ECE 439 2007 Professor N. J. Ferrier Rot[Z,90] Rot[Y,-90] ME/ECE 439 2007 Rot[Y,-90] Rot[Z,90] Professor N. J. Ferrier Rot[z,90]Rot[y,-90] Rot[y,-90] Rot[z,90] ME/ECE 439 2007 Professor N. J. Ferrier Decomposition of Rotation Matrices • Rotation Matrices contain 9 elements • Rotation matrices are orthogonal – (6 non-linear constraints) 3 parameters describe rotation • Decomposition is not unique ME/ECE 439 2007 Professor N. J. Ferrier Decomposition of Rotation Matrices • Euler Angles • Roll, Pitch, and Yaw ME/ECE 439 2007 Professor N. J. Ferrier Decomposition of Rotation Matrices • Angle Axis ME/ECE 439 2007 Professor N. J. Ferrier Decomposition of Rotation Matrices • Angle Axis • Elementary Rotations ME/ECE 439 2007 Professor N. J. Ferrier Pose of a Rigid Body • Pose = Position + Orientation Ok. Now we know what to do about orientation…let’s get back to pose ME/ECE 439 2007 Professor N. J. Ferrier Spatial Description of Body • position of the origin with an orientation Z B X A ME/ECE 439 2007 Y Professor N. J. Ferrier Homogeneous Coordinates • Notational convenience ME/ECE 439 2007 Professor N. J. Ferrier Composition of Homogeneous Transformations • Before: • After ME/ECE 439 2007 Professor N. J. Ferrier Homogeneous Coordinates • Inverse Transformation ME/ECE 439 2007 Professor N. J. Ferrier Homogeneous Coordinates • Inverse Transformation Orthogonal: no matrix inversion! ME/ECE 439 2007 Professor N. J. Ferrier