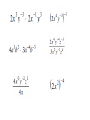Download polynomial operations

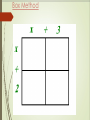
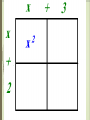
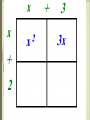
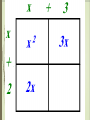
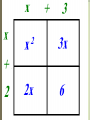
Polynomials
Multiplying Monomials
 Monomial-a number, a variable, or the product of a number
and one or more variables.(Cannot have negative exponent)
› Example:
› -5, ½ , 8
› 3a, a/2 (½ a)
› A2b3
Not Example:
5+a
2a/b
a+b-6
 Constants-monomials that are real numbers
› A number by itself, without a variable (Ex: 4)
When looking at the expression 103,
10 is called the
base
and 3 is called the
exponent or power.
103 means 10 • 10 • 10
103 = 1000
An algebraic expression contains:
1) one or more numbers or variables,
and
2) one or more arithmetic
operations.
Examples:
x-3
4
3 • 2n
1
m
In expressions, there are many
different ways to write
multiplication.
1)
2)
3)
4)
5)
ab
a•b
a(b) or (a)b
(a)(b)
axb
We are not going to use the multiplication symbol any more.
Why?
Division, on the other hand, is
written as:
x
1)
3
2) x ÷ 3
Multiplying Monomials
 To MULTIPLY powers that have the SAME BASE, just
simply ADD the exponents and leave the base the
same.
 Example:
 23 * 25 = 28
 x5 * x = x6 (x is the same as x1and 5 + 1 = 6)
Simplify
1.
3
4
(-7c d )
3
(4cd )
= -28c4d7
2
3
4
2. (5a b c )
3
4
2
(6a b c )
= 30a5b7c6
Find the Power of a Power
 To find the power of a power, multiply the exponents.
 Example:
 (22)3 = 26
Simplify
3
5
1. (p )
=
15
p
2
4
2
2. [(3 ) ]
= 316
Power of a Product
-To find the power of a product, find the power of each factor and multiply.
(a b )m = am bm
EXAMPLE: (-2xy)3 = (-2)3 x3 y3 = -8x3 y3
SIMPLIFY the following:
1). (4ab)2
2). (3y5 z)2
3). [(5cd3)2]3
4). (x + x)2
5). (x3∙x4)3
SIMPLIFYING MONOMIAL EXPRESSIONS
 To simplify an expression involving monomials, write an
expression in which:

1. Each base appears exactly once.

2. There are no powers of powers.

3. All fractions are in simplest form.
 SIMPLIFY (⅓xy4 )2 [(-6y)²]³


your way
→(Remember: Start within your
parentheses and work
out)
Dividing
Monomials
Dividing Powers with the Same Base
 To DIVIDE powers that have the SAME BASE,
SUBTRACT the exponents.
 Quotient of powers: For all integers m and n and any
nonzero number a , am = am-n .

an
 Example: Simplify a⁴ b⁷ = a4-1 b7-2 = a³ b⁵

a b²



Power of a Quotient
 - For any integer m and any real numbers a and b ,

b ≠ 0, ( a / b )m = am / bm .




Simplify
[
2a³b⁵
]3 = (2a³b⁵)³
3b2
( 3b²)³
= 8 a9 b15

27 b6

= 8 a9 b9

27
Power of Zero and Negative Exponents
Zero Exponent : For any nonzero number a , a0 = 1.
 Example: 30 = 1 , x0 = 1
Negative Exponent Property : For any nonzero number a and any integer n, a
n = 1 and 1 = an .
an
a-n
 Example: 4-2 = 1
42
 Example: 1 = 53
5-3
→The simplified form of an expression containing
negative exponents must contain only positive
exponents.
1. 313 / 319
Answer: 3-6 = 1 / 36
2.
(y³z9) / (yz²)
Answer: y2z7
3.
(30h-2 k14 ) / (5hk-3 )
Answer: 6k17
h3
1. b-4
 b-5
2. (-x-1 y)0
4w-1 y2
3. (6a-1 b)2

(b2 )4
4. s-3 t-5
(s2 t3 )-1
5. (2a-2 b)-3

5a2 b4
Stacey has to pick an outfit. She has 6 dresses, 12
necklaces, and 10 pairs of earrings. How many
different outfits can she choose from if she wears 1
dress, 3 necklaces, and a pair of earrings?
Polynomials
Polynomials
 A polynomial is a monomial or a sum of monomials.
 Types of polynomials
 Binomial: sum or difference of two monomials
 Trinomial: sum or difference of three monomials.
Degrees
 Degree of a monomial-the sum of the exponents
 Example: the degree of 8y4 is 4, the degree of 2xy2z3 is
6 (because if you add all the exponents of the
variables you get 6)
Degrees
 Degree of a polynomial-the greatest degree of any term in the
polynomial
 Find the degree of each term, the highest is the degree of the
polynomial
 Example: 4x2y2 + 3x2 + 5
 Find the degree of each term
 4x2y2 has a degree 4
 3x2 has a degree of 2
 5 has no degree
 The greatest is 4, so that’s the degree of the polynomial.
Arrange Polynomials
 Arrange Polynomials in ascending or descending
order
 Ascending-least to greatest
 Descending-greatest to least
 Example: 6x3 –12 + 5x in descending order.
 6x3 + 5x –12
Adding and
Subtracting
Polynomials
 When adding or subtracting polynomials remember to combine
LIKE TERMS.
 Example:
 (3x2 – 4x + 8) + (2x – 7x2 – 5)
 Notice which terms are alike…combine these terms. (They have
been color coded)
 3x2 – 7x2 = -4x2
 – 4x + 2x = -2x
 8–5=3
 So the answer is… -4x2 - 2x + 3
 Be sure to put the powers in descending order.
1. Add the following polynomials:
(9y - 7x + 15a) + (-3y + 8x - 8a)
Group your like terms.
9y - 3y - 7x + 8x + 15a - 8a
6y + x + 7a
2. Add the following polynomials:
(3a2 + 3ab - b2) + (4ab + 6b2)
Combine your like terms.
3a2 + 3ab + 4ab - b2 + 6b2
3a2 + 7ab + 5b2
3. Add the following polynomials
using column form:
(4x2 - 2xy + 3y2) + (-3x2 - xy + 2y2)
Line up your like terms.
4x2 - 2xy + 3y2
+ -3x2 - xy + 2y2
_________________________
x2 - 3xy + 5y2
4. Subtract the following polynomials:
(9y - 7x + 15a) - (-3y + 8x - 8a)
Rewrite subtraction as adding the opposite.
(9y - 7x + 15a) + (+ 3y - 8x + 8a)
Group the like terms.
9y + 3y - 7x - 8x + 15a + 8a
12y - 15x + 23a
5. Subtract the following polynomials:
(7a - 10b) - (3a + 4b)
Rewrite subtraction as adding
the opposite.
(7a - 10b) + (- 3a - 4b)
Group the like terms.
7a - 3a - 10b - 4b
4a - 14b
6. Subtract the following
polynomials using column form:
(4x2 - 2xy + 3y2) - (-3x2 - xy + 2y2)
Line up your like terms and add the
opposite.
4x2 - 2xy + 3y2
+ (+ 3x2 + xy - 2y2)
--------------------------------------
7x2 - xy + y2
Add or Subtract
Polynomials
1.
(5y2 – 3y + 8) + (4y2 – 9)
Answer: 9y2 –3y –1
2.
(3ax2 – 5x – 3a) – (6a – 8a2x + 4x)
Answer: 3ax2 – 9x – 9a + 8a2x
Find the sum or difference.
(5a – 3b) + (2a + 6b)
1.
2.
3.
4.
3a – 9b
3a + 3b
7a + 3b
7a – 3b
Find the sum or difference.
(5a – 3b) – (2a + 6b)
1.
2.
3.
4.
3a – 9b
3a + 3b
7a + 3b
7a – 9b
Multiplying Polynomials
Multiplying a
Polynomial by a
Monomial
Examples
1. -2x2(3x2 – 7x + 10)
 Notice the –2x2 on the outside of the
parenthesis……you must distribute this.
 -2x2 * 3x2 = -6x4
 -2x2 * -7x = 14x3
 -2x2 * 10 = -20x2
 Answer: -6x4 + 14x3 – 20x2
Examples
2. 4(3d2 + 5d) – d(d2 –7d + 12)
 Notice you have to distribute the 4 and –d
 4 * 3d2 = 12d2
 4 * 5d = 20d
 -d * d2 = -d3
 -d * -7d = 7d2
 -d * 12 = -12d
 Put it all together….
 12d2 + 20d –d3 + 7d2 – 12d
 Notice the like terms….
 Answer: -d3 + 19d2 + 8d
Multiplying Two Binomials
 Example:
 (x + 3) (x + 2)
 This can be done a number of ways.
 Use either FOIL or Box Method
FOIL
 (x + 3) (x + 2)
 F-Multiply the First terms in each
 x * x = x2
 O-Multiply the Outer terms
 x * 2 = 2x
 I-Multiply the Inner terms
 3 * x = 3x
 L-Multiply the Last terms
 3*2=6
 Answer: x2 + 5x + 6
Box Method
Combine
 Add the two that are circled
 Answer:
 x2 + 5x + 6
Polynomials
(4x + 9) (2x2 – 5x + 3)
 Multiply 4x by
(2x2 –5x + 3)
 4x *
2x2
=
8x3
 4x * -5x = -20x2
 4x * 3 = 12x
 Multiply 9 by
 9 * 2x2 = 18x2
 9 * -5x = -45x
 9 * 3 = 27
(2x2 –5x + 3)
Put it all Together
 8x3 – 20x2 + 12x + 18x2 –45x + 27
 Now combine like terms
 Answer:
 8x3 –2x2 –33x + 27
Special Products
 A. Square of a Sum: The square of a + b is the

square of a plus twice the product of a and b plus

the square of b.

Symbols: (a + b)² = (a + b)(a + b)

= a² + 2ab + b²

Example: (x + 7)² = x² + 2(x)(7) + 7²

= x² + 14x + 49
 Find each product:
 1). (4y + 5)²
2). (8c + 3d)²
 B. Square of Difference: The square of a – b is the

square of a minus twice the product of a and b

plus the square of b.

Symbols: (a – b)² = (a – b)(a – b)

= a² - 2ab + b²

Example: (x – 4)² = x² - 2(x)(4) + 4²

= x² - 8x + 16
 Find each product:
 1). (6p – 1)²
2). (5m³ - 2n)²
 C. Product of a sum and a difference: The product

of a + b and a – b is the square of a minus the

square of b.

Symbols: (a + b)(a – b) = (a – b)(a + b)

= a² - b²

Example: (x + 9)(x – 9) = x² - 9²

= x² - 81
 Find each product:
 1). (3n + 2)(3n – 2)
2). (11v – 8w²)(11v + 8w²)
Summary:
 Square of a Sum………(a + b)² = a² + 2ab +b²
 Square of a Difference…(a – b)² = a² - 2ab +b²
 Product of a Sum and a Difference …………….(a – b)(a + b) = a² - b²
Guided Practice:
 1. (a + 6)²
2. (4n – 3)(4n – 3)
 3. (8x – 5)(8x + 5)
4. (3a + 7b)(3a – 7b)
 5. (x² - 6y)²
6. (9 – p)²
7. (p + 3)(p – 4)(p – 3)(p + 4)
Examples
3. y(y – 12) + y(y + 2) + 25 = 2y(y + 5) – 15
 Distribute y, y and 2y
 y * y = y2
 y * -12 = -12y
 y * y = y2
 y * 2 = 2y
 Don’t forget the +25
 2y * y = 2y2
 2y * 5 = 10y
 Don’t forget the -15
 Now you have…….
 y2 – 12y + y2 + 2y + 25 = 2y2 + 10y –15
 Combine like terms….
 2y2 –10y + 25 = 2y2 + 10y – 15
 Now you have to solve because you have an equals sign
 Answer: y = 2