Download 2e614d5997dbffe

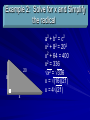
‫‪Pythagorean Theorem‬‬
‫إعداد الطالب ‪:‬‬
‫شهاب فؤاد عبد المنعم صبرى‬
‫الصف األول اإلعدادى‬
‫تحت إشراف ‪:‬‬
‫أ ‪ /‬تامر‬
Pythagorean Theorem
Objectives:
1) To use the Pythagorean Thm.
2) To use the converse of the Pythagorean Thm.
The Pythagorean Theorem is one of the most famous
theorems in mathematics. The relationship it describes
has been known for thousands of years.
Pythagoras (~580-500 B.C.)
He was a Greek philosopher responsible for important
developments in mathematics, astronomy and the theory of
music.
President Garfield may have been joking when he stated about his
proof that, "we think it something on which the members of both
houses can unite without distinction of the party." A nice feature of
mathematical proofs is that they are not subject to political opinion.
PROVING THE PYTHAGOREAN THEOREM
THEOREM
THEOREM 8-1 Pythagorean Theorem
In a right triangle, the
square of the length
of the hypotenuse is
equal to the sum of
the squares of the
lengths of the legs.
c
a
b
c2 = a2 + b2
(Converse is Theorem 8-2)
Pythagorean Theorem
** Only works for rt. Δs
a2 + b 2 = c 2
Legs
c
a
Legs
b
* Sides that form the right 
Hyp
Example 1: Find the missing side
of the Δ.
a2 + b2 = c2
212 + 202 = x2
x
21
441 + 400 = x2
841 = x2
20
√841 = √x2
29 = x
Pythagorean Triple – Is a set of
nonzero whole numbers that satisfy
the equation: a2 + b2 = c2
Examples: 3, 4, 5
6,8,10
15,20,25 …
5, 12, 13
8, 15, 17
7, 24, 25
** Multiply each number in a pyth. Triple by the same
whole number then the resulting numbers are pyth.
Triples also.
Math Review
Perfect Squares
–
–
–
–
–
–
–
–
–
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
Radicals
√3 • √3 = √9 = 3
√40 = √4 • 10 = 2√10
√80 = √4•20 = 2√4•5
= 2•2√5 = 4√5
Example 2: Solve for x and Simplify
the radical
20
8
x
a2 + b2 = c2
x2 + 82 = 202
x2 + 64 = 400
x2 = 336
√x2 = √336
x = √(16)(21)
x = 4√(21)
Example 3: Find the area of ΔDCE
D
a 2 + b2 = c2
102 + b2 = 122
12m
12m
100 + b2 = 144
b2 = 44
E
C
b = √44
A = ½ bh
20m
= ½ (20m)(6.6m)
= 66m2
b = √(4)(11)
b = 2√(11)
b = 6.6m
Example 4: Are the following Δs, rt. Δ
a2 + b2 = c2
85
13
842 + 132 = 852
7056 + 169 = 7225
7225 = 7225
YESS!
84
a2 + b2 = c2
50
16
482 + 162 = 502
2304 + 256 = 2500
48
2560 ≠ 2500
Nope!
Non-Right Δs
Th(8-3) If the square of the length of the
longest side of a Δ is greater than the sum
of the squares of the lengths of the other 2
sides, the Δ is obtuse.
2
If a
+
2
b
is obtuse.
<
2
c , then the Δ
Th(8-4) If the square of the length of the
longest side of a Δ is less than the sum of
the squares of the lengths of the other 2
sides, then the Δ is acute.
2
If a
+
is acute.
2
b
>
2
c , then the Δ
Is the Δ Right, Obtuse, or Acute?
Ex. 5
Sides of 6, 11, 14
Ex. 6
Sides of 15, 13, 12
a2 + b2 = c 2
62 + 112 =142
36 + 121 = 196
157 < 196
Obtuse
a2 + b 2 = c 2
122 + 132 =152
144 + 169 = 225
313 > 225
Acute
Ex. 7 Find AC and BC
A = ½ bh
The area of ΔABC is 20ft2
C
20ft2 = ½ (10ft)h
h=4
To find AC
hh
a2 + b2 = c2
A
2ft
8ft
To find BC
a2 + b2 = c2
42 + 82 =BC2
16 + 64 = BC2
80 = BC2
BC = √16 • 5
BC = 4√5
B
22 + 42 = AC2
4 + 16 = AC2
AC = √20
AC = √4•5
AC = 2√5
Day 1
page 420, 1-17 all
Day 2
page 420, 18-29, 36,39,40,44