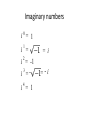Download LOGARITHMS,MATRICES and COMPLEX NUMBERS

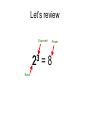
LOGARITHMS,MATRICES
and COMPLEX NUMBERS
By
Maurice Fritz and Karen Greer
Let’s review
Exponent
3
2
Base
Power
=8
What do you know about
logarithms?
WHEN WE ARE GIVEN the base 2, for example, and exponent 3, then
we can evaluate 23.
8
23 = ?
On the other hand, IF WE ARE GIVEN, the base 2 and its power 8 –
2? = 8
-- then what is the exponent that will produce 8?
That unknown exponent is called a logarithm.
We call the exponent 3 the logarithm of 8 with base 2. We
write
3 = log28.
EXPONENTIAL TO LOGARITHM
The exponential equation 23 = 8 could be written in terms of a logarithmic equation
as log2 8 = 3 .
3
23 =
2
8
log
which we say “log-base-2 of 8 equals 3”.
More about logarithm:
Given: log 100. Since there is no subscript
the base of 10 is automatically assumed.
Therefore log 10100 is 2.
Multiplication is a shortcut for addition. For example: 3x5 means 5 + 5 + 5.
Exponents are a shortcut for multiplication with the same number. For example:
2x2x2 means 23 .
Logarithm is a shortcut for exponents.
Just as subtraction is the opposite of addition and division is the opposite of
multiplication,
Logarithms are the "opposite" of exponentials.
Let’s do some conversion examples
Convert 63 = 216 to the equivalent logarithmic expression.
Convert 33 = 27 to the equivalent logarithmic expression.
Solve: log5 25 = y.
5 to what exponent produces 25?
The required power is 2, because 52 = 25. Then 52 = 5 y = 25, so:
log5(25) = 2; therefore, y = 2
Solve: log6 36 = y.
Solve: log2 32 = x.
Solve: log8 1 = x.
Solve: log7 7 = x.
The three laws of logarithms
1. logb xy = logb x + logb y
“The logarithm of a product is equal to the sum of the logarithms of
each factor.”
2. logb x = log x - log y
b
b
y
“The logarithm of a quotient is equal to the logarithm of the numerator
minus the logarithm of the denominator.”
3.
logb xn = n logb x
“The logarithm of a power of x is equal to the exponent of that power
times the logarithm of x.”
logbxy = logbx + logby
log7 9y = log7 9 + log7 y
log3 (2xy) = log3 2 + log3 x + log3 y
logb x = log x - log y
b
b
y
log3 2 = log 2 - log y
3
3
y
log7 3 = log 3 - log 5
7
7
5
logb xn = n logbx
log2 x9 = 9 log2x
log7 25 = 5 log7 2
log5 3 x9y = log 3 + log x9 + log y - log z
5
5
5
5
z
= log5 3 + 9 log5 x + log5 y - log5 z
What are applications of logarithms?
• 1. Logarithms are used in applications which are related to hearing
because we hear with our ears in a logarithmic relation.
This also has to do with equipment with decibel ratings because of
how we hear.
• 2. Logarithms have been used for slide rules when multiplication
and division are performed.
When we perform slide rule addition, it is like the product rule for
logarithms and results in multiplication. When we perform slide rule
subtraction, it is like the quotient rule for logarithms and results in
division.
In mathematics, a matrix (plural matrices) is a rectangular two-dimensional
group of numbers, such as
4 0
A 3 7
6 -1
-2 5
7
6
0
2
An item in a matrix is called an entry or an element.
The dimension of a Matrix
column
column
column
4 0 7
A 3 7 6
6 -1 0
-2 5 2
row
row
row
row
This matrix A has four rows and three columns.
We say it is a 4 by 3 matrix.
It is written as 4 X 3 matrix.
Rows x Columns
Operations with Matrices
4 -1 0
A
8 2 6
B
-2 5 3
-1 3 0
To add matrices just add the corresponding elements, the
matrices being added must have the same dimensions.
Find A + B
Find A B
Operations with Matrices
4 -1 0
A
-2 5 3
8 2 6
B 1 2 1
-1 3 2
The product of two matrices is found by multiplying the
elements of the rows of the matrix on the left by the
corresponding elements of the columns of the matrix on the
right. The resulting matrix must have the same column of the
first one and row of the second one for the first row and the
same row of the first one and column of the second for the
second row.
Find AB
Determinants
A determinant is also an ordered array of
numbers within rectangular brackets and has a
lot of similarities to a matrix.
The most useful application of determinants is in
solving linear Algebraic equations.
Solution of a 2 by 2 determinant
For a 2×2 matrix, its determinant is found by
subtracting the products of its diagonals.
Find a b = ad - bc
c d
Example: Find the following determinant.
Find 2 6 = (2)(5) - (6)(7) = 10 – 42 = -32
7 5
Cramers Rule for 2 by 2 Systems
•
•
•
•
•
•
•
•
•
•
•
This rule solves linear systems using
determinants. Given the system
a1 x + b1y = c1 and
a2x + b2y = c2
We need 3 determinants as follow to solve
this. D = a1 b1 Dx = c1 b1 Dy = a1 c1
a2 b2
c2 b2
a2 c2
where c1 and c2 replace a1 and a2 in Dx
and c1 and c2 replace b1 and b2 in Dy.
The solution is x = Dx and y = Dy.
D
D
• Solve the following system using Cramer’s Rule and the
necessary determinants.
• 2x - 3y = 2
• 5x + y = 22
• Determinant D = 2 -3 = 2(1) –(-3)(5) = 17
•
5 1
• Determinant Dx = 2 -3 = 2(1) –(-3)22 =68
•
22 1
• Determinant Dy = 2 2 = 2(22) -5(2) = 34
•
5 22
• X = Dx/D = 68/17 = 4 y = Dy/D = 34/17 = 2
• Check 2(4) -3(2) = 8-6 = 2 5(4) + (1)2 = 20 +2 =22
•
•
•
•
•
•
•
•
•
•
•
•
•
Now lets practice what we have learned
on some exercises with matrices and
Determinants.
1 _______(A) True, (B) False. You can
add a 2 by 3 matrix and a 3 by 4 matrix.
2 Given A = 5 -4 7 and B = 7 8 -2
6 2 -3
4 9 1
Find A + B
3 Given A = 3 4 2
and B = -6 4
5 0 4
2 3
3 -2
Find the product AB
4 Find (a) D, (b) Dx,( c) Dy,(d) x and (e)y.
• for these 2 equations 3x + 2y = 9
•
7x - y = 4
We don’t have a real number solution to this.
So we say,
=i
And we call
i
an
Imaginary number
Imaginary numbers
0
i =
1
1
i =
2
i = -1
3
i =-
4
i =
1
=i
= -i
Imaginary numbers Continues
0
i =1
1
i =
2
i =
i
-1
15
4
i = i i 4 i 4 i 33 = i 3 = - i
111i
3 R3
4 15
38
i = i2=-1
9 R2
4 38
3
i =-i
4
i =
1
COMPLEX NUMBERS
What do you know about complex numbers?
A complex number is a number consisting of a
real part and an imaginary part.
i
3+7
ADDING COMPLEX NUMBERS
• Example 1 Add A = (2 + 3i) + B = (5 + 4i).
• Add the real parts and the imaginary parts to get
(2 + 5) + (3 + 4) i = 7 + 7i
• Example 2 Add A = (4 + 2i) + B = (3 -5i).
• (4 + 3) + (2 -5)i = 7 – 3i
• MULTIPLYING COMPLEX NUMBERS
• Multiply 3i(4 + 2i) = 3(4)i + (3)(2)i2
• Since i2 = -1, then we get 12i + 6(-1) =
• -6 + 12i.
A PRACTICAL APPLICATION OF
COMPLEX NUMBERS
• Complex numbers are used in electrical
• and electronic circuits. The real part is the
• resistive component. The imaginary parts
are inductors which are +i and
• capacitors which are -i.
• Example: A 10 ohm resistor, a 15 ohm
• inductor and a 20 ohm capacitor are
placed in a series circuit.
• In a series circuit the complex number
values need to be added. Find the
• resulting complex number value.
• 10 + 15i -20i = 10 -5i.
• The result is 10 ohms resistive + 5 ohms
• capacitive.
COMPLEX NUMBER EXERCISES
•
•
•
•
•
•
•
•
1
2
3
4
Find (a) i12 and (b) i23.
Add = (3 + 4i) + (2 -7i).
Multiply = 6i(4 -5i).
A 20 ohm resistor, a 30 ohm inductor
and a 10 ohm capacitor are placed in
a series circuit. Find the resulting
complex number value. Is it resistive
and inductive or resistive and capcitive?