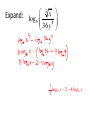Download Unit V: Properties of Logarithms

5.0
Properties of Logarithms
AB Review for Ch.5
Rules of Logarithms
If M and N are positive real numbers and b is ≠ 1:
•
The Product Rule:
•
logbMN = logbM + logbN
(The logarithm of a product is the sum of the logarithms)
•
•
Example: log4(7 • 9) = log47 + log49
Example: log (10x) = log10 + log x
Rules of Logarithms
If M and N are positive real numbers and b ≠ 1:
•
The Product Rule:
•
logbMN = logbM + logbN
(The logarithm of a product is the sum of the logarithms)
•
•
•
•
Example: log4(7 • 9) = log47 + log49
Example: log (10x) = log10 + log x
You do: log8(13 • 9) = log813 + log89
You do: log7(1000x) = log71000 + log7x
Rules of Logarithms
If M and N are positive real numbers and b ≠ 1:
•
The Quotient Rule
M 
logb    logb M  logb N
N
(The logarithm of a quotient is the difference of the logs)
•
Example:
x
log    log x  log 2
2
Rules of Logarithms
If M and N are positive real numbers and b ≠ 1:
•
The Quotient Rule
M 
logb    logb M  logb N
N
(The logarithm of a quotient is the difference of the logs)
•
Example:
x
log    log x  log 2
2
•
You do:
 14 
log 7   
 x
log7 14  log7 x
Rules of Logarithms
If M and N are positive real numbers, b ≠ 1, and p is any real
number:
• The Power Rule:
• logbMp = p logbM
(The log of a number with an exponent is the product of the
exponent and the log of that number)
• Example: log x2 = 2 log x
• Example: ln 74 = 4 ln 7
9log35
• You do: log359 =
ln
x
Simplifying (using Properties)
• log94 + log96 = log9(4 • 6) = log924
• log 146 = 6log 14
3
• log
a 3  log 2  log
2
log163
• You try: log1636 - log1612 =
• You try: log316 + log24 =
• You try: log 45 - 2 log 3 =
Impossible!
log 5
Using Properties to Expand Logarithmic
Expressions
• Expand: log x 2 y
b
notation
log b
1
2 2
x y
log b x  log b
2
Use exponential
1
y2
1
2 log b x  log b y
2
Use the product rule
Use the power rule
Expand:
 3 x
log 6 
4
 36 y



1
log 6 x  2  4 log 6 y
3
Condense:
logb M  logb N  3logb P
MN
log b 3
P
Change of Base
• Examine the following problems:
• log464 = x
» we know that x = 3 because 43 = 64, and the base of this
logarithm is 4
• log 100 = x
– If no base is written, it is assumed to be base 10
» We know that x = 2 because 102 = 100
• But because calculators are written in base 10,
we must change the base to base 10 in order
to use them.
Change of Base Formula
logM
logb M 
logb
• Example log58 =
log 8
 12900
.
log 5
• This is also how you graph in another base. Enter
y1=log(8)/log(5). Remember, you don’t have to
enter the base when you’re in base 10!
Graphing logarithmic functions
Find the domain, vertical asymptotes, and x-intercept.
Sketch a graph.
f  x   log6 x
y
x
Domain :  0,  
4
VA : x  0
x  int : 1,0
–4
13
Graphing logarithmic functions.
Find the domain, vertical asymptotes, and x-intercept.
Sketch a graph.
g  x   log10  x 1  4
y
Domain : 1,  
x
4
VA : x  1
x  int : 1  104 , 0 
–4
Homework:
MMM pg. 186-188