* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download have shown no evidence
Radioactive decay wikipedia , lookup
Nuclear fusion–fission hybrid wikipedia , lookup
Nuclear fission wikipedia , lookup
Nuclear transmutation wikipedia , lookup
Nuclear fusion wikipedia , lookup
Nuclear binding energy wikipedia , lookup
Valley of stability wikipedia , lookup
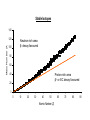
Radiochemistry Dr Nick Evans [email protected] Why Radiochemistry? Radioisotopes are widely used in: 1. Diagnostic and therapeutic nuclear medicine 2. 3. 4. 5. • 500 000 per annum Mechanistic and kinetic studies of reactions Analysis Agriculture Industry Why? 1. Ease and sensitivity of detection of radioisotopes 2. Automation of counting of radioisotopes 3. Availability of radioisotopes Theory of Atomic Structure • Atom = nucleus + extra-nuclear electrons • Nucleus = neutrons and protons held together by “strong interactions” • Strong nuclear force (interaction) is a fundamental force of nature which affects only quarks, antiquarks, and gluons • Range of force is about 10-15 m • Strong enough to overcome Coulombic repulsion of protons Potential Energy of Proton near Nucleus PE Coulombic Repulsion 0 Distance from nucleus (r) Range of attractive Nuclear Force Binding Energy of Nucleus • Indication of how strongly the nucleus is bound together • Energy liberated in formation of nucleus from its nucleons is a measure of its stability • High binding energy = stable nucleus • Sum of individual masses of nucleons is different 16 O to mass of nucleus, e.g. for 8 Binding Energy of Nucleus (2) • On 12C scale: – Mass of proton – Mass of neutron – Mass of electron = 1.007825 amu = 1.008665 amu = 0.0005485 amu • Thus: – – – – 8 protons 8 neutrons 8 electrons Sum = = = = 8.0626 8.06932 0.004388 16.136308 • Actual mass of 16O on 12C scale = 15.9949148 • Therefore, mass defect = 0.141394 amu Binding Energy of Nucleus (3) • Decrease in mass is due to energy release when atom is formed, i.e.: • E = mc2 = 0.141394 x 10-3 kg x (3 x 108 ms-1)2/6.023 x 1023 = 2.1128 x 10-11 J • But 1 eV = 1.6021 x 10-19 J • Thus E = 131.9 MeV or = 8.24 MeV per nucleon • Sun loses 4.2 million tonnes per second as it builds heavier nuclei • Plot binding energy per nucleon vs. mass number Binding Energy per Nucleon vs. Mass Number Binding Energy per Nucleon (MeV) 9 8 7 Fusion releases energy 6 Fission releases energy 5 0 50 100 150 Mass Number 200 250 Binding Energy per Nucleon • The most stable elements have mass numbers around 56, specifically 56 Fe 26 • 8 MeV is high energy compared with electromagnetic radiation – UV is a few electron volts (eV) to ~100 eV – X-ray photons have energies ~100 eV to ~100 keV – Gamma-ray energies > 100 keV • Small peaks represent particularly stable nuclei – high binding energy per nucleon 4 2 He, 16 8 O, 28 14 Si, 42 20 Ca, 88 38 Sr, 208 82 Pb etc. Separation Energy • Energy required to remove a single neutron from the nucleus • Shows the stability of nuclei built from α-particles • Mass increasing in jumps of 4 Neutron Separation Energies 28 Si-28 26 24 Neutron Separation Energy (MeV) 22 20 He-4 Be-8 18 C-12 Ne-20 16 Mg-24 O-16 S-32 14 12 B-11 N-14N-15 10 Al-26 Ne-22 Mg-25 Ne-21 Li-6 C-13 4 2 P-31 P-30 Si-29 Li-7 6 O-17 Be-9 0 -2 0 F-19 F-18 B-10 8 Al-27 Na-23 2 He-5 4 6 8 10 12 14 16 18 Atomic Number 20 22 24 26 28 30 32 Magic Numbers • Leads to concept of ‘magic numbers’ for certain numbers of neutrons and protons • Suggests there are energy levels in the nucleus • Equivalent to idea of full outer shell of electrons in noble gases • Magic Nos.: 2, 8, 20, 28, 50, 82, 126 • Nuclei with this number of protons, or neutrons or sum of the 2 which is a magic number are especially stable, e.g. 4 He, 16 O, 40 Ca, 208 Pb 2 8 20 82 Nuclear Energy Levels Two Theories of Nuclear Structure: • Liquid drop model • Assumes nucleons behave like molecules in a liquid • random movement and exchange of position • Scattering experiments suggest that nuclei have approximately constant density (2.4 x 1014 g cm-3) • Takes into account that the forces on nucleons on surface are different from those in interior where the nucleons are completely surrounded by others • Like taking into account surface tension of liquid drop Nuclear Energy Levels (2) • Shell Model • Accounts for energies of particles emitted • Dense-gas type models of nuclei with multiple collisions between particles didn't fit data • Patterns like magic numbers suggest shell structure Nuclear Energy Levels • Analogous to filled electron shells • No principal quantum number • Levels are determined by angular momentum quantum number • Jumps between levels caused by absorption or emission of energy • Often gamma Neutron : Proton Ratio • Approximately 275 nuclei have shown no evidence of radioactive decay • ~60% of these have: • even numbers of protons and • even numbers of neutrons • In general the most abundant on earth • Remaining ~40% are about equally divided between: • even number of protons and odd number of neutrons • odd number of protons and even number of neutrons Neutron : Proton Ratio (2) • There are only 4 ‘stable’ nuclei with an odd number of protons and neutrons: • 2 6 Li, 10 B, 14 N, H, 1 3 5 7 • Relative abundances of 0.015, 7.42, 19.6, 99.63% • Very light nuclei • Elements of even atomic number have more stable isotopes than those of odd atomic number • Occurs due to energy stabilisation of pairs of protons and/or neutrons The Stable Region • Stability is favoured by even numbers of protons and neutrons • Not usually equal numbers • Plotting neutron number (A) against proton number (Z) for all known nuclei, shows area of stability • For very light elements N ≈ Z gives stable elements • 1:1 up to 4020Ca • Ratio gradually rises (A>Z) until by element 83 (Bi, the last one with a stable isotope) it is ~1.5 The Stable Region (2) • If the N/P ratio is too high for stability then isotope is neutron rich • likely to decay by β- emission • If the N/P ratio is too low for stability then isotope is proton rich • likely to decay by β+ emission or electron capture Stable Isotopes 140 Mass Number (A) 120 Neutron-rich area β- decay favoured 100 80 60 40 Proton-rich area β+ or EC decay favoured 20 0 0 10 20 30 40 50 Atomic Number (Z) 60 70 80 90 Nuclei Showing Ground State Energy (MeV) 61Zn 62Zn 63Zn 64Zn 65Zn 56765 57692 58623 59550 60482 60Cu 61Cu 62Cu 63Cu 64Cu 55832 56760 57690 58619 59551 59Ni 60Ni 61Ni 62Ni 63Ni 54898 55826 56758 57686 58619 58Co 59Co 60Co 61Co 62Co 53967 54896 55829 56759 57692 57Fe 58Fe 59Fe 60Fe 61Fe 53036 53965 54898 55829 56763 Stable Isotopes 61Zn 62Zn 63Zn 64Zn 65Zn 56765 57692 58623 59550 60482 60Cu 61Cu 62Cu 63Cu 64Cu 55832 56760 57690 58619 59551 59Ni 60Ni 61Ni 62Ni 63Ni 54898 55826 56758 57686 58619 58Co 59Co 60Co 61Co 62Co 53967 54896 55829 56759 57692 57Fe 58Fe 59Fe 60Fe 61Fe 53036 53965 54898 55829 56763 Mass = 61 Isobar Mass Difference (MeV) 10 8 Fe 6 Zn 4 Co 2 Cu 0 Ni -2 25 26 27 28 29 30 31 Atomic Number Normally only 1 nucleus per mass number is stable