Download Maths revision File

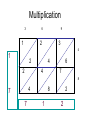
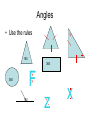
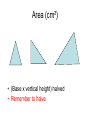
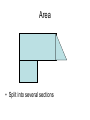
Maths revision
What maths can be used in the question?
What strategies will help?
What working do I need to show?
Is the answer down to maths?
Number
• Integers = whole numbers
• Prime numbers = cannot be ÷ by any
number except itself (2, 3, 5, 7, 11, etc)
• Multiple = in that numbers times table
• Factor = a number that ÷ into it
• Square number = the result of a number x
itself (1, 4, 9, 16, etc)
• Square root is the opposite of square
Approximations
• Sometimes an answer is too precise and
needs rounding off.
e.g. 7.88889934 pence would make more
sense to be written as 8p
Basically if the number is 5 or larger the
previous number rounds up.
E.g. 6.547 could be written as 7 or 6.5 or 6.55
Decimal places and significant
figures
• These are instructions into how precise the
answer must be.
Decimal places start from the point.
E.g.237.664 = 237.7 to 1 decimal place
or = 237.66 to 2 decimal places
Significant figures start at the first number
E.g. 237.664 = 200 to 1 significant figure
or = 240 to 2 significant figures
Multiplication
3
6
1
9
2
3
4
1
2
2
4
4
6
7
8
4
7
7
8
1
2
2
Decimals
• 0.2 = 2/10 = 1/5
(20p)
• 0.02 = 2/100 = 1/50 (2p)
• If 3 x 4 = 12
Then 0.3 x 4 = 1.2
And 30.0 x 0.4 = 12
And 0.3 x 0.4 = 0.12
etc.
Fractions
• 2 ¼ = 9/4 (4 x 2 + 1 = 9 quarters)
• 3 4 = 34 (3 x 10 + 4 = 34 tenths)
10
• 12
18
10
=
6
9
=
2
3
( cancel by other numbers than 2)
Fractions 2
• The method for + and – is the same
• 3 - 2
4 3
X3
(think 3 x 4)
X4
9
12
8
12
Include the red arrow
9–8= 1
12
Fractions 3
• Multiply is easy
• 2 x 4 = 8
• 3
5 15
• Divide is easy if you turn the 2nd upside
down
• 2 ÷ 4 becomes 2 x 5 = 10 = 5
3 5
3
4
12
6
Fractions 4
To find three quarters (3/4) of a number (32)
1 32 ÷ 4 = 8
2 8 x 3 = 24
Three quarters of 32 is 24.
Percentages
• With a calculator
1 ÷ by 100
2 X by the %
e.g. find 22% of 600
600 ÷ 100 = 6
6 x 22 = 132
Percentages
•
1
2
3
Without a calculator
Find 10% move the decimal point 1 place
Find 1% move the decimal point 2 places
Use these to get to the answer
e.g. find 22% of 600
10% = 60.0 and 1% = 6.00
So 22% = 60 + 60 + 6 + 6 = 132
Writing as a percentage
• First write as a fraction
• Then x by 100
• E.g. A car is bought for £10,000 and sold
for £8,000. what is the percentage loss?
loss = 2,000 x 100 = 2000 = 20%
10,000
100
Fractions/Decimals/Percentages
• To compare change them all to %
E.g. Arrange 0.61, 3/5, 59%, 0.599 in order
0.61 = 61 out of 100 = 61%
3/5 of 100 = 60%
0.599 is 59 and a bit out of 100 = 59.9%
So 59% then 0.599, then 3/5, then 0.61
Negative numbers
Go up and down a ladder
-3 -3 = -6,
-3 +2 -2 = -3
7 -4 -5 = -2
7 -4 +1 = 4
BUT if there are 2 signs next to each other.
-3 - -3 = -3 +3 = 0
7 + -2 + +4 - -5 = 7 -2 +4 +5 = 14
Simplify the signs BEFORE using a ladder
Negative numbers
• Multiplying/dividing/brackets involve the
signs coming together
-3 x -3 is 3 x 3 and - - = +9
5 x -2 is 5 x 2 and + - = -10
-10 = +2
-5
12 = -2
-6
-3(-5) = +15
(-4)² = -4 x -4 = +16
Angles
• Use the rules
180
360
F
360
180
z
x
Ratios
• Bill and Ben share £30 in the ratio of 3:2
• This means that the money is being
shared 5 ways
• The key is to find the value of 1 share
£30 ÷ 5 = £6 = 1 share
Bill gets £6 x 3 = £18
Ben gets £6 x 2 = £12
Area (cm²)
• (Base x vertical height) halved
• Remember to halve
Area
• Split into several sections
Area
• Base x vertical height
Circles
Volume (cm³)
• Volume = area of A x length l
A
l
A
l
A
l
Probability
• Probabilities are expressed in decimals or
fractions.
• Probabilities lie between 0 (not possible)
and 1 (must happen)
• What is the probability of choosing an 8 in
a pack of cards
• Answer 4 in 52 or 1/13
Relative frequency
• Relative frequency is the number of times that
the event is likely to happen
• e.g. a RF of 0.2 means it will happen one fifth of
the time.
• How many times will the red counter appear in
200 goes if the relative frequency is 0.3
• Answer 0.3 x 200 = 60
• The relative frequency can be found by
experimenting but to be reasonably accurate
must be found after numerous goes.
Algebra - simplifying
• Similar terms can be added or subtracted.
• a + 3a = 4a
5y – 2y = 3a
BUT 3y – 2a cannot be simplified
Simplify 3a – 4y + 2y – 5a + 8y
Answer -2a + 6y or 6y – 2a
Algebra - simplifying
• Multiplying
2a x 3b = 6ab
2a x -4a x 3c = -24a²c
Dividing
6a ÷ 3a = 2
10a²bd = 2ad
5ab
Think number/letter/sign
10a ÷ 5c = 2a/c
Algebra - solving
• Get rid of brackets
• Isolate the unknowns on one side
• Find the value of the unknown
5(a – 2) = 3(a + 6) don’t forget the number
5a – 10 = 3a + 18
5a – 3a =
+18 +10 change the signs
2a
= 28 find the value of 1
a
= 14