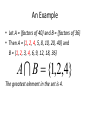Download Section 4.3

MTH 231
Section 4.3
Greatest Common Divisors and Least
Common Multiples
Overview
• We now come to a critical stage in student
development.
• It is critical because the two concepts in the
section are foundations of fraction arithmetic:
1. Greatest common divisors are used to reduce
fractions to lowest terms;
2. Least common multiples are also least
common divisors, which are needed to add
or subtract fractions.
Greatest Common Divisor
• Let a and b be whole numbers. The greatest
natural number d that divides both a and b is
called their greatest common divisor (or
greatest common factor):
d  GCD(a, b)  GCF (a, b)
Finding the GCD (or GCF)
Method 1: Intersection of Sets
• Good to use when the numbers involved are
small and all the factors of each number are
easily written down.
• Can be modeled using Venn Diagrams
An Example
• Let A = {factors of 40} and B = {factors of 36}
• Then A = {1, 2, 4, 5, 8, 10, 20, 40} and
B = {1, 2, 3, 4, 6, 9, 12, 18, 36}
A  B  {1,2,4}
The greatest element in the set is 4.
Using Venn Diagrams
Finding the GCD (or GCF)
Method 2: Prime Factorizations (with and
without exponents)
• Utilizes and reinforces prime factorization
(listed or using factor trees)
• Exponential form can be used with older
students (common prime factors to the
smallest exponent)
An Example: Using Prime Factors
Find the GCD of 24 and 40.
24 = 2 x 2 x 2 x 3
40 = 2 x 2 x 2 x 5
GCD(24,40) = 2 x 2 x 2 = 8
Using a Factor Tree
Using Prime Factors with Exponents
24 = 23 x 31
40 = 23 x 51
GCD(24,40) = 23 = 8
An Application of GCD
• Sally’s class collected jeans, shirts, and socks
for a clothing drive. They want to fill bags with
jeans, shirts, and socks so that each bag has
the same number of each item. If the class
collected 12 pairs of jeans, 18 shirts, and 24
pairs of socks, what is the largest number of
bags the class can make?
Least Common Multiple
• Let a and b be natural numbers. The least
natural number m that is a multiple of both a
and b is called their least common multiple:
m  LCM (a, b)
Finding the LCM
Method 1: Intersection of Sets
• Simple, works well if the two numbers are not
large.
• Does not necessarily model well using Venn
Diagrams but can be modeled using the
number line.
• Note: for numbers that are co-prime, the LCM
is the product of the numbers.
An Example
Finding the LCM
Method 2: Prime Factorization
• Use prime factorization to write each number
as a product of prime factors (with or without
exponents)
• List all the factors in both numbers. For
common factors, use the larger exponent.
• Multiply. This result will be your LCM.
An Example
63 = 32 x 71
120 = 23 x 31 x 51
LCM(63,120) = 23 x 32 x 51 x 71 = 2520
An Application of LCM
• Sally’s class is having a Halloween party. They plan to
serve hot dogs. If hot dogs are sold in packages of 10,
and hot dog buns are sold in packages of 8, what is
the smallest number of buns they should buy so that
all the hot dogs and buns are used?
• Sally cleans her closet every 4 days and vacuums her
room every 5 days. On November 1, she does both.
On what day will she do both again?