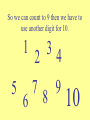Download Xmania! - MathinScience.info

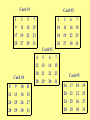
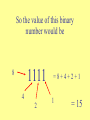
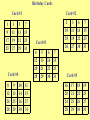
Count on
it
What day is your birthday?
Think of the DATE you were born,
but don’t say it out loud!
Card #1
Card #2
1
9
17
3
11
19
5
13
21
7
15
23
2
10
18
3
11
19
6 7
14 15
22 23
25
27
29
31
26
27
30 31
Card #3
Card #4
4
5
6
7
12
20
28
13
21
29
14
22
30
15
23
31
Card #5
8
9
10
11
16
17
18
19
12
24
28
13
25
29
14
26
30
15
27
31
20
24
28
21
25
29
22
26
30
23
27
31
What to expect…
• Learn some new things about our number
system.
• Learn some stuff about other number
systems.
• Learn some cool short-cuts that work for
our number system.
• Learn how the Birthday cards work.
Let’s look at what we know:
• How many digits are
there? 10 digits
• How many numbers are
there? ∞ (infinity)
• Do we have to use 1,2,3…
or can we use something
else? Any symbol will work.
• Do we know any other
number systems?
Yes!
• When is 8 + 5 = 1?
On a Clock!
So what is the value of --
34
Why is it not 7?
So we can count to 9 then we have to
use another digit for 10.
1
34
2
5 7 8 9
6
10
Back in the day…
• Different groups used
different symbols.
• Symbols could be a
single value or different
values (depending on
where they were).
• Here’s some examples:
Here’s a few the Egyptians used
So what’s their value?
© Mark Millmore 1997 - 2004
A Few Mayan Math Symbols
In Mayan Math
This is 1
This is 2
The Mayans had up and
down place value!
But this
is 21
Thanks to: http://www.michielb.nl/maya/math.html
Could we count with lights?
How?
So….
• If this is one:
• And this is two:
• Then the sum is:
OOOOx
OOOxO
O O O xx
(1)
(10)
(11)
Lights, Lights, Lights!
Light 5 Light 4 Light 3 Light 2 Light 1
1. __
2. __
3. __
4. __
5. __
6. __
O
O
O
O
O
O
O
O
O
O
O
O
O
O
O
x
x
x
O
x
x
O
O
x
x
O
x
O
x
O
Binary Number
(1’s and 0’s)
____1_______
____10______
____11______
____100_____
____101_____
____110_____
What to remember:
 1 is “on”
 0 is “off”
What is the value of each 1?
Has a value of 1
1
What is the value of each 1?
Has a value of 2
10
One’s Place
What is the value of each 1?
Has a value of 4
100
One’s Place
Two’s Place
What is the value of each 1?
Has a value of 8
1000
Four’s Place
Two’s Place
One’s Place
So the value of this binary
number would be
8
1111
4
2
=8+4+2+1
1
= 15
So let’s double some numbers
 101
 11
 111
 100
 1010
 1010
 110
 1110
 1000
 10100
 Is there a pattern?
 Is it similar to a
pattern we use in
our system?
 Why does it work
for doubling?
So to double over and over…
• Add a zero each time you double
• So in our number system we would write
1 x 2 x 2 x 2 if we wanted to double the
number 1 three times.
• The shortcut for that would be 1 x 23
• In binary that number would be…
• 1000 (a zero for each double!)
Exponent
Try writing these answers in binary -3 is 11 so with four zeroes it would be…
3 x 24
3
4x2
5
7x2
13 x 23
= 110000
= 100 000
= 11100000
= 1101000
Guess what uses the binary
system?
So back to the Birthday Cards
• What is so special about
the numbers on card #1?
• Look at your lights,
lights, lights sheet and
tell me if the numbers
have something in
common in binary.
• What about card #2? #3?
#4? And #5?
Card #1
1
3
5
7
9
17
25
11
19
27
13
21
29
15
23
31
Birthday Cards
Card #2
Card #1
1
9
17
25
3
11
19
27
5
13
21
29
7
15
23
31
Card #4
Card #3
4
12
20
5
13
21
6
14
22
7
15
23
28
29
30
31
2
10
3
11
6
14
7
15
18
26
19
27
22
30
23
31
Card #5
8
12
9
13
10
14
11
15
16
20
17
21
18
22
19
23
24
28
25
29
26
30
27
31
24
28
25
29
26
30
27
31
So our base 10 system has shortcuts too…
• If binary had a shortcut for doubling ( x 2)
then our system has one for…
• x 10
• So if I want to multiply a number by ten all
I have to do is _______ ?
• And if I want to multiply by ten twice or
three times?
For Example
• 34 x 10 = 340
• 723 x 104 = 7,230,000
• 9 x 107 = 90,000,000
• 4,571 x 102 = 457,100
• 500 x 103 = 500,000
• This is TOO easy!
Let’s look at a different
number system --
Xmania
How do the Xmanians count?
Our Number System
Xmania
How is Xmania like our
decimal system?
• Has a digit for zero.
• Uses place value (except they add digits to
the left instead of the right).
• Has shortcuts for multiplying.
• _________________
• _________________
Now it’s your turn to
Your system should have:
•
•
•
•
•
A name
A digit for “zero”
3 or 4 digits total
Place value
Multiplication shortcut (with explanation)
Let’s sum up!
• How are place valued
number systems alike?
• What are the major
differences?
• What are the shortcuts to
our number system?
• Do the number shortcuts
work with other number
systems (like Xmania)?
Let’s sum up!
• Here’s a few for
you to review:
• 65 x 104 = 650,000
• 784 x 103 = 784,000
• 4 x 105 = 400,000
• 93 x 10 = 930
Questions?
Good-bye!