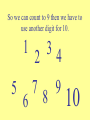* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Xmania! - MathinScience.info
Survey
Document related concepts
Transcript
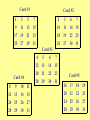
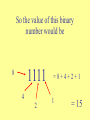
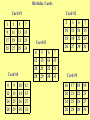
Count on it What day is your birthday? Think of the DATE you were born, but don’t say it out loud! Card #1 Card #2 1 9 17 3 11 19 5 13 21 7 15 23 2 10 18 3 11 19 6 7 14 15 22 23 25 27 29 31 26 27 30 31 Card #3 Card #4 4 5 6 7 12 20 28 13 21 29 14 22 30 15 23 31 Card #5 8 9 10 11 16 17 18 19 12 24 28 13 25 29 14 26 30 15 27 31 20 24 28 21 25 29 22 26 30 23 27 31 What to expect… • Learn some new things about our number system. • Learn some stuff about other number systems. • Learn some cool short-cuts that work for our number system. • Learn how the Birthday cards work. Let’s look at what we know: • How many digits are there? 10 digits • How many numbers are there? ∞ (infinity) • Do we have to use 1,2,3… or can we use something else? Any symbol will work. • Do we know any other number systems? Yes! • When is 8 + 5 = 1? On a Clock! So what is the value of -- 34 Why is it not 7? So we can count to 9 then we have to use another digit for 10. 1 34 2 5 7 8 9 6 10 Back in the day… • Different groups used different symbols. • Symbols could be a single value or different values (depending on where they were). • Here’s some examples: Here’s a few the Egyptians used So what’s their value? © Mark Millmore 1997 - 2004 A Few Mayan Math Symbols In Mayan Math This is 1 This is 2 The Mayans had up and down place value! But this is 21 Thanks to: http://www.michielb.nl/maya/math.html Could we count with lights? How? So…. • If this is one: • And this is two: • Then the sum is: OOOOx OOOxO O O O xx (1) (10) (11) Lights, Lights, Lights! Light 5 Light 4 Light 3 Light 2 Light 1 1. __ 2. __ 3. __ 4. __ 5. __ 6. __ O O O O O O O O O O O O O O O x x x O x x O O x x O x O x O Binary Number (1’s and 0’s) ____1_______ ____10______ ____11______ ____100_____ ____101_____ ____110_____ What to remember: 1 is “on” 0 is “off” What is the value of each 1? Has a value of 1 1 What is the value of each 1? Has a value of 2 10 One’s Place What is the value of each 1? Has a value of 4 100 One’s Place Two’s Place What is the value of each 1? Has a value of 8 1000 Four’s Place Two’s Place One’s Place So the value of this binary number would be 8 1111 4 2 =8+4+2+1 1 = 15 So let’s double some numbers 101 11 111 100 1010 1010 110 1110 1000 10100 Is there a pattern? Is it similar to a pattern we use in our system? Why does it work for doubling? So to double over and over… • Add a zero each time you double • So in our number system we would write 1 x 2 x 2 x 2 if we wanted to double the number 1 three times. • The shortcut for that would be 1 x 23 • In binary that number would be… • 1000 (a zero for each double!) Exponent Try writing these answers in binary -3 is 11 so with four zeroes it would be… 3 x 24 3 4x2 5 7x2 13 x 23 = 110000 = 100 000 = 11100000 = 1101000 Guess what uses the binary system? So back to the Birthday Cards • What is so special about the numbers on card #1? • Look at your lights, lights, lights sheet and tell me if the numbers have something in common in binary. • What about card #2? #3? #4? And #5? Card #1 1 3 5 7 9 17 25 11 19 27 13 21 29 15 23 31 Birthday Cards Card #2 Card #1 1 9 17 25 3 11 19 27 5 13 21 29 7 15 23 31 Card #4 Card #3 4 12 20 5 13 21 6 14 22 7 15 23 28 29 30 31 2 10 3 11 6 14 7 15 18 26 19 27 22 30 23 31 Card #5 8 12 9 13 10 14 11 15 16 20 17 21 18 22 19 23 24 28 25 29 26 30 27 31 24 28 25 29 26 30 27 31 So our base 10 system has shortcuts too… • If binary had a shortcut for doubling ( x 2) then our system has one for… • x 10 • So if I want to multiply a number by ten all I have to do is _______ ? • And if I want to multiply by ten twice or three times? For Example • 34 x 10 = 340 • 723 x 104 = 7,230,000 • 9 x 107 = 90,000,000 • 4,571 x 102 = 457,100 • 500 x 103 = 500,000 • This is TOO easy! Let’s look at a different number system -- Xmania How do the Xmanians count? Our Number System Xmania How is Xmania like our decimal system? • Has a digit for zero. • Uses place value (except they add digits to the left instead of the right). • Has shortcuts for multiplying. • _________________ • _________________ Now it’s your turn to Your system should have: • • • • • A name A digit for “zero” 3 or 4 digits total Place value Multiplication shortcut (with explanation) Let’s sum up! • How are place valued number systems alike? • What are the major differences? • What are the shortcuts to our number system? • Do the number shortcuts work with other number systems (like Xmania)? Let’s sum up! • Here’s a few for you to review: • 65 x 104 = 650,000 • 784 x 103 = 784,000 • 4 x 105 = 400,000 • 93 x 10 = 930 Questions? Good-bye!