Download (-2) + - Miami Beach Senior High School

Name:
Date:
Period:
EOC Practice:
1.
2.
Based on the diagram, what is the total number of
students who did not participate in soccer or
basketball?
INTEGERS???
Name:
Date:
Period:
Topic: To find sums, differences, products, and quotients of real numbers
Essential Question: How do the rules of integers relate to the properties of real numbers and the
definitions of operations?
Vocabulary:
Integers =
Whole Numbers =
Natural Numbers =
{…, -2, -1, 0, 1, 2, …}
{0, 1, 2, …}
{1, 2, 3, …}
ADDITION RULE
1) When the signs are the same,
ADD and keep the sign.
(-2) + (-4) = -6
2) When the signs are different,
SUBTRACT and use the sign of the
larger number.
(-2) + 4 = 2
2 + (-4) = -2
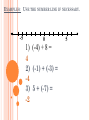
EXAMPLES: USE THE NUMBER LINE IF NECESSARY.
-5
0
1) (-4) + 8 =
4
2) (-1) + (-3) =
-4
3) 5 + (-7) =
-2
5
-1 + 3 = ?
1.
2.
3.
4.
-4
-2
2
4
Answer Now
-6 + (-3) = ?
1.
2.
3.
4.
-9
-3
3
9
Answer Now
WHEN SUBTRACTING, CHANGE THE SUBTRACTION TO
ADDING THE OPPOSITE (KEEP-CHANGE-CHANGE) AND THEN
FOLLOW YOUR ADDITION RULE.
Example #1:
- 4 - (-7)
- 4 + (+7)
Diff. Signs --> Subtract and use larger sign.
3
Example #2:
-3-7
- 3 + (-7)
Same Signs --> Add and keep the sign.
-10
Okay, here’s one with a variable!
Example #3: 11b - (-2b)
11b + (+2b)
Same Signs --> Add and
keep the sign.
13b
WHICH IS EQUIVALENT TO
-12 – (-3)?
1.
2.
3.
4.
12 + 3
-12 + 3
-12 - 3
12 - 3
Answer Now
7 – (-2) = ?
1.
2.
3.
4.
-9
-5
5
9
Answer Now
SIMPLIFY:
8
–7=
5 + (-3) =
15 + 2 =
-6 + 4 =
-9 – 3 =
-2 + (-1) =
-10 – (-12) =
17 – (-13) =
Review
1) IF THE PROBLEM IS ADDITION,
FOLLOW YOUR ADDITION RULE.
2) IF THE PROBLEM IS SUBTRACTION,
CHANGE SUBTRACTION TO ADDING THE
OPPOSITE
(KEEP-CHANGE-CHANGE) AND THEN
FOLLOW
THE ADDITION RULE.
SAME RULE APPLIES TO ABSOLUTE VALUE
Absolute Value
of a number is the distance from zero.
Distance can NEVER be negative!
The symbol is |a|, where a is any
number.
-5
0
5
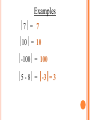
Examples
7 = 7
10 = 10
-100 = 100
5 - 8 = -3= 3
|7| – |-2| = ?
1.
2.
3.
4.
-9
-5
5
9
Answer Now
|-4 – (-3)| = ?
1.
2.
3.
4.
-1
1
7
Purple
Answer Now
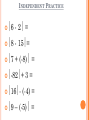
INDEPENDENT PRACTICE
6
- 2 =
8
- 15=
7
+ (-8) =
-82+
169
3=
(-4) =
– (-5) =
MULTIPLYING AND DIVIDING INTEGERS
If:
Then:
(+3) x (-7) = (-21)
(-21) ÷ (+3) = (-7)
(-5) x (-4) = (+20)
(+20) ÷ (-5) = (-4)
(-3) x (+8) = (-24)
(-24) ÷ (-3) = (+8)
(+5) x (+6) = (+30)
(+30) ÷ (+5) = (+6)
Are the rules the same?
Yes!
MULTIPLYING AND DIVIDING INTEGERS
RULES:
1) When multiplying or dividing integers with the same
signs, the answer will be positive.
2) When multiplying or dividing integers with different
signs, the answer will be negative.
Multiplying & Dividing Rule:
Positive times Positive =
Positive ( + · + = +)
Negative times Negative =
Positive ( - · - = +)
Positive times Negative =
Negative ( + · - = -)
Negative times Positive =
Negative ( - · + = -)
PRACTICE:
3 • -4 =
-7 • -2 =
8•3=
-9 • 2 =
30 ÷ -2 =
-24 ÷ -6 =
-4 ÷ 2 =
14 ÷ 7 =
1. A deep-sea diver must move up or down in
the water in short steps in order to avoid
getting a physical condition called the bends.
Suppose a diver moves up to the surface in five
steps of 11 feet. Represent her total
movements as a product of integers, and find
the product.
Multiply
(5 steps) (11 feet)
(55 feet)
5 · 11 = 55
2. At noon the temperature is 8°C. If
the temperature decreases 4°C per hour,
what is the temperature at 6 pm?
How long
Is it from
Noon
to 6 pm?
6
hours
-4
degrees
How much
does the
temperature
decrease
each
hour?
(6 hours)(- 4 degrees per hour)
= - 24 degrees
8° + (- 24°) = - 16°C
Add this to
the original temp.