Download Polynomial

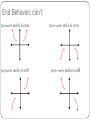
Polynomial Functions:
What is a polynomial function?
Module 2 Lesson 2
What is a Polynomial?
A polynomial is expression in the form:
f ( x)  an x  an 1 x
n
n 1
 ...  ax  c
where
 The coefficients (the a values) are real numbers
 The exponents (the n values) are whole numbers (positive
integers)
 The domain is All Real Numbers.
Examples
Polynomials
NOT Polynomials
y  5x  2 x  4
y  3x  4 x  1
3 6
f ( x)  x  7 x 3  x
4
5
f ( x)   3
x
3
3
Exponents
are not
positive
integers!
Ways to define polynomials
 By Degree
 The largest degree of the function is the degree of the polynomial
 By the number of terms.
 Count the number of terms in the expression.
State the degree of the following polynomial functions
3
8
5
12
Defining using number of terms
Monomial: A number, a variable or the product of a number and one
or more variables.
Binomial: A polynomial with exactly two terms.
Trinomial: A polynomial with exactly three terms.
Polynomial: A monomial or a sum of monomials.
For four or more terms, we just call it a polynomial.
Classify the polynomials by degree and
number of terms
Polynomial
Degree
5
Zero
Constant
Monomial
b.
2x  4
First
Linear
Binomial
c.
3x 2  x
Second
Quadratic
Binomial
Third
Cubic
Trinomial
Fourth
Quartic
a.
.
d.
x3  4 x 2  1
e. 3x4 - 4x3 + 6x2 - 7
f. 8x7 - 7x - 9
Seventh
Classify by degree
Septic or Heptic
Classify by number of terms
Polynomial
Trinomial
Solving Polynomial Equations
To solve a polynomial equation you will find the x – intercepts.You find x-intercepts by
letting y = 0 and then using the Zero Product Property (just like when you were
solving quadratics!). Intercepts can be referred to as solutions, roots, or zeros.
The maximum number of solutions a polynomial can
have is limited by the degree of the polynomial!
If f(r) = 0 and r is a real number, then r is a real zero of the function and….
… r is an x-intercept of the graph of the function.
… (x – r) is a factor of the function.
… r is a solution to the function f(x) = 0
Multiplicities
Sometimes a solution will appear more than once. This solution has a
multiplicity.
To find a Multiplicity
Count the number of times a factor (m) of a function is repeated.
Multiplicities appearing an Even Number of times
The graph of the function touches the x-axis but does not cross it.
Multiplicities appearing an Odd Number of times
The graph of the function crosses the x-axis.
Identify the zeros and their multiplicity
3 is a zero with a multiplicity of 1. Graph crosses the x-axis at x = 3
-2 is a zero with a multiplicity of 3. Graph crosses the x-axis at x = -2.
-4 is a zero with a multiplicity of 1.
Graph crosses the x-axis at x = -4.
7 is a zero with a multiplicity of 2.
Graph touches the x-axis at x = 7.
-1 is a zero with a multiplicity of 1.
Graph crosses the x-axis at x = -1.
4 is a zero with a multiplicity of 1.
Graph crosses the x-axis at x = 4
2 is a zero with a multiplicity of 2.
Graph touches the x-axis at x = 2
End Behavior of a Polynomial
You can predict what directions the ends of the graph
are going based on the sign of the leading coefficient
and the degree of the polynomial.
End Behavior, con’t
Time to put it all together!
For the following polynomial:
 Define by number of terms and degree,
 State number of possible solutions,
 Find zeros and state multiplicities,
 Describe multiplicities,
 Describe the end behavior, and
 Sketch graph.
f ( x)  ( x  1)( x  2)
2
f ( x)  ( x  1)( x  2)
2
 Define by number of terms and degree and state number of possible
solutions
To find the degree and the number of terms, we will need to distribute.
f ( x)  ( x  1)( x  2)( x  2)
 ( x  1)( x 2  4 x  4)
 x3  4 x 2  4 x  x 2  4 x  4
 x 3  3x 2  4
So we have a third degree, or cubic, trinomial. This
trinomial will have a maximum of 3 unique solutions.
f ( x)  ( x  1)( x  2)
2
• Find zeros and state multiplicities and describe multiplicities.
0  ( x  1)( x  2)
0  x 1
0 x2
x 1
x  2
2
The solutions to this polynomial are x = 1 and x = -2.
The zero at x =1 has a multiplicity of 1. The graph will cross the x-axis at 1.
The zero at x = -2 has a multiplicity of 2 and will touch the x-axis.
f ( x)  ( x  1)( x  2) 2  x 3  3 x 2  4
 Describe the end behavior and Sketch graph.
Since n = 3, an odd number, we know that the end behavior
will be split- one side will be going up and the other side will
be going down.
As a = +1, the graph will being going up from left to right. So
the left side of the graph is pointing down and the right side of
the graph is pointing up.
Sketch the Graph
1.
Plot zeros
2.
Choose a point in
between zeros to help
find turning point.
Let x = -1
y = (-2)(-1+2)2 = -2
3.
Find y-intercept
Let x = 0
y = (-1)(2)2 = -4
4.
Plot the other points.
5.
Use end behavior and
intercepts to graph.