Download 4.2 - People Server at UNCW

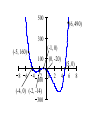
4.2
Polynomial Functions and
Models
A polynomial function is a function of the form
Determine which of the following are
polynomials. For those that are, state the
degree.
2
(a) f ( x ) = 3x - 4 x + 5 Polynomial.
(b)
(c)
Not a polynomial.
Not a polynomial.
If f is a polynomial function and r is a real number
for which f(r)=0, then r is called a (real) zero of
f, or root of f. If r is a (real) zero of f, then
(a) r is an x-intercept of the graph of f.
(b) (x-r) is a factor of f.
Use the above to conclude that x = -1 and x = 4 are
the real roots (zeroes) of f.
1 is a zero of multiplicity 2.
-3 is a zero of multiplicity 1.
-5 is a zero of multiplicity 5.
If r is a Zero or Even Multiplicity
If r is a Zero or Odd Multiplicity
.
Theorem
If f is a polynomial function of degree
n, then f has at most n-1 turning points.
Theorem
For large values of x, either positive
or negative, the graph of the
polynomial
resembles the graph of the power function.
For the polynomial
(a) Find the x- and y-intercepts of the graph of f.
(b) Determine whether the graph crosses or
touches the x-axis at each x-intercept.
(c) Find the power function that the graph of f
resembles for large values of x.
(d) Determine the maximum number of turning
points on the graph of f.
For the polynomial
(e) Use the x-intercepts and test numbers to find
the intervals on which the graph of f is above the
x-axis and the intervals on which the graph is
below the x-axis.
(f) Put all the information together, and connect
the points with a smooth, continuous curve to
obtain the graph of f.
(a) The x-intercepts are -4, -1, and 5.
y-intercept:
(b) -4 is a zero of multiplicity 1. (crosses)
-1 is a zero of multiplicity 2. (touches)
5 is a zero of multiplicity 1. (crosses)
(d) At most 3 turning points.
Test number:
f (-5)
Graph of f:
-5
160
Above x-axis
Point on graph: (-5, 160)
-4 < x <-1
Test number:
-2
f (-2)
-14
Graph of f:
Below x-axis
Point on graph: (-2, -14)
-1 < x < 5
Test number:
f (0)
Graph of f:
0
-20
Below x-axis
Point on graph: (0, -20)
Test number:
f (6)
Graph of f:
6
490
Above x-axis
Point on graph: (6, 490)
500
(6, 490)
300
(-1, 0)
100 (0, -20)
(-5, 160)
8
6
4
2
100
(-4, 0) (-2, -14)
300
0
2
(5, 0)
4
6
8