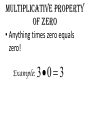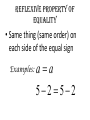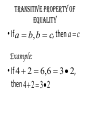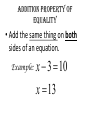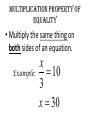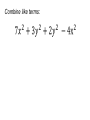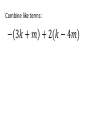* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 1-1 Patterns and Expressions
Linear algebra wikipedia , lookup
Field (mathematics) wikipedia , lookup
System of linear equations wikipedia , lookup
System of polynomial equations wikipedia , lookup
Signal-flow graph wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Exterior algebra wikipedia , lookup
Clifford algebra wikipedia , lookup
Algebraic variety wikipedia , lookup
Elementary algebra wikipedia , lookup
Homomorphism wikipedia , lookup
Canonical normal form wikipedia , lookup
1-1 Patterns and Expressions Algebra 2 1 Identifying Patterns Patterns can be represented using words, diagrams, numbers, or algebraic expressions. What is the next figure? Algebra 2 2 Look at the figures from right to left. What is the pattern? Algebra 2 3 Try this on your own. Draw the next figure. Algebra 2 4 Numerical Pattern What is the next number in the pattern 2, 4, 6, 8, …. 6, 3, 0, -3, …. Algebra 2 5 Variable- a symbol, usually a letter that represents one or more numbers ex: x or n Numerical Expression- mathematical phrase that contains numbers and operation symbols. ex: 3+5 Algebraic Expressions- mathematical phrase that contains one or more variables ex: 3n+5 Algebra 2 6 Using Tables to help identify patterns Input Process Column Output 1 0 2 1 3 2 4 3 5 n Algebra 2 7 Input Process Column Output 1 5 2 9 3 13 4 17 5 n Algebra 2 8 Expressing a Pattern with Algebra How many toothpicks are in the 20th figure? Figure Number (Input) Process Column Number of Toothpicks (output) 1 1(4) 4 2 2(4) 8 3 3(4) 12 n Algebra 2 9 Patterns on Graphs The graph shows the cost depending on the number of DVDs that you purchase. What is the cost of purchasing 5 DVD’s? 10 DVD’s? Input (x value) Process Column Output (y-value) 0 0 1 16 2 32 Algebra 2 10 Section 1-1 Overview • Patterns- look at the figures or numbers from left to right and identify the pattern. • Variables are used in math to represent an unknown number in equations and inequalities. • Using Input/Output tables can help you find patterns. Algebra 2 11 Warm Up Section 1-2 Properties of Real Numbers Commutative property • Order doesn’t matter! Examples: 4 3 3 4 Of Multiplication:4 3 3 4 Of Addition: associative property • Order stays the same, but the terms are regrouped. Examples: 1 2 3 1 2 3 Of Addition: Of Multiplication:1 2 3 1 2 3 Additive identity • Add zero to a term so the term does not change Example: 3 0 3 multiplicative identity • Multiply by one so the term does not change Example: 3 1 3 Multiplicative property of zero • Anything times zero equals zero! Example: 3 0 3 Distributive property • Multiply to each term inside parenthesis Examples: 4x 2 4x 8 x 24 4x 8 Substitution property of equality • Replacing an expression by another expression of the same value Example: 4 10 8 14 8 Symmetric property of equality • Switch sides! (do not change order of terms on each side) Examples: If If 3 7 10, then 10 3 7 7x then x7 Reflexive property of equality • Same thing (same order) on each side of the equal sign Examples: aa 52 52 Transitive property of equality • If a b, b c, then a c Example: • If 4 2 6,6 3 2, then 4 2 3 2 Addition property of equality • Add the same thing on both sides of an equation. Example: x 3 10 x 13 Subtraction property of equality • Subtract the same thing on both sides of an equation. Example: x 3 10 x7 multiplication property of equality • Multiply the same thing on both sides of an equation. Example: x 10 3 x 30 division property of equality • Divide the same thing on both sides of an equation. Example: 3x 12 x4 1-3 Algebraic Expressions Modeling Words with an Algebraic Expression Seven fewer than t t+7 -7t t-7 7-t Think: What operation does ‘seven fewer than t’ suggest? Key Words to Identify Operations Addition (+) Subtraction (-) Multiplication (x) Division (÷) Sum Difference Product Quotient More than Less than Times Divided by Increased by Fewer than of Total Subtracted by Added to minus Practice 1. The difference of a number p and 36 2. 15 more than the number q 3. The product of 10 and a number r 4. The total of a number y and 9 Modeling a Situation To model a situation with an algebraic expression do the following: •Identify the actions that suggest operations •Define one or more variables to represent the unknown (s). •Represent the actions using the variables and the operations. You start with $20 and save $6 each week. What algebraic expression models the total amount you save? Determine which quantity is unknown. Starting amount plus Amount saved times 6 x Number of weeks Let w = the number of weeks 20 + w Evaluating Algebraic Expressions • To evaluate an algebraic expression, substitute a number for each variable in the expression. Then simplify using the order of operations. What is the value of the expression for the given values of the variables. for a = -4 and b = 5 Evaluate: For x=6 and y=-3 Important Vocab • Term- a number, a variable, or the product of a number and one or more variables. • Coefficient- the numerical factor of a term. • Constant term- a term with no variables -4ax + 7w - 6 coefficient term Constant term Combine like terms: Combine like terms: