algebra boolean circuit outline schaums switching
... clear statements of pertinent definitions, principles and theorems together with illustrative and other descriptive material. This is followed by graded sets of solved and supplementary problems. The solved problems serve to illustrate and amplify the theory, bring into sharp focus those fine points ...
... clear statements of pertinent definitions, principles and theorems together with illustrative and other descriptive material. This is followed by graded sets of solved and supplementary problems. The solved problems serve to illustrate and amplify the theory, bring into sharp focus those fine points ...
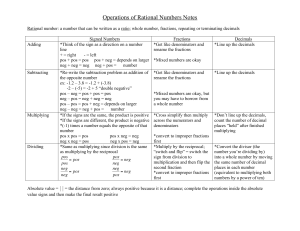
Operations of Rational Numbers Notes
... *Multiply by the reciprocal; “switch and flip” = switch the sign from division to multiplication and then flip the second fraction *convert to improper fractions first ...
... *Multiply by the reciprocal; “switch and flip” = switch the sign from division to multiplication and then flip the second fraction *convert to improper fractions first ...
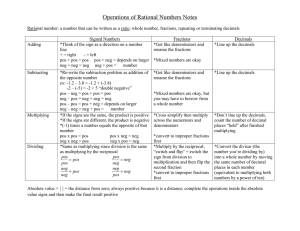
Operations of Rational Numbers Notes
... *Multiply by the reciprocal; “switch and flip” = switch the sign from division to multiplication and then flip the second fraction *convert to improper fractions first ...
... *Multiply by the reciprocal; “switch and flip” = switch the sign from division to multiplication and then flip the second fraction *convert to improper fractions first ...
Min terms and logic expression
... • Simplify Boolean expression for carry function in a 3-bit adder • Cout = a’.b.cin + a.b’.cin + a.b.cin’ + a.b.cin – Each of the first, second, and third term can be combined with the last term – Use identity to make copies of the last term 3 times (x+x=x) – Cout = a’.b.cin + a.b’.cin + a.b.cin’ + ...
... • Simplify Boolean expression for carry function in a 3-bit adder • Cout = a’.b.cin + a.b’.cin + a.b.cin’ + a.b.cin – Each of the first, second, and third term can be combined with the last term – Use identity to make copies of the last term 3 times (x+x=x) – Cout = a’.b.cin + a.b’.cin + a.b.cin’ + ...
Functions as Passive Constraints in LIFE
... The first extension is based on -terms which are attributed partially-ordered sorts denoting sets of objects [1, 3]. In particular, -terms generalize first-order constructor terms in their rôle as data structures in that they are endowed with a unification operation denoting type intersection. This ...
... The first extension is based on -terms which are attributed partially-ordered sorts denoting sets of objects [1, 3]. In particular, -terms generalize first-order constructor terms in their rôle as data structures in that they are endowed with a unification operation denoting type intersection. This ...
The Building Blocks: Binary Numbers, Boolean Logic, and Gates
... • Electronic devices work best in a bistable environment, that is, where there are only 2 states. • Can build a computer using a binary storage device: – Has two different stable states, able to sense in which state device is in, and easily switch between states. ...
... • Electronic devices work best in a bistable environment, that is, where there are only 2 states. • Can build a computer using a binary storage device: – Has two different stable states, able to sense in which state device is in, and easily switch between states. ...
EE 457 Unit 4a Signed Systems Unsigned and Signed Variables
... • Convert the MS-hex digit to binary to determine the MSB (e.g. for B2 hex, B=1011 so since the MSB=1, B2 is neg.) ...
... • Convert the MS-hex digit to binary to determine the MSB (e.g. for B2 hex, B=1011 so since the MSB=1, B2 is neg.) ...
3. Abstract Boolean Algebras 3.1. Abstract Boolean Algebra.
... As these examples illustrate, the names for addition and multiplication in a particular Boolean algebra may be idiomatic to that example. Addition may be called sum, union, join, or disjunction; whereas, multiplication may be called product, intersection, meet, or conjunction. Because the addition a ...
... As these examples illustrate, the names for addition and multiplication in a particular Boolean algebra may be idiomatic to that example. Addition may be called sum, union, join, or disjunction; whereas, multiplication may be called product, intersection, meet, or conjunction. Because the addition a ...
Number Systems and Conversion + Boolean Algebra
... components, such as resistors and transistors, to form a gate, flip-flop, or other logic block ...
... components, such as resistors and transistors, to form a gate, flip-flop, or other logic block ...
Chapter 13 BOOLEAN ALGEBRA
... Notice that the two definitions above refer to "...a greatest lower bound" and "a least upper bound." Any time you define an object like these you need to have an open mind as to whether more than one such object can exist. In fact, we now can prove that there can't be two greatest lower bounds or t ...
... Notice that the two definitions above refer to "...a greatest lower bound" and "a least upper bound." Any time you define an object like these you need to have an open mind as to whether more than one such object can exist. In fact, we now can prove that there can't be two greatest lower bounds or t ...
PDF
... f (a1 , . . . , an ), where each aj ∈ Xi . So aj ∈ hXi by hypothesis. Since hXi is inductive, f (a1 , . . . , an ) ∈ hXi, and hence a ∈ hXi as well. This shows that Xi+1 ⊆ A, and consequently X ⊆ hXi. The inductive set A is said to be freely generated by X (with respect to F ), if the following con ...
... f (a1 , . . . , an ), where each aj ∈ Xi . So aj ∈ hXi by hypothesis. Since hXi is inductive, f (a1 , . . . , an ) ∈ hXi, and hence a ∈ hXi as well. This shows that Xi+1 ⊆ A, and consequently X ⊆ hXi. The inductive set A is said to be freely generated by X (with respect to F ), if the following con ...
Evaluate Expressions
... multiplication of the same factor Base The number or expression that is used as a factor in repeated multiplication Exponent A number or expression that represents the number of times the base is used as a factor ...
... multiplication of the same factor Base The number or expression that is used as a factor in repeated multiplication Exponent A number or expression that represents the number of times the base is used as a factor ...
Multiplying Out and Factoring
... • Binary decision diagrams, which will be used later to build arbitrary circuits with 2-input muxes. Why we say Σ of Π for Sum of Product ...
... • Binary decision diagrams, which will be used later to build arbitrary circuits with 2-input muxes. Why we say Σ of Π for Sum of Product ...
TERNARY BOOLEAN ALGEBRA 1. Introduction. The
... operation in Boolean algebra. We assume a degree of familiarity with the latter [l, 2 ] , 2 and by the former we shall mean simply a function of three variables defined for elements of a set K whose values are also in K. Ternary operations have been discussed in groupoids [4] and groups [3 ] ; in Bo ...
... operation in Boolean algebra. We assume a degree of familiarity with the latter [l, 2 ] , 2 and by the former we shall mean simply a function of three variables defined for elements of a set K whose values are also in K. Ternary operations have been discussed in groupoids [4] and groups [3 ] ; in Bo ...
Solve Inequ w var on both sides
... Variables on Both Sides Some inequalities have variable terms on both sides of the inequality symbol. You can solve these inequalities like you solved equations with variables on both sides. Use the properties of inequality to “collect” all the variable terms on one side and all the constant terms o ...
... Variables on Both Sides Some inequalities have variable terms on both sides of the inequality symbol. You can solve these inequalities like you solved equations with variables on both sides. Use the properties of inequality to “collect” all the variable terms on one side and all the constant terms o ...
FunctionalDependencies2
... Let R be a relation schema that is decomposed into two schemas with attribute sets X and Y, and let F be a set of FD’s over R. The projection of F on X (denoted by FX) is the set of FD’s in F+ that involve only attributes in X Recall that a FD U V in F+ is in FX if all the attributes in U and V ...
... Let R be a relation schema that is decomposed into two schemas with attribute sets X and Y, and let F be a set of FD’s over R. The projection of F on X (denoted by FX) is the set of FD’s in F+ that involve only attributes in X Recall that a FD U V in F+ is in FX if all the attributes in U and V ...
Fibonacci Numbers - Lehigh University
... by a constant in the expressions we gave previously. Using tools from linear algebra it can be shown that if the corresponding polynomial has degree d and its roots are distinct then d initial conditions will suffice to give a formula in a manner analogous to that described above. When there are rep ...
... by a constant in the expressions we gave previously. Using tools from linear algebra it can be shown that if the corresponding polynomial has degree d and its roots are distinct then d initial conditions will suffice to give a formula in a manner analogous to that described above. When there are rep ...