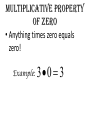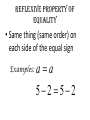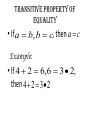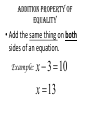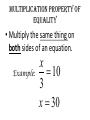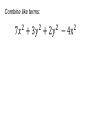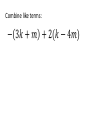Download 1-1 Patterns and Expressions

1-1 Patterns and Expressions
Algebra 2
1
Identifying Patterns
Patterns can be represented using words,
diagrams, numbers, or algebraic expressions.
What is the next figure?
Algebra 2
2
Look at the figures from right to left.
What is the pattern?
Algebra 2
3
Try this on your own.
Draw the next figure.
Algebra 2
4
Numerical Pattern
What is the next number in the pattern
2, 4, 6, 8, ….
6, 3, 0, -3, ….
Algebra 2
5
Variable- a symbol, usually a letter that
represents one or more numbers
ex:
x
or
n
Numerical Expression- mathematical phrase that
contains numbers and operation symbols.
ex: 3+5
Algebraic Expressions- mathematical phrase that
contains one or more variables
ex: 3n+5
Algebra 2
6
Using Tables to help identify patterns
Input
Process Column
Output
1
0
2
1
3
2
4
3
5
n
Algebra 2
7
Input
Process Column
Output
1
5
2
9
3
13
4
17
5
n
Algebra 2
8
Expressing a Pattern with Algebra
How many toothpicks are in the 20th figure?
Figure
Number
(Input)
Process Column
Number of
Toothpicks
(output)
1
1(4)
4
2
2(4)
8
3
3(4)
12
n
Algebra 2
9
Patterns on Graphs
The graph shows the cost depending on the number of DVDs that you purchase.
What is the cost of purchasing 5
DVD’s?
10 DVD’s?
Input
(x value)
Process Column
Output
(y-value)
0
0
1
16
2
32
Algebra 2
10
Section 1-1 Overview
• Patterns- look at the figures or numbers from
left to right and identify the pattern.
• Variables are used in math to represent an
unknown number in equations and
inequalities.
• Using Input/Output tables can help you find
patterns.
Algebra 2
11
Warm Up
Section 1-2
Properties of
Real Numbers
Commutative property
• Order doesn’t matter!
Examples:
4 3  3 4
Of Multiplication:4  3  3  4
Of Addition:
associative property
• Order stays the same, but the
terms are regrouped.
Examples:
1  2  3  1  2  3
Of
Addition:
Of Multiplication:1 2  3  1 2  3

 

Additive identity
• Add zero to a term so the term
does not change
Example:
3 0  3
multiplicative identity
• Multiply by one so the term
does not change
Example:
3 1  3
Multiplicative property
of zero
• Anything times zero equals
zero!
Example:
3 0  3
Distributive property
• Multiply to each term inside
parenthesis
Examples:
4x  2  4x  8
x  24  4x  8
Substitution property
of equality
• Replacing an expression by
another expression of the
same value
Example:
4 10  8  14  8
Symmetric property of
equality
• Switch sides! (do not change
order of terms on each side)
Examples:
If
If
3  7  10, then 10  3  7
7x
then
x7
Reflexive property of
equality
• Same thing (same order) on
each side of the equal sign
Examples:
aa
52  52
Transitive property of
equality
• If a  b, b  c, then a  c
Example:
• If 4  2  6,6  3  2,
then 4  2  3  2
Addition property of
equality
• Add the same thing on both
sides of an equation.
Example:
x  3  10
x  13
Subtraction property of
equality
• Subtract the same thing on
both sides of an equation.
Example:
x  3  10
x7
multiplication property of
equality
• Multiply the same thing on
both sides of an equation.
Example:
x
 10
3
x  30
division property of equality
• Divide the same thing on both
sides of an equation.
Example:
3x  12
x4
1-3 Algebraic Expressions
Modeling Words with an Algebraic
Expression
Seven fewer than t
t+7
-7t
t-7
7-t
Think: What operation does ‘seven fewer than t’
suggest?
Key Words to Identify Operations
Addition (+)
Subtraction (-)
Multiplication (x) Division (÷)
Sum
Difference
Product
Quotient
More than
Less than
Times
Divided by
Increased by
Fewer than
of
Total
Subtracted by
Added to
minus
Practice
1. The difference of a number p and 36
2. 15 more than the number q
3. The product of 10 and a number r
4. The total of a number y and 9
Modeling a Situation
To model a situation with an algebraic
expression do the following:
•Identify the actions that suggest operations
•Define one or more variables to represent the
unknown (s).
•Represent the actions using the variables and
the operations.
You start with $20 and save $6 each week. What
algebraic expression models the total amount you
save?
Determine which quantity is unknown.
Starting
amount
plus
Amount
saved
times
6
x
Number of
weeks
Let w = the number of weeks
20
+
w
Evaluating Algebraic Expressions
• To evaluate an algebraic expression, substitute a number for
each variable in the expression. Then simplify using the order
of operations.
What is the value of the expression for the
given values of the variables.
for a = -4 and b =
5
Evaluate:
For x=6 and y=-3
Important Vocab
• Term- a number, a variable, or the product of
a number and one or more variables.
• Coefficient- the numerical factor of a
term.
• Constant term- a term with no variables
-4ax + 7w - 6
coefficient
term
Constant
term
Combine like terms:
Combine like terms: