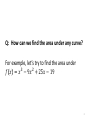* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Math 71 – 1.1
John Wallis wikipedia , lookup
Function of several real variables wikipedia , lookup
Infinitesimal wikipedia , lookup
Series (mathematics) wikipedia , lookup
Path integral formulation wikipedia , lookup
Divergent series wikipedia , lookup
Itô calculus wikipedia , lookup
Riemann integral wikipedia , lookup
Multiple integral wikipedia , lookup
Lebesgue integration wikipedia , lookup
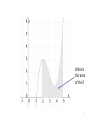
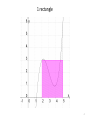
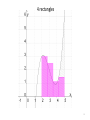
Math 140 5.3 – The Definite Integral and the Fundamental Theorem of Calculus 1 Q: How can we find the area under any curve? For example, let’s try to find the area under 𝑓 𝑥 = 𝑥 3 − 9𝑥 2 + 25𝑥 − 19 2 What is the area of this? 3 1 rectangle 4 2 rectangles 5 4 rectangles 6 50 rectangles 7 If the left sides of our rectangles are at 𝑥1 , 𝑥2 , …, 𝑥𝑛 and each rectangle has width Δ𝑥, then the areas of the rectangles are 𝑓 𝑥1 Δ𝑥, 𝑓 𝑥2 Δ𝑥, …, 𝑓 𝑥𝑛 Δ𝑥. So, the sum of the areas of the rectangles (called a Riemann sum) is: 𝑓 𝑥1 Δ𝑥 + 𝑓 𝑥2 Δ𝑥 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 = 𝑓 𝑥1 + 𝑓 𝑥2 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 8 So, the sum of the areas of the rectangles (called a Riemann sum) is: 𝑓 𝑥1 Δ𝑥 + 𝑓 𝑥2 Δ𝑥 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 = 𝑓 𝑥1 + 𝑓 𝑥2 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 9 So, the sum of the areas of the rectangles (called a Riemann sum) is: 𝑓 𝑥1 Δ𝑥 + 𝑓 𝑥2 Δ𝑥 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 = 𝑓 𝑥1 + 𝑓 𝑥2 + ⋯ + 𝑓 𝑥𝑛 Δ𝑥 10 As the number of rectangles (𝑛) increases, the above sum gets closer to the true area. That is, Area under curve = 𝒍𝒊𝒎 𝒇 𝒙𝟏 + 𝒇 𝒙𝟐 + ⋯ + 𝒇 𝒙𝒏 𝐧→+∞ 𝜟𝒙 11 𝑏 𝑓 𝑥 𝑑𝑥 = lim 𝑓 𝑥1 + 𝑓 𝑥2 + ⋯ + 𝑓 𝑥𝑛 𝑎 n→+∞ Δ𝑥 The above integral is called a definite integral, and 𝑎 and 𝑏 are called the lower and upper limits of integration. 12 The Fundamental Theorem of Calculus If 𝑓(𝑥) is continuous on the interval 𝑎 ≤ 𝑥 ≤ 𝑏, then 𝒃 𝒇 𝒙 𝒅𝒙 = 𝑭 𝒃 − 𝑭(𝒂) 𝒂 where 𝐹(𝑥) is any antiderivative of 𝑓(𝑥) on 𝑎 ≤ 𝑥 ≤ 𝑏. 13 Ex 1. Evaluate the given definite integrals using the fundamental theorem of calculus. 1 2𝑥 2 𝑑𝑥 −1 14 Ex 1. Evaluate the given definite integrals using the fundamental theorem of calculus. 1 2𝑥 2 𝑑𝑥 −1 15 Ex 1 (cont). Evaluate the given definite integrals using the fundamental theorem of calculus. 1 (𝑒 2𝑥 − 𝑥) 𝑑𝑥 0 16 Ex 1 (cont). Evaluate the given definite integrals using the fundamental theorem of calculus. 1 (𝑒 2𝑥 − 𝑥) 𝑑𝑥 0 17 Note: Definite integrals can evaluate to negative numbers. For example, 2 1 (1 − 𝑥) 𝑑𝑥 = − 1 2 18 Just like with indefinite integrals, terms can be integrated separately, and constants can be pulled out. 𝑏 𝑏 𝑓 𝑥 ± 𝑔(𝑥) 𝑑𝑥 = 𝑎 𝑏 𝑏 𝑘𝑓 𝑥 𝑑𝑥 = 𝑘 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 ± 𝑎 𝑔(𝑥) 𝑑𝑥 𝑎 𝑓 𝑥 𝑑𝑥 𝑎 Also, 𝑎 𝑓 𝑥 𝑑𝑥 = 0 𝑎 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 = − 𝑏 𝑓 𝑥 𝑑𝑥 𝑎 19 𝑏 𝑐 𝑓 𝑥 𝑑𝑥 = 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 + 𝑎 𝑓 𝑥 𝑑𝑥 𝑐 (here, 𝑐 is any real number) 20 𝑏 𝑐 𝑓 𝑥 𝑑𝑥 = 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 + 𝑎 𝑓 𝑥 𝑑𝑥 𝑐 (here, 𝑐 is any real number) = 21 𝑏 𝑐 𝑓 𝑥 𝑑𝑥 = 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 + 𝑎 𝑓 𝑥 𝑑𝑥 𝑐 (here, 𝑐 is any real number) = + 22 Ex 2. Let 𝑓(𝑥) and 𝑔(𝑥) be functions that are continuous on the interval − 3 ≤ 𝑥 ≤ 5 and that satisfy 5 5 𝑓 𝑥 𝑑𝑥 = 2 5 𝑔 𝑥 𝑑𝑥 = 7 −3 −3 𝑓 𝑥 𝑑𝑥 = −8 1 Use this information along with the rules definite integrals to evaluate the following. 5 2𝑓 𝑥 − 3𝑔 𝑥 𝑑𝑥 −3 1 𝑓 𝑥 𝑑𝑥 −3 23 Ex 3. Evaluate: 1 8𝑥 𝑥 2 + 1 3 𝑑𝑥 0 24 Ex 3. Evaluate: 1 8𝑥 𝑥 2 + 1 3 𝑑𝑥 0 25 Net Change If we have 𝑄′(𝑥), then we can calculate the net change in 𝑄(𝑥) as 𝑥 goes from 𝑎 to 𝑏 with an integral: 𝑏 𝑄 ′ 𝑥 𝑑𝑥 𝑄 𝑏 −𝑄 𝑎 = 𝑎 26 Net Change Ex 4. Suppose marginal cost is 𝐶 ′ 𝑥 = 3 𝑥 − 4 2 dollars per unit when the level of production is 𝑥 units. By how much will the total manufacturing cost increase if the level of production is raised from 6 units to 10 units? 27