PDF (Chapter 7)
... If n = - 2, - 3, - 4, . . . , a and b must have the same sign. If n is not an integer, a and b must be positive (or zero if > 0). ...
... If n = - 2, - 3, - 4, . . . , a and b must have the same sign. If n is not an integer, a and b must be positive (or zero if > 0). ...
... Transform, but has not been obtained until now. We establish it here for any hyper-real function in Infinitesimal Calculus, from the properties of the Delta Function. Nor were Conditions for the Existence of the Hilbert Transform established. In general, it may seem that the existence of the ...
MATH_125_online_L5__..
... doesn't matter. And we get that the difference between the antiderivative at a and b is the same regardless which antiderivative use. So in particular, since we already showed that this difference is equal to the definite integral, then G of b minus G of a is indeed equal to integral from a to b of ...
... doesn't matter. And we get that the difference between the antiderivative at a and b is the same regardless which antiderivative use. So in particular, since we already showed that this difference is equal to the definite integral, then G of b minus G of a is indeed equal to integral from a to b of ...
REVIEW FOR FINAL EXAM April 08, 2014 • Final Exam Review Session:
... n=1 approach a unique number L as n increase, that is, if an can be made arbitrarily close to L by taking n sufficiently large, then we say that the sequence {an } converges to L, denoted by lim an = L. If the terms of the sequence do not approach a single number as n increases, n→∞ ...
... n=1 approach a unique number L as n increase, that is, if an can be made arbitrarily close to L by taking n sufficiently large, then we say that the sequence {an } converges to L, denoted by lim an = L. If the terms of the sequence do not approach a single number as n increases, n→∞ ...
Integral Calculus - Exercises
... Therefore, the desired function is f (x) = 14 x4 + x2 + 2x − 54 . 9. It is estimated that t years from now the population of a certain lakeside community will be changing at the rate of 0.6t2 + 0.2t + 0.5 thousand people per year. Environmentalists have found that the level of pollution in the lake ...
... Therefore, the desired function is f (x) = 14 x4 + x2 + 2x − 54 . 9. It is estimated that t years from now the population of a certain lakeside community will be changing at the rate of 0.6t2 + 0.2t + 0.5 thousand people per year. Environmentalists have found that the level of pollution in the lake ...
Math 107H Topics for the first exam Integration Antiderivatives
... | a f (x) dx − M (f, n)| ≤ K (b−a) 24n2 In the end though, a midpoint estimate is throwing out a lot of information, since it approximates f on an interval by a constant. We can do better, taking into account more infmation about the function f , by approximating f by functions that better “fit” f o ...
... | a f (x) dx − M (f, n)| ≤ K (b−a) 24n2 In the end though, a midpoint estimate is throwing out a lot of information, since it approximates f on an interval by a constant. We can do better, taking into account more infmation about the function f , by approximating f by functions that better “fit” f o ...
Stochastic Calculus Notes, Lecture 7 1 The Ito integral with respect
... m=1 E [|Sm |] < ∞ and (using Borel Cantelli) that Sm → 0 as m → ∞ (almost surely). This argument would not have worked this√way had we taken n = m instead of n = 2m . The error bounds of order 1/ n would not have had a finite sum. If both error terms in the bottom line of (16) go to zero as m → ∞ wi ...
... m=1 E [|Sm |] < ∞ and (using Borel Cantelli) that Sm → 0 as m → ∞ (almost surely). This argument would not have worked this√way had we taken n = m instead of n = 2m . The error bounds of order 1/ n would not have had a finite sum. If both error terms in the bottom line of (16) go to zero as m → ∞ wi ...
Indefinite Integrals Calculus
... Use Riemann Sums with four subintervals of equal lengths. Choose the midpoints of each subinterval as the sample points. 2. Repeat problem #1 using geometry to calculate the exact area of the region under the graph of from to (Hint: Sketch a graph of the region and see if you can compute its area us ...
... Use Riemann Sums with four subintervals of equal lengths. Choose the midpoints of each subinterval as the sample points. 2. Repeat problem #1 using geometry to calculate the exact area of the region under the graph of from to (Hint: Sketch a graph of the region and see if you can compute its area us ...
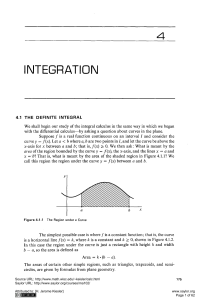
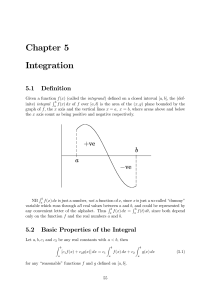
Chapter 5 Integration
... This is not a true proof since the “good approximation” is imprecise. A rigorous proof using precise definitions of continuity and of the Riemann integral will be given in MATH 2011 Real Analysis 2. The fundamental theorem provides a precise statement of the sense in which integration is the reverse ...
... This is not a true proof since the “good approximation” is imprecise. A rigorous proof using precise definitions of continuity and of the Riemann integral will be given in MATH 2011 Real Analysis 2. The fundamental theorem provides a precise statement of the sense in which integration is the reverse ...
CW 6 Solutions File
... k. dS = k.dS = (∇ · k) dV = 0 where we have taken the k inside the integral, then used the divergence theorem. The same holds for the i and j components, so the original (vector) expression is zero. (c) Again consider the k component: I I Z k · r × dS = (k × r) · dS = ∇ · (k × r) dV , using the prop ...
... k. dS = k.dS = (∇ · k) dV = 0 where we have taken the k inside the integral, then used the divergence theorem. The same holds for the i and j components, so the original (vector) expression is zero. (c) Again consider the k component: I I Z k · r × dS = (k × r) · dS = ∇ · (k × r) dV , using the prop ...
Unit 3. Integration 3A. Differentials, indefinite integration
... the top of Mt. Everest (10 km). b) Find the difference in pressure between the top and bottom of the Green Building. (Pretend it’s 100 meters tall starting at sea level.) Compute the numerical value using a calculator. Then use instead the linear approximation to ex near x = 0 to estimate the percen ...
... the top of Mt. Everest (10 km). b) Find the difference in pressure between the top and bottom of the Green Building. (Pretend it’s 100 meters tall starting at sea level.) Compute the numerical value using a calculator. Then use instead the linear approximation to ex near x = 0 to estimate the percen ...
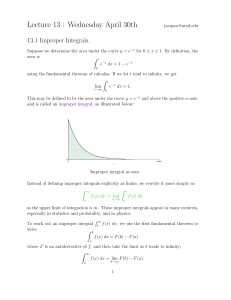
Lecture 13 : Wednesday April 30th
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
... 12.3 Other improper integrals In all the integrals so far, the functions we have dealt with are continuous on the range of integration. Another type of improper integral arises when the integrand is discontinuous over the range of integration, due to the presence of vertical asymptotes. For example, ...
Topics on Complex Geometry and Analysis
... Originally formulated in the 1970s, string theory hypothesizes that particles such as electrons and quarks are not actually point-like objects. Rather, if viewed through a very powerful microscope, those particles would look like little, tiny, closed loops of string. According to the theory, these s ...
... Originally formulated in the 1970s, string theory hypothesizes that particles such as electrons and quarks are not actually point-like objects. Rather, if viewed through a very powerful microscope, those particles would look like little, tiny, closed loops of string. According to the theory, these s ...
Calc2_RV1
... logarithmic function ln(x), the natural exponential functions exp(x) = ex, smooth curves, area, volume, arc-length and surface area; work done by a varying force or by a force exerted for varying ...
... logarithmic function ln(x), the natural exponential functions exp(x) = ex, smooth curves, area, volume, arc-length and surface area; work done by a varying force or by a force exerted for varying ...
MATH 212
... Second Graded Assignment. Complete solutions required for full credit. Due: May 19. (Numbers in parentheses are from 8 th edition.) Page 359: 87 (Page 357: 73) Page 361: 151 (Page 357: 75) Page 404:10; 11; 13 (Page 402: 8; 9; 10) Project Assignment. Do one of the following. Solution must be in print ...
... Second Graded Assignment. Complete solutions required for full credit. Due: May 19. (Numbers in parentheses are from 8 th edition.) Page 359: 87 (Page 357: 73) Page 361: 151 (Page 357: 75) Page 404:10; 11; 13 (Page 402: 8; 9; 10) Project Assignment. Do one of the following. Solution must be in print ...
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration.The Riemann integral is unsuitable for many theoretical purposes. Some of the technical deficiencies in Riemann integration can be remedied with the Riemann–Stieltjes integral, and most disappear with the Lebesgue integral.