ECO4112F Section 4 Integration
... xi = the value of x at each point ∑ = the sum of all the areas, starting from the first one (i = 1) and ending at the nth one (i = 1). Obviously this sum will not be a very accurate representation of the area. But perhaps if we make our Δx smaller, then this expression will become a more accurate re ...
... xi = the value of x at each point ∑ = the sum of all the areas, starting from the first one (i = 1) and ending at the nth one (i = 1). Obviously this sum will not be a very accurate representation of the area. But perhaps if we make our Δx smaller, then this expression will become a more accurate re ...
Lecture 17 - University of Chicago Math
... If you were paying close attention last lecture, you may have been wondering to yourself if there was a slicker way to evaluate definite integrals. Specifically, is there a formulaic way to find C? If you were paying any amount of attention, you will have noticed that the previous theorem we talked ...
... If you were paying close attention last lecture, you may have been wondering to yourself if there was a slicker way to evaluate definite integrals. Specifically, is there a formulaic way to find C? If you were paying any amount of attention, you will have noticed that the previous theorem we talked ...
4.1 Part 2 Particle Motion
... 4.3 Riemann Sums and Definite Integrals Definition of a Riemann Sum Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then ...
... 4.3 Riemann Sums and Definite Integrals Definition of a Riemann Sum Let f be defined on the closed interval [a, b] and let be a partition of [a, b] given by a = x0 < x1 < x2 < . . . < xn - 1 < xn = b, where xi is the length of the ith subinterval. If ci is any point in the ith subinterval, then ...
Test #3 Topics
... are assumed to be bounded by the graph of a positive function. Lecture In Section 2.1, we used the idea of instantaneous velocity to introduce the concept of a limit. In Section 3.1 (and again in Section 3.5) that idea was developed further to introduce the derivative. To compute the distance travel ...
... are assumed to be bounded by the graph of a positive function. Lecture In Section 2.1, we used the idea of instantaneous velocity to introduce the concept of a limit. In Section 3.1 (and again in Section 3.5) that idea was developed further to introduce the derivative. To compute the distance travel ...
Solutions for Exam 4
... may choose any six to do. Please write DON’T GRADE on the one that you don’t want me to grade. In writing your solution to each problem, include sufficient detail and use correct notation. (For instance, don’t forget to write “=” when you mean to say that two things are equal.) Your method of solving ...
... may choose any six to do. Please write DON’T GRADE on the one that you don’t want me to grade. In writing your solution to each problem, include sufficient detail and use correct notation. (For instance, don’t forget to write “=” when you mean to say that two things are equal.) Your method of solving ...
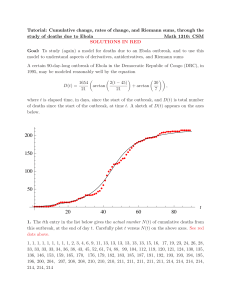
20 40 60 80 t 50 100 150 200
... The BIG IDEA behind what we’re seeing here (and behind the Fundamental Theorem of Calculus) is this. Suppose a quantity D(t) has a constant rate of change R over some interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your ...
... The BIG IDEA behind what we’re seeing here (and behind the Fundamental Theorem of Calculus) is this. Suppose a quantity D(t) has a constant rate of change R over some interval. Then total change in D(t) over the interval = rate of change R over the interval ⇥ length of interval (for example: if your ...
The Fundamental Theorem of Calculus and Integration
... Here, n is the number of rectangles used in the approximation, xi is the xvalue at the left-hand edge of each rectangle, and ∆x is the width of each rectangle. We concluded the lecture by saying that, in practice, we never compute this limit directly (though in some cases it is possible, and not too ...
... Here, n is the number of rectangles used in the approximation, xi is the xvalue at the left-hand edge of each rectangle, and ∆x is the width of each rectangle. We concluded the lecture by saying that, in practice, we never compute this limit directly (though in some cases it is possible, and not too ...
Math 223 - Vector Calculus (Fall 2016) Homework 4
... 2. (a) We have grad f = 3i + 4j . The value of the line integral will be maximised when the line goes in the same direction as grad f . Let r (t) = (2 + 3t)i + (1 + 4t)j be a parameterisation for the line starting at (2, 1) and going in the same direction as grad f . We want the distance from (2, 1) ...
... 2. (a) We have grad f = 3i + 4j . The value of the line integral will be maximised when the line goes in the same direction as grad f . Let r (t) = (2 + 3t)i + (1 + 4t)j be a parameterisation for the line starting at (2, 1) and going in the same direction as grad f . We want the distance from (2, 1) ...
Study guide for the third exam
... 5. The chain rule and integration by substitution (section 4.3) Be able to integrate a function like p0 (x)ep(x) where p(x) is a polynomial. We didn’t cover the more general algorithm for integration by substitution. ...
... 5. The chain rule and integration by substitution (section 4.3) Be able to integrate a function like p0 (x)ep(x) where p(x) is a polynomial. We didn’t cover the more general algorithm for integration by substitution. ...
Sample 3 - Trimble County Schools
... 7. Use the properties of sigma notation and the summation formulas evaluate the given ...
... 7. Use the properties of sigma notation and the summation formulas evaluate the given ...
Block 5 Stochastic & Dynamic Systems Lesson 14 – Integral Calculus
... interval [a,b] we divide the interval into n subintervals of equal width, x, and from each interval choose a point, xi*. Then the definite integral of f(x) from a to b is ...
... interval [a,b] we divide the interval into n subintervals of equal width, x, and from each interval choose a point, xi*. Then the definite integral of f(x) from a to b is ...
Document
... exists and does not depend on the choice of partitions or on the choice of the points in the subintervals. When this is the case we denote the limit by the symbol ...
... exists and does not depend on the choice of partitions or on the choice of the points in the subintervals. When this is the case we denote the limit by the symbol ...
On the number e, its irrationality, and factorials
... number of times. Therefore there can be no integers a and b for which 2 = a/b. All proofs that a number r is irrational follow this pattern of logic, called proof by contradiction: To prove that r is irrational we assume r = a/b for some integers a and b and then show (somehow) that this assumption ...
... number of times. Therefore there can be no integers a and b for which 2 = a/b. All proofs that a number r is irrational follow this pattern of logic, called proof by contradiction: To prove that r is irrational we assume r = a/b for some integers a and b and then show (somehow) that this assumption ...
Math 165 – worksheet for ch. 5, Integration – solutions
... Arguably, this is all we have to do for this problem (on an exam, we’d definitely count this as complete). But we can actually do a bit more: obviously, the rectangles making up the region which has area S, taken together, cover the region under the graph of 1/x, so ln(101) ≤ S. We could also consid ...
... Arguably, this is all we have to do for this problem (on an exam, we’d definitely count this as complete). But we can actually do a bit more: obviously, the rectangles making up the region which has area S, taken together, cover the region under the graph of 1/x, so ln(101) ≤ S. We could also consid ...
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. For many functions and practical applications, the Riemann integral can be evaluated by the fundamental theorem of calculus or approximated by numerical integration.The Riemann integral is unsuitable for many theoretical purposes. Some of the technical deficiencies in Riemann integration can be remedied with the Riemann–Stieltjes integral, and most disappear with the Lebesgue integral.