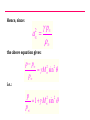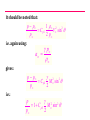Download Slide 1

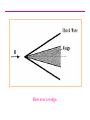
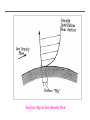
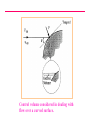
VELTECH Dr.RR &Dr.SR TECHNICAL UNIVERSITY
UEAEA43
HYPERSONIC AERODYNAMICS
PREPARED BY
Mr.S.Sivaraj
DEPARTMENT OF AERONAUTICAL
ASSISTANT PROFESSOR
UNIT - I
FUNDAMENTAL OF HYPERSONIC FLOWS
INTRODUCTION:
Hypersonic flow was loosely defined in the
Introduction as flow in which the Mach number is
greater than about 5. No real reasons were given at that
point as to why supersonic flows at high Mach numbers
were different from those at lower Mach numbers and
why, therefore, they had to have a different name.
However, it is the very existence of these differences that
really defines hypersonic flow. That is, hypersonic flows
are flows at such high Mach numbers that phenomena
arise that do not exist at lower supersonic Mach
numbers. The nature of these hypersonic flow
phenomena and, therefore, the real definition of what is
meant by hypersonic flow will be presented in the next
section.
Hypersonic flows, up to the present, have mainly
been associated with the reentry of orbiting and other
high altitude bodies into the atmosphere. For example, a
typical Mach number against altitude variation for a
reentering satellite is shown in the following figure. It
will be seen from this figure that because of the high
velocity that the craft had to possess to keep it in orbit,
very high Mach numbers - values that are well into the
hypersonic range – exist during reentry.
Typical variation of
mach number with
altitude during
reentry.
CHARACTERISTICS OF HYPERSONIC FLOW:
As mentioned above, hypersonic flows are usually
loosely described as flows at very high Mach numbers,
say greater than roughly 5. However, the real definition
of hypersonic flows are that they are flows at such high
Mach numbers that phenomena occur that do not exist at
low supersonic Mach numbers. These phenomena are
discussed in this section.
One of the characteristics of hypersonic flow is
the presence of an interaction between the oblique
shock wave generated at the leading edge of the body
and the boundary layer on the surface of the body.
Consider the oblique shock wave formed at the leading
edge of wedge in a supersonic flow as shown in the
following figure.
Flow over a wedge.
As the Mach number increases, the shock angle
decreases and the shock therefore lies very close to the
surface at high Mach numbers. This is illustrated in the
following figure.
Shock angle at
low and high
supersonic
Mach number
flow over a
wedge.
Because the shock wave lies close to the surface at
high Mach numbers, there is an interaction between the
shock wave and the boundary layer on the wedge surface.
In order to illustrate this shock wave-boundary layer
interaction, consider the flow of air over a wedge having
a half angle of 5 degrees at various Mach numbers. The
shock angle for any selected value of M can be obtained
from the oblique shock relations or charts. The angle
between the shock wave and the wedge surface is then
given by the difference between the shock angle and the
wedge half-angle. The variation of this angle with Mach
number is shown in the following figure.
Variation of
angle between
shock wave and
surface with
Mach number
for flow over a
wedge.
It will be seen from the above figure that, as the
Mach number increases, the shock wave lies closer and
closer to the surface.
Hypersonic flow normally only exists at relatively
low ambient pressures (high altitudes) which means
that the Reynolds numbers tend to be low and the
boundary layer thickness, therefore, tends to be
relatively large.
In hypersonic flow, then, the shock wave tends to
lie close to the surface and the boundary layer tends to
be thick. Interaction between the shock wave and the
boundary layer flow, as a consequence, usually occurs,
the shock being curved as a result and the flow
resembling that shown in the following figure.
Interaction between shock wave and boundary layer in
hypersonic flow over a wedge.
The above discussion used the flow over a wedge
to illustrate interaction between the shock wave and
the boundary layer flow in hypersonic flow. This
interaction occurs, in general, for all body shapes as
illustrated in the following figure.
Interaction between shock wave and boundary layer in
hypersonic flow over a curved body.
Another characteristic of hypersonic flows is the
high temperatures that are generated behind the shock
waves in such flows. In order to illustrate this, consider
flow through a normal shock wave occurring ahead of a
blunt body at a Mach number of 36 at an altitude of 59
km in the atmosphere. The flow situation is shown in
the following figure.
Normal shock wave
in situation
considered.
These were approximately
the conditions that occurred
during the reentry of some
of the earlier manned
spacecraft, the flow over
such a craft being illustrated
in the figure. The flow
situation shown in the
previous figure is therefore
an approximate model of the
situation shown in this
figure.
Flow over reentering spacecraft.
Conventional relationships for a normal shock wave at
a Mach number of 36 give:
T2
 253
T1
But at 59 km in atmosphere T = 258K (i.e., -15oC).
Hence, the conventional normal shock wave relations
give the temperature behind the shock wave as:
T2  258 x 253  65, 200K
At temperatures as high as these a number of socalled high temperature gas effects will become
important. For example, the values of the specific
heats cp and cv and their ratio  changes at higher
temperatures,
their
values
depending
on
temperature.
For example, the variation of the value of  of nitrogen
with temperature is shown in the following figure. It
will be seen from this figure that changes in  may
have to be considered at temperatures above about
500oC.
Variation of
specific heat ratio
of nitrogen with
temperature.
Another high-temperature effect arises from the
fact that, at ambient conditions, air is made up mainly
of nitrogen and oxygen in their diatomic form. At high
temperatures, these diatomic gases tend to dissociate
into their monatomic form and at still higher
temperatures, ionization of these monatomic atoms
tends to occur.
Dissociation occurs under the following circumstances:
For 2000 K  T  4000 K :
O2  2O
i.e., the oxygen molecules break down to O molecules.
For 4000 K  T  9000 K :
N2  2N
i.e., the nitrogen molecules break down to N molecules.
When such dissociation occurs, energy is
“absorbed”. It should also be clearly understood the
range of temperatures given indicates that the not all of
the air is immediately dissociated once a certain
temperature is reached. Over the temperature ranges
indicated above the air will, in fact, consist of a mixture
of diatomic and monatomic molecules, the fraction of
monatomic molecules increasing as the temperature
increases.
At still higher temperatures, ionization of the
monatomic oxygen and nitrogen will occur, i.e.:
For T  9000 K :
O  O   e
N  N   e
When ionization occurs, energy is again
“absorbed”. As with dissociation, ionization occurs over
a range of temperatures the air in this temperature
range consisting of a mixture of ionized and nonionized atoms, the fraction of ionized atoms increasing
as the temperature increases.
Other chemical changes can also occur at high
temperatures, e.g., there can be a reaction between the
nitrogen and the oxygen to form nitrous oxides at high
temperatures. This and the other effects mentioned
above are illustrated by the results given in the
following figure. This figure shows the variation of the
composition of air with temperature.
Variation of equilibrium
composition of air with
temperature.
It will be seen, therefore, that at high Mach
numbers, the temperature rise across a normal shock
may be high enough to cause specific heat changes,
dissociation, and, at very high Mach numbers,
ionization. As a result of these processes, conventional
shock relations do not apply. For example, as a result of
this for the conditions discussed above, i.e., for a normal
shock wave at a Mach number of 36 at an altitude of 59
km in the atmosphere, the actual temperature behind
the shock wave is approximately 11,000K rather than
the value of 65,200K indicated by the normal shock
relations for a perfect gas.
There are several other phenomena that are
often associated with high Mach number flow and
whose existence help define what is meant by a
hypersonic flow. For example, as mentioned above,
since most hypersonic flows occur at high altitudes the
presence of low density effects such as the existence of
“slip” at the surface, i.e., of a velocity jump at the
surface (see the following figure) is often taken as an
indication that hypersonic flow exists.
Surface slip in low-density flow.
UNIT - II
Simple Solution Methods For Hypersonic
In Viscid Flows
NEWTONIAN THEORY:
Although the details of the flow about a surface in
hypersonic flow are difficult to calculate due to the
complexity of the phenomena involved, the pressure
distribution about a surface placed in a hypersonic flow
can be estimated quite accurately using an approximate
approach that is discussed below. Because the flow
model assumed is essentially the same as one that was
incorrectly suggested by Newton for the calculation of
forces on bodies in incompressible flow, the model is
referred to as the Newtonian model.
First, consider the flow over a flat surface
inclined at an angle to a hypersonic flow. This flow
situation is shown in the following figure. Only the flow
over the upstream face of the surface will, for the
moment, be considered.
Hypersonic flow over a plane surface.
Because the shock waves lie so close to the surface in
hypersonic flow, the flow will essentially be unaffected
by the surface until the flow reaches the surface, i.e.,
until it “strikes” the surface, at which point it will
immediately become parallel to the surface. Hence, the
flow over the upstream face of a plane surface at
hypersonic speeds resembles that shown in the
following figure.
Newtonian model of hypersonic flow over a plane surface.
In order to find the pressure on the surface,
consider the momentum balance for the control volume
shown in the following figure.
Control volume considered.
Because the flow is all assumed to be turned
parallel to the surface at the surface, no momentum
leaves the control volume in the n direction so the force
on the control volume in this direction is equal to the
product of the rate mass enters the control volume and
the initial velocity component in the n direction i.e. is
given by:
mass flow rate x velocityin n-direction =
(V A sin  )V sin   V A sin 
2
Here, A is the area of the surface.
2
Now if p is the pressure acting on the upstream face of
the surface, the net force acting on the control volume in
the n direction is given by:
pA  p A
In deriving this result, it has been noted that since the
flow is not effected by the surface until it effectively
reaches the surface, the pressure on ABCDE (see
previous figure) is everywhere equal to p∞ and that the
forces on BC and DE are therefore equal and opposite
and cancel.
Combining the above two results then gives:
( p  p ) A  V A sin 
2
2
i.e. : p  p  V sin 
2
2
This result can be expressed in terms of a
dimensionless pressure coefficient, defined as before
by:
p p
Cp 
Using this gives:

1
V2
2
C p  2sin 
2
From the above analysis it follows that the
pressure coefficient is determined only by the angle of
the surface to the flow. The above analysis was for flow
over a flat surface. However, it will also apply to a
small portion of a curved surface such as that shown
in the following figure.
Control volume considered in dealing with
flow over a curved surface.
Therefore, the local pressure acting at any point on
the surface will be given as before by:
p  p
2
Cp 
 2sin 
1
2
V
2
This equation can be written as:
p  p    2 2
  V sin 
p
 p 
Hence, since:
 p
a 

2

the above equation gives:
p  p
2
2
  M  sin 
p
i.e.:
p
2
2
 1   M  sin 
p
FORCES ON A BODY: The Newtonian model gives the
pressure distribution on the upstream faces ( e.g. faces
AB and BC of the two-dimensional wedge shaped body
shown in the following figure) of a body in a hypersonic
flow to an accuracy that is acceptable for many
purposes. To find the net force acting on a body it is also
necessary to know the pressures acting on the
downstream faces of the body ( e.g., face AC of the body
shown in the following figure).
Two-dimensional
flow over a
wedged-shaped
body in hypersonic
flow.
As discussed above, in hypersonic flow, it is
effectively only when the flow reaches the surface that
it is influenced by the presence of the of the surface.
The flow that does not reach the surface is therefore
unaffected by the body. The flow leaving the upstream
faces of the body therefore turns parallel to the
original flow as shown in the following figure.
“Shadowed” areas of a body in hypersonic flow.
Since the flow is then all parallel to the original
flow direction and since the pressure in the outer part
of the flow that was not effected by the presence of the
body is p , the pressure throughout this downstream
flow will be p . From this it follows that the pressure
acting on the downstream faces of body in Newtonian
hypersonic flow is p . This is illustrated in the
following figure. The downstream faces on which the
pressure is p are often said to lie in the “shadow of
the freestream”.
In calculating the forces on a body in hypersonic flow
using the Newtonian model the pressure will be
assumed to be p on the downstream or “shadowed”
portions of the body surface. There are more
rigorous and elegant methods of arriving at this
assumption but the above discussion gives the basis
of the argument.
To illustrate how the pressure drag force on a
body is calculated using the Newtonian approach,
consider again flow over a two-dimensional wedge
shaped body shown in the following figure.
Pressures acting on faces of wedged-shaped body
The force on face AB of the body per unit width is
equal to pAB l where l is the length of AB. This
contributes pAB l sin β to the drag. But l sin β is equal
to W / 2, i.e., equal to the projected area of face AB.
Hence the pressure force on AB contributes pAB W / 2
to the drag.
Because the wedge is symmetrically placed with
respect to the freestream flow, the pressure on BC will
be equal to that on AB so the pressure force on BC will
also contribute pAB W / 2 to the drag.
Therefore, since AC is a shadowed surface on which
the pressure is assumed to be p , the drag on the
wedge per unit width is given by:
 p ABW
D  2
 2

  pW  ( p AB  p )W

The drag coefficient for the type of body being
considered is defined by:
CD 
D
1
2
V x Projected Area
2
But since unit width is being considered, the projected
area normal to the freestream flow direction is equal to
W, hence:
( p AB  p )W ( p AB  p )
CD 


1
1
1
2
2
2
V W
V W
V
2
2
2
D
It must be stressed that the above analysis only
gives the pressure drag on the surface. In general, there
will also be a viscous drag on the body. However, if the
body is relatively blunt, i.e., if the wedge angle is not
very small, the pressure drag will be much greater than
the viscous drag.
The drag on an axisymmetric body is calculated
using the same basic approach and the analysis of such
situations will not be discussed here.
MODIFIED NEWTONIAN THEORY:
Consider hypersonic flow over a symmetrical
body of arbitrary shape such as is shown in the
following figure.
Form of body being considered.
At any point on the surface, as shown above, the
pressure is given by:
p  p   V sin 
2
 
2
Hence at the “stagnation” point where θ = 90o and
where, therefore, sin θ = 1, the pressure, pS , is given
by:
pS  p   V
2
 
Hence:
pS  p
2
1
2
V
2
i.e., the pressure coefficient at the stagnation point is
given by:
C pS  2
From these relations it follows that the pressure
distribution about the surface can be written as:
Cp
C pS
 sin 2 
or as:
p  p
 sin 2 
pS  p
Now the Newtonian theory does not really apply
near the stagnation point. However, the shock wave in
this region is, as previously discussed, effectively a
normal shock wave. Therefore, the pressure on the
surface at the stagnation point can be found using
normal shock relations and then the Newtonian
relation can be used to determine the pressure
distribution around the rest of the body.
This means that the previous equation can be written
as:
Cp
C pSN
 sin 2 
where CpSN is the pressure coefficient at the stagnation
point as given by the normal shock relations. This is,
basically, the modified Newtonian equation.
Now it will be recalled that the normal shock relations
give:

pS

p
   1 2   1
 2 M  
 2
  1
2
   1 M     1


It is also noted that:
1
 1
p
1
p  p
p
Cp 

2
1

M

V2
2
2
Combining the above equations then gives:
C pSN



   1 2   1


M

2
 2





M




 1 / 

1
2 

  2



1
  1
2
M 



  1
    1

If M∞ is very large the above equation tends to:

C pSN 
   1   1
 2 
 2 
   1


1
 1
 
 
2
For γ = 1.4 this equation gives the limiting value of CpSN
for large values of M  ∞ as 1.839. Assuming a perfect
gas and a large freestream Mach number, the modified
Newtonian theory gives:
C p  1.839 sin 
2
As discussed in the first section of this chapter, when
the Mach number is very large, the temperature behind
the normal shock wave in the stagnation point region
becomes so large that high-temperature gas effects
become important and these affect the value of CpSN .
The relation between the perfect gas normal shock
results, the normal shock results with hightemperature effects accounted for and the Newtonian
result is illustrated by the typical results shown in the
following figure.
Typical variation of stagnation point pressure coefficient
with mach number.
The results shown in the above figure and
similar results for other situations indicate that the
stagnation pressure coefficient given by the high Mach
number form of the normal shock relations for a
perfect gas applies for Mach numbers above about 5
and that it gives results that are within 5% of the actual
values up to Mach numbers in excess of 10. Therefore,
the modified Newtonian equation using the high-Mach
number limit of the perfect gas normal shock to give
the stagnation point pressure coefficient will give
results that are of adequate accuracy for values of M∞
up to more than 10.
At higher values of M∞ , the unmodified
Newtonian equation gives more accurate results. Of
course, the modified Newtonian equation with the
stagnation pressure coefficient determined using hightemperature normal shock results will apply at all
hypersonic Mach numbers.
It should be noted that:
p  p
1  2 2
 C pS
V sin 
p
2 p
i.e. again using:
 p
a 

gives:
p  p
 2 2
 C pS M  sin 
p
2
i.e.:
p
 2 2
 1  C pS M  sin 
p
2
CONCLUDING REMARKS:
In hypersonic flow, because the temperatures
are very high and because the shock waves lie close to
the surface, the flow field is complex. However,
because the flow behind the shock waves is all
essentially parallel to the surface, the pressure
variation along a surface in a hypersonic flow can be
easily estimated using the Newtonian model. The
calculation of drag forces on bodies in hypersonic flow
using this method has been discussed.
CENTRIFUGAL FORCE CORRECTIONS
TO NEWTONIAN THEORY
Centrifugal force on a fluid element moving
along a curved streamline.
Shock layer model for centrifugal force
corrections to Newtonian theory.
Illustration of the tangent-wedge method.
Illustration of the tangent-cone method.
UNIT - III
Viscous Hypersonic Flow Theory
Boundary layer equation for hypersonic flow
2-D continuity Eqn
Boundary layer is very thin in comparison with the scale of the body
2-D continuity Eqn in non dimensional form
Because u varies from 0 at the wall to 1 at the edge of
the boundary layer, let us say that i7 is of the order of
magnitude equal to I, symbolized by 0A). Similarly,
i> = 0A). Also, since x varies from 0 to c, x = 0A).
However, since y varies from 0 to <5, where E < t, then v
is of the smaller order of magnitude, denoted by
y = 0(<5/c). Without loss of generality, we can assume
that c is a unit length. Therefore, y = 0C).
HYPERSONIC BOUNDARY LAYER THEORY:
SELF-SIMILAR SOLUTIONS
The boundary layer x-momentum
equation in terms of the transformed independent variables.
f is a stream function related to ψ
Transformed boundary layer x-momentum equation for a twodimensional, compressible flow.
The boundary layer y-momentum equation,
becomes in the transformed space
The boundary layer energy equation can also be transformed.
Defining a non dimensional static enthalpy as
where he is (the static enthalpy at the boundary layer edge, and utilizing the same
transformation as before
Qualitative sketches of non similar boundary layer profiles.
STRONG AND WEAK VISCOUS INTERACTIONS:
DEFINITION AND DESCRIPTION
Consider the sketch shown in Fig. which illustrates the hypersonic viscous
flow over a flat plate. Two regions of viscous interaction are illustrated here
the strong interaction region immediately downstream of the leading edge, and the
weak interaction region further downstream. By definition, the strong interaction
region is one where the following physical effects occur:
This mutual interaction process, where the boundary layer substantially affects
the inviscid flow, which in turn substantially affects the boundary layer, is called
a strong viscous interaction, as sketched in Fig.
Illustration of strong and weak viscous interactions.
The similarity parameter that governs laminar viscous interactions, both
strong and weak, is "chi bar," defined as
Schematic of the shock-wave/boundary-layer interaction.
THE NATURE OF HIGH-TEMPERATURE FLOWS
1. The thermodynamic properties (e, h, p, T, p, s, etc.) are completely different.
2. The transport properties (μ and k) are completely different. Moreover, the
additional transport mechanism of diffusion becomes important, with the
associated diffusion coefficients, Di,j.
3. High heat transfer rates are usually a dominant aspect of any high-temperahigh-temperature application.
4. The ratio of specific heats, γ = CP/CV, is a variable. In fact, for the analysis of
high-temperature flows, γ loses the importance it has for the classical constant
γ flows.
5. In view of the above, virtually all analyses of high temperature gas flows
require some type of numerical, rather than closed-form, solutions.
6. If the temperature is high enough to cause ionization, the gas becomes a
partially ionized plasma, which has a finite electrical conductivity. In turn, if
the flow is in the presence of an exterior electric or magnetic field, then
electromagnetic body forces act on the fluid elements. This is the purview of
an area called magneto hydrodynamics (MHD).
7. If the gas temperature is high enough, there will be nonadiabatic effects due
to radiation to or from the gas.
CHEMICAL EFFECTS IN AIR: THE VELOCITY-ALTITUDE MAP
Ranges of vibrational excitation, dissociation, and ionization for air
at I-aim pressure.
Velocity-amplitude map with superimposed regions of vibrational excitation,
dissociation, and ionization.