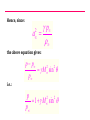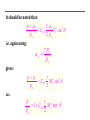* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slide 1
Drag (physics) wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Cnoidal wave wikipedia , lookup
Hydraulic jumps in rectangular channels wikipedia , lookup
Wind-turbine aerodynamics wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Stokes wave wikipedia , lookup
Coandă effect wikipedia , lookup
Flow measurement wikipedia , lookup
Lift (force) wikipedia , lookup
Boundary layer wikipedia , lookup
Airy wave theory wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Flow conditioning wikipedia , lookup
Reynolds number wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Fluid dynamics wikipedia , lookup
Aerodynamics wikipedia , lookup
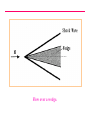
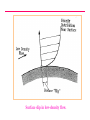
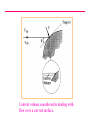
VELTECH Dr.RR &Dr.SR TECHNICAL UNIVERSITY UEAEA43 HYPERSONIC AERODYNAMICS PREPARED BY Mr.S.Sivaraj DEPARTMENT OF AERONAUTICAL ASSISTANT PROFESSOR UNIT - I FUNDAMENTAL OF HYPERSONIC FLOWS INTRODUCTION: Hypersonic flow was loosely defined in the Introduction as flow in which the Mach number is greater than about 5. No real reasons were given at that point as to why supersonic flows at high Mach numbers were different from those at lower Mach numbers and why, therefore, they had to have a different name. However, it is the very existence of these differences that really defines hypersonic flow. That is, hypersonic flows are flows at such high Mach numbers that phenomena arise that do not exist at lower supersonic Mach numbers. The nature of these hypersonic flow phenomena and, therefore, the real definition of what is meant by hypersonic flow will be presented in the next section. Hypersonic flows, up to the present, have mainly been associated with the reentry of orbiting and other high altitude bodies into the atmosphere. For example, a typical Mach number against altitude variation for a reentering satellite is shown in the following figure. It will be seen from this figure that because of the high velocity that the craft had to possess to keep it in orbit, very high Mach numbers - values that are well into the hypersonic range – exist during reentry. Typical variation of mach number with altitude during reentry. CHARACTERISTICS OF HYPERSONIC FLOW: As mentioned above, hypersonic flows are usually loosely described as flows at very high Mach numbers, say greater than roughly 5. However, the real definition of hypersonic flows are that they are flows at such high Mach numbers that phenomena occur that do not exist at low supersonic Mach numbers. These phenomena are discussed in this section. One of the characteristics of hypersonic flow is the presence of an interaction between the oblique shock wave generated at the leading edge of the body and the boundary layer on the surface of the body. Consider the oblique shock wave formed at the leading edge of wedge in a supersonic flow as shown in the following figure. Flow over a wedge. As the Mach number increases, the shock angle decreases and the shock therefore lies very close to the surface at high Mach numbers. This is illustrated in the following figure. Shock angle at low and high supersonic Mach number flow over a wedge. Because the shock wave lies close to the surface at high Mach numbers, there is an interaction between the shock wave and the boundary layer on the wedge surface. In order to illustrate this shock wave-boundary layer interaction, consider the flow of air over a wedge having a half angle of 5 degrees at various Mach numbers. The shock angle for any selected value of M can be obtained from the oblique shock relations or charts. The angle between the shock wave and the wedge surface is then given by the difference between the shock angle and the wedge half-angle. The variation of this angle with Mach number is shown in the following figure. Variation of angle between shock wave and surface with Mach number for flow over a wedge. It will be seen from the above figure that, as the Mach number increases, the shock wave lies closer and closer to the surface. Hypersonic flow normally only exists at relatively low ambient pressures (high altitudes) which means that the Reynolds numbers tend to be low and the boundary layer thickness, therefore, tends to be relatively large. In hypersonic flow, then, the shock wave tends to lie close to the surface and the boundary layer tends to be thick. Interaction between the shock wave and the boundary layer flow, as a consequence, usually occurs, the shock being curved as a result and the flow resembling that shown in the following figure. Interaction between shock wave and boundary layer in hypersonic flow over a wedge. The above discussion used the flow over a wedge to illustrate interaction between the shock wave and the boundary layer flow in hypersonic flow. This interaction occurs, in general, for all body shapes as illustrated in the following figure. Interaction between shock wave and boundary layer in hypersonic flow over a curved body. Another characteristic of hypersonic flows is the high temperatures that are generated behind the shock waves in such flows. In order to illustrate this, consider flow through a normal shock wave occurring ahead of a blunt body at a Mach number of 36 at an altitude of 59 km in the atmosphere. The flow situation is shown in the following figure. Normal shock wave in situation considered. These were approximately the conditions that occurred during the reentry of some of the earlier manned spacecraft, the flow over such a craft being illustrated in the figure. The flow situation shown in the previous figure is therefore an approximate model of the situation shown in this figure. Flow over reentering spacecraft. Conventional relationships for a normal shock wave at a Mach number of 36 give: T2 253 T1 But at 59 km in atmosphere T = 258K (i.e., -15oC). Hence, the conventional normal shock wave relations give the temperature behind the shock wave as: T2 258 x 253 65, 200K At temperatures as high as these a number of socalled high temperature gas effects will become important. For example, the values of the specific heats cp and cv and their ratio changes at higher temperatures, their values depending on temperature. For example, the variation of the value of of nitrogen with temperature is shown in the following figure. It will be seen from this figure that changes in may have to be considered at temperatures above about 500oC. Variation of specific heat ratio of nitrogen with temperature. Another high-temperature effect arises from the fact that, at ambient conditions, air is made up mainly of nitrogen and oxygen in their diatomic form. At high temperatures, these diatomic gases tend to dissociate into their monatomic form and at still higher temperatures, ionization of these monatomic atoms tends to occur. Dissociation occurs under the following circumstances: For 2000 K T 4000 K : O2 2O i.e., the oxygen molecules break down to O molecules. For 4000 K T 9000 K : N2 2N i.e., the nitrogen molecules break down to N molecules. When such dissociation occurs, energy is “absorbed”. It should also be clearly understood the range of temperatures given indicates that the not all of the air is immediately dissociated once a certain temperature is reached. Over the temperature ranges indicated above the air will, in fact, consist of a mixture of diatomic and monatomic molecules, the fraction of monatomic molecules increasing as the temperature increases. At still higher temperatures, ionization of the monatomic oxygen and nitrogen will occur, i.e.: For T 9000 K : O O e N N e When ionization occurs, energy is again “absorbed”. As with dissociation, ionization occurs over a range of temperatures the air in this temperature range consisting of a mixture of ionized and nonionized atoms, the fraction of ionized atoms increasing as the temperature increases. Other chemical changes can also occur at high temperatures, e.g., there can be a reaction between the nitrogen and the oxygen to form nitrous oxides at high temperatures. This and the other effects mentioned above are illustrated by the results given in the following figure. This figure shows the variation of the composition of air with temperature. Variation of equilibrium composition of air with temperature. It will be seen, therefore, that at high Mach numbers, the temperature rise across a normal shock may be high enough to cause specific heat changes, dissociation, and, at very high Mach numbers, ionization. As a result of these processes, conventional shock relations do not apply. For example, as a result of this for the conditions discussed above, i.e., for a normal shock wave at a Mach number of 36 at an altitude of 59 km in the atmosphere, the actual temperature behind the shock wave is approximately 11,000K rather than the value of 65,200K indicated by the normal shock relations for a perfect gas. There are several other phenomena that are often associated with high Mach number flow and whose existence help define what is meant by a hypersonic flow. For example, as mentioned above, since most hypersonic flows occur at high altitudes the presence of low density effects such as the existence of “slip” at the surface, i.e., of a velocity jump at the surface (see the following figure) is often taken as an indication that hypersonic flow exists. Surface slip in low-density flow. UNIT - II Simple Solution Methods For Hypersonic In Viscid Flows NEWTONIAN THEORY: Although the details of the flow about a surface in hypersonic flow are difficult to calculate due to the complexity of the phenomena involved, the pressure distribution about a surface placed in a hypersonic flow can be estimated quite accurately using an approximate approach that is discussed below. Because the flow model assumed is essentially the same as one that was incorrectly suggested by Newton for the calculation of forces on bodies in incompressible flow, the model is referred to as the Newtonian model. First, consider the flow over a flat surface inclined at an angle to a hypersonic flow. This flow situation is shown in the following figure. Only the flow over the upstream face of the surface will, for the moment, be considered. Hypersonic flow over a plane surface. Because the shock waves lie so close to the surface in hypersonic flow, the flow will essentially be unaffected by the surface until the flow reaches the surface, i.e., until it “strikes” the surface, at which point it will immediately become parallel to the surface. Hence, the flow over the upstream face of a plane surface at hypersonic speeds resembles that shown in the following figure. Newtonian model of hypersonic flow over a plane surface. In order to find the pressure on the surface, consider the momentum balance for the control volume shown in the following figure. Control volume considered. Because the flow is all assumed to be turned parallel to the surface at the surface, no momentum leaves the control volume in the n direction so the force on the control volume in this direction is equal to the product of the rate mass enters the control volume and the initial velocity component in the n direction i.e. is given by: mass flow rate x velocityin n-direction = (V A sin )V sin V A sin 2 Here, A is the area of the surface. 2 Now if p is the pressure acting on the upstream face of the surface, the net force acting on the control volume in the n direction is given by: pA p A In deriving this result, it has been noted that since the flow is not effected by the surface until it effectively reaches the surface, the pressure on ABCDE (see previous figure) is everywhere equal to p∞ and that the forces on BC and DE are therefore equal and opposite and cancel. Combining the above two results then gives: ( p p ) A V A sin 2 2 i.e. : p p V sin 2 2 This result can be expressed in terms of a dimensionless pressure coefficient, defined as before by: p p Cp Using this gives: 1 V2 2 C p 2sin 2 From the above analysis it follows that the pressure coefficient is determined only by the angle of the surface to the flow. The above analysis was for flow over a flat surface. However, it will also apply to a small portion of a curved surface such as that shown in the following figure. Control volume considered in dealing with flow over a curved surface. Therefore, the local pressure acting at any point on the surface will be given as before by: p p 2 Cp 2sin 1 2 V 2 This equation can be written as: p p 2 2 V sin p p Hence, since: p a 2 the above equation gives: p p 2 2 M sin p i.e.: p 2 2 1 M sin p FORCES ON A BODY: The Newtonian model gives the pressure distribution on the upstream faces ( e.g. faces AB and BC of the two-dimensional wedge shaped body shown in the following figure) of a body in a hypersonic flow to an accuracy that is acceptable for many purposes. To find the net force acting on a body it is also necessary to know the pressures acting on the downstream faces of the body ( e.g., face AC of the body shown in the following figure). Two-dimensional flow over a wedged-shaped body in hypersonic flow. As discussed above, in hypersonic flow, it is effectively only when the flow reaches the surface that it is influenced by the presence of the of the surface. The flow that does not reach the surface is therefore unaffected by the body. The flow leaving the upstream faces of the body therefore turns parallel to the original flow as shown in the following figure. “Shadowed” areas of a body in hypersonic flow. Since the flow is then all parallel to the original flow direction and since the pressure in the outer part of the flow that was not effected by the presence of the body is p , the pressure throughout this downstream flow will be p . From this it follows that the pressure acting on the downstream faces of body in Newtonian hypersonic flow is p . This is illustrated in the following figure. The downstream faces on which the pressure is p are often said to lie in the “shadow of the freestream”. In calculating the forces on a body in hypersonic flow using the Newtonian model the pressure will be assumed to be p on the downstream or “shadowed” portions of the body surface. There are more rigorous and elegant methods of arriving at this assumption but the above discussion gives the basis of the argument. To illustrate how the pressure drag force on a body is calculated using the Newtonian approach, consider again flow over a two-dimensional wedge shaped body shown in the following figure. Pressures acting on faces of wedged-shaped body The force on face AB of the body per unit width is equal to pAB l where l is the length of AB. This contributes pAB l sin β to the drag. But l sin β is equal to W / 2, i.e., equal to the projected area of face AB. Hence the pressure force on AB contributes pAB W / 2 to the drag. Because the wedge is symmetrically placed with respect to the freestream flow, the pressure on BC will be equal to that on AB so the pressure force on BC will also contribute pAB W / 2 to the drag. Therefore, since AC is a shadowed surface on which the pressure is assumed to be p , the drag on the wedge per unit width is given by: p ABW D 2 2 pW ( p AB p )W The drag coefficient for the type of body being considered is defined by: CD D 1 2 V x Projected Area 2 But since unit width is being considered, the projected area normal to the freestream flow direction is equal to W, hence: ( p AB p )W ( p AB p ) CD 1 1 1 2 2 2 V W V W V 2 2 2 D It must be stressed that the above analysis only gives the pressure drag on the surface. In general, there will also be a viscous drag on the body. However, if the body is relatively blunt, i.e., if the wedge angle is not very small, the pressure drag will be much greater than the viscous drag. The drag on an axisymmetric body is calculated using the same basic approach and the analysis of such situations will not be discussed here. MODIFIED NEWTONIAN THEORY: Consider hypersonic flow over a symmetrical body of arbitrary shape such as is shown in the following figure. Form of body being considered. At any point on the surface, as shown above, the pressure is given by: p p V sin 2 2 Hence at the “stagnation” point where θ = 90o and where, therefore, sin θ = 1, the pressure, pS , is given by: pS p V 2 Hence: pS p 2 1 2 V 2 i.e., the pressure coefficient at the stagnation point is given by: C pS 2 From these relations it follows that the pressure distribution about the surface can be written as: Cp C pS sin 2 or as: p p sin 2 pS p Now the Newtonian theory does not really apply near the stagnation point. However, the shock wave in this region is, as previously discussed, effectively a normal shock wave. Therefore, the pressure on the surface at the stagnation point can be found using normal shock relations and then the Newtonian relation can be used to determine the pressure distribution around the rest of the body. This means that the previous equation can be written as: Cp C pSN sin 2 where CpSN is the pressure coefficient at the stagnation point as given by the normal shock relations. This is, basically, the modified Newtonian equation. Now it will be recalled that the normal shock relations give: pS p 1 2 1 2 M 2 1 2 1 M 1 It is also noted that: 1 1 p 1 p p p Cp 2 1 M V2 2 2 Combining the above equations then gives: C pSN 1 2 1 M 2 2 M 1 / 1 2 2 1 1 2 M 1 1 If M∞ is very large the above equation tends to: C pSN 1 1 2 2 1 1 1 2 For γ = 1.4 this equation gives the limiting value of CpSN for large values of M ∞ as 1.839. Assuming a perfect gas and a large freestream Mach number, the modified Newtonian theory gives: C p 1.839 sin 2 As discussed in the first section of this chapter, when the Mach number is very large, the temperature behind the normal shock wave in the stagnation point region becomes so large that high-temperature gas effects become important and these affect the value of CpSN . The relation between the perfect gas normal shock results, the normal shock results with hightemperature effects accounted for and the Newtonian result is illustrated by the typical results shown in the following figure. Typical variation of stagnation point pressure coefficient with mach number. The results shown in the above figure and similar results for other situations indicate that the stagnation pressure coefficient given by the high Mach number form of the normal shock relations for a perfect gas applies for Mach numbers above about 5 and that it gives results that are within 5% of the actual values up to Mach numbers in excess of 10. Therefore, the modified Newtonian equation using the high-Mach number limit of the perfect gas normal shock to give the stagnation point pressure coefficient will give results that are of adequate accuracy for values of M∞ up to more than 10. At higher values of M∞ , the unmodified Newtonian equation gives more accurate results. Of course, the modified Newtonian equation with the stagnation pressure coefficient determined using hightemperature normal shock results will apply at all hypersonic Mach numbers. It should be noted that: p p 1 2 2 C pS V sin p 2 p i.e. again using: p a gives: p p 2 2 C pS M sin p 2 i.e.: p 2 2 1 C pS M sin p 2 CONCLUDING REMARKS: In hypersonic flow, because the temperatures are very high and because the shock waves lie close to the surface, the flow field is complex. However, because the flow behind the shock waves is all essentially parallel to the surface, the pressure variation along a surface in a hypersonic flow can be easily estimated using the Newtonian model. The calculation of drag forces on bodies in hypersonic flow using this method has been discussed. CENTRIFUGAL FORCE CORRECTIONS TO NEWTONIAN THEORY Centrifugal force on a fluid element moving along a curved streamline. Shock layer model for centrifugal force corrections to Newtonian theory. Illustration of the tangent-wedge method. Illustration of the tangent-cone method. UNIT - III Viscous Hypersonic Flow Theory Boundary layer equation for hypersonic flow 2-D continuity Eqn Boundary layer is very thin in comparison with the scale of the body 2-D continuity Eqn in non dimensional form Because u varies from 0 at the wall to 1 at the edge of the boundary layer, let us say that i7 is of the order of magnitude equal to I, symbolized by 0A). Similarly, i> = 0A). Also, since x varies from 0 to c, x = 0A). However, since y varies from 0 to <5, where E < t, then v is of the smaller order of magnitude, denoted by y = 0(<5/c). Without loss of generality, we can assume that c is a unit length. Therefore, y = 0C). HYPERSONIC BOUNDARY LAYER THEORY: SELF-SIMILAR SOLUTIONS The boundary layer x-momentum equation in terms of the transformed independent variables. f is a stream function related to ψ Transformed boundary layer x-momentum equation for a twodimensional, compressible flow. The boundary layer y-momentum equation, becomes in the transformed space The boundary layer energy equation can also be transformed. Defining a non dimensional static enthalpy as where he is (the static enthalpy at the boundary layer edge, and utilizing the same transformation as before Qualitative sketches of non similar boundary layer profiles. STRONG AND WEAK VISCOUS INTERACTIONS: DEFINITION AND DESCRIPTION Consider the sketch shown in Fig. which illustrates the hypersonic viscous flow over a flat plate. Two regions of viscous interaction are illustrated here the strong interaction region immediately downstream of the leading edge, and the weak interaction region further downstream. By definition, the strong interaction region is one where the following physical effects occur: This mutual interaction process, where the boundary layer substantially affects the inviscid flow, which in turn substantially affects the boundary layer, is called a strong viscous interaction, as sketched in Fig. Illustration of strong and weak viscous interactions. The similarity parameter that governs laminar viscous interactions, both strong and weak, is "chi bar," defined as Schematic of the shock-wave/boundary-layer interaction. THE NATURE OF HIGH-TEMPERATURE FLOWS 1. The thermodynamic properties (e, h, p, T, p, s, etc.) are completely different. 2. The transport properties (μ and k) are completely different. Moreover, the additional transport mechanism of diffusion becomes important, with the associated diffusion coefficients, Di,j. 3. High heat transfer rates are usually a dominant aspect of any high-temperahigh-temperature application. 4. The ratio of specific heats, γ = CP/CV, is a variable. In fact, for the analysis of high-temperature flows, γ loses the importance it has for the classical constant γ flows. 5. In view of the above, virtually all analyses of high temperature gas flows require some type of numerical, rather than closed-form, solutions. 6. If the temperature is high enough to cause ionization, the gas becomes a partially ionized plasma, which has a finite electrical conductivity. In turn, if the flow is in the presence of an exterior electric or magnetic field, then electromagnetic body forces act on the fluid elements. This is the purview of an area called magneto hydrodynamics (MHD). 7. If the gas temperature is high enough, there will be nonadiabatic effects due to radiation to or from the gas. CHEMICAL EFFECTS IN AIR: THE VELOCITY-ALTITUDE MAP Ranges of vibrational excitation, dissociation, and ionization for air at I-aim pressure. Velocity-amplitude map with superimposed regions of vibrational excitation, dissociation, and ionization.