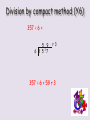Download Maths Workshop KS1

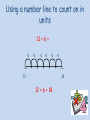
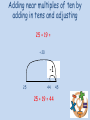
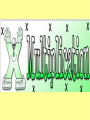
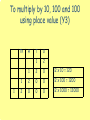
Maths Workshop
KS1
Aims in KS1
• To have a secure knowledge of number
facts and a clear understanding of the
four operations.
• To be able to use their knowledge and
understanding to carry out calculations
mentally and to apply appropriate
strategies when using larger numbers.
• To have an efficient, reliable written
method of calculation for each operation
that can applied with confidence.
Strategies for Mental
Calculations
• Number bonds to 10 and 20
• Counting forwards and backwards in 1s
and 10s
• Doubles and near doubles
• Partitioning and recombining numbers
• Adjusting near multiples of 10
• Bridging through 10
• Inverse relationships
Addition
Progression in Addition
Recording calculations in pictures
4+2= 6
3+3=6
Bead strings or beads / counters
to illustrate addition
8 + 2 = 10
Using a number line to count on in
units
12 + 6 =
+1
+1 +1
+1 +1
+1 +1
+1 +1
+1 +1
+1
12
12
+ 6 = 18
12 + 6 12
= 18
18
18
Using a number line to count on in
tens
24 + 30 =
+
10
+ 10
24
10
++10
34
++ 10
10
44
24 + 30 = 54
54
Partition a number to bridge
through a multiple of ten
I can partition a number to bridge through a multiple of ten
16++87 =
15
+ 5+ 4
16
15
++33
20
20
23
23
15 + 8 = 23
rtition
a
number
to
bridge
through
a
multipl
Use a number line to count on in
16
+
7
tens and units by partitioning
48 + 14 =
++ 43
++ 10
4
48
16
58
20
48 + 14 = 62
62
23
Adding near multiples of ten by
adding in tens and adjusting
25 + 19 =
+ 20
-1
35
25
54
44
5545
25 + 19 = 44
Partitioning to solve more
complex addition
265 + 177 =
265 = 200 + 60 + 5
177 = 100 + 70 + 7
__________
300 + 130 + 12
= 442
Using the partitioned method to
add in columns
215 + 176 =
215
+ 176
11 ( 5 + 6)
80 (10 + 70)
300 (200 + 100)
391
215 + 176 = 391
Column method including carrying
digits
217 + 179 =
217
179
39 6
1
217 + 179 = 396
Bead strings or beads / counters
to illustrate subtraction
10 – 2 = 8
Using a number line to count back
in units
18 - 6 =
+1
-1 +1
-1 +1
-1 +1
-1 +1
-1 +1
-1
12
12
12 + 6 =1818
– 6 = 12
1818
Progression in Subtraction
Recording calculations in pictures
9–5=4
To find the difference by
counting on the number line
32 - 18 =
+
10 ++ 10
2
+ 210
++10
2 + 10 + 2 = 14
18
20
30
32 - 18 = 14
32
To bridge through a multiples of
ten when counting back
42 – 25 =
+ 10
+- 10
2
-3
17
20
+- 20
10
22
42 – 25 = 17
42
To subtract near multiples of ten
by subtracting in tens and
adjusting
55 – 19 =
- 20
+1
35
36
55 – 19 = 36
55
Ic
To partition numbers and subtract
using decomposition
81 – 57 =
70 1
80 1
50 7
20 4
81 – 57 = 24
To partition numbers and subtract
using decomposition
534 - 218 =
20
1
534 = 500 30 4
218 = 200 10 8
300 10 6
534 - 218 = 316
To use a number line to find the
difference between decimals
6.2 – 1.6 =
10
++
0.4
1.6
++410
2.0
++ 10
0.2
6.0
6.2 – 1.6 = 4.6
0.4 + 4 + 0.2 = 4.6
6.2
Subtraction using the column
method
561 – 146 =
51
561
146
415
561 – 146 = 415
Counting objects in equal groups
Count how many in each group
3 groups /lots of 5
To understand multiplication as
repeated addition
5 lots of 2 =
2+2+2+2+2=
5 x 2 = 10
5 x 2 = 10
Multiplication as arrays
(arranging the counters in equal
rows – an array)
Repeated addition on a number
line
4 lots of 5 =
0
5
10
15
20
4 x55+=520
+ 5 + 5 = 20
4 lots of 5
or
4 x 5 = 20
To count in 2s, 5s and 10s
2s
5s
10s
To simplify multiplication by
partitioning
14 x 3 =
(14 = 10 + 4)
10 x 3 = 30
4 x 3 = 12
14 x 3 = 42
(30 + 12 = 42)
To multiply by 10, 100 and 100
using place value (Y3)
Th
1
H
T
U
1
2
1
2
0
12 x 10 = 120
1
2
0
0
12 x 100 = 1200
2
0
0
0
12 x 1000 = 12000
To multiply using multiples of 10,
100, 1000
3 x 20 =
3 x 2 x 10 = 60
7 x 300 =
7 x 3 x 100 = 2100
To multiply using grid method (Y4)
24 x 6 =
x
20
4
6
120
24
120 + 24 = 144
24 x 6 = 144
Multiply by expanded
multiplication
42 x 8 =
42
x 8
16 (2 x 8)
320 (40 x 8)
336
42 x 8 = 336
Multiplication using column method
(Y5)
24 x 37 =
24
x 37
168
720
888
24 x 37 = 888
Sharing items into groups
6 shared between 2 is 3
Division by repeated subtraction
20 ÷ 5 =
-5
0
-5
5
-5
10
-5
15
4 x 5 = 20
20 ÷ 5 = 4
20
Division by chunking (Y4-5)
63 ÷ 5 =
63
50 (10 X 5)
13 ( 2 x 5 )
10
3
63 ÷ 5 = 12 r 3
Division by semi-compact division (Y6)
357 ÷ 6 =
59
6 357
30
57
54
3
357 ÷ 6 = 59 r 3
Division by compact method (Y6)
357 ÷ 6 =
5 9
6 3 5 57
r3
357 ÷ 6 = 59 r 3
Questions