* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Atomic orbital wikipedia , lookup
Planck's law wikipedia , lookup
EPR paradox wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Boson sampling wikipedia , lookup
Bell's theorem wikipedia , lookup
Quantum entanglement wikipedia , lookup
Quantum group wikipedia , lookup
Bell test experiments wikipedia , lookup
Density matrix wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum machine learning wikipedia , lookup
Coherent states wikipedia , lookup
Hidden variable theory wikipedia , lookup
Electron configuration wikipedia , lookup
Tight binding wikipedia , lookup
Quantum state wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Canonical quantization wikipedia , lookup
Double-slit experiment wikipedia , lookup
History of quantum field theory wikipedia , lookup
Chemical bond wikipedia , lookup
Hydrogen atom wikipedia , lookup
Quantum teleportation wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Atomic theory wikipedia , lookup
Quantum key distribution wikipedia , lookup
Population inversion wikipedia , lookup
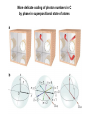
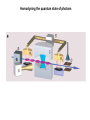
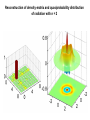
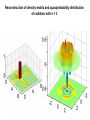
MANIPULATING THE QUANTUM STATE OF SINGLE ATOMS AND PHOTONS works of Nobel Laureates in physics 2012 A.V.Masalov Lebedev Physics Institute, RAS, Moscow [email protected] фото Nobel Prize in Physics 2012: Serge HAROCHE and David J. WINELAND "FOR GROUND-BREAKING EXPERIMENTAL METHODS THAT ENABLE MEASURING AND MANIPULATION OF INDIVIDUAL QUANTUM SYSTEMS“ PHOTONS IONS Serge HAROCHE École Normale Supérieure, Paris, France MANIPULATING THE QUANTUM STATE OF SINGLE PHOTONS INDIVIDUAL QUANTUM SYSTEMS: photons of electromagnetic field @ 51.1 ГГц ( ~ 6 mm); number of photons – from 1 to about 10. MEASURING AND MANIPULATION: by means of single atoms in superpositional states. SUPERCONDUCTING CAVITIES: - Open Fabry Perot - Niobium on diamond machined copper - Unprecedented lifetime @ 51 GHz, 0.8 K : Tc = 0,13 s Q = 4,2 × 1010 F = 4,6 × 109 !!! Average number of thermal photons ~ 0.05 CIRCULAR RYDBERG ATOMS: - Long lifetime (30 ms) - Millimeter-wave transitions - Tunable via the Stark effect - Large coupling to radiation - Efficient and state-selective single-atom detection !!! Excitation to superpositional n=3 n=2 n=1 n=0 states (by ‘’-pulse of light): g e B – atomic source (beam of single Rb atoms) selected by velositiy: ~ 900 pc/s, ~ 250 m/s. С – superconducting resonator: 51.1 GHz, 0.8 K, tunable (!) R1 и R2 – auxilary resonator for excitation anf analysis of atoms. S – source of radiation at about 51 GHz. D – detector of atomic state: g or e . Source R1 ‘’-pulse atom g e Main resonator C tuned close but out of resonance with atoms Atoms are exposed to Stark-shift of levels in the interaction area C: Atom + 1 photon: Source R2 ‘’-pulse g e g ei e atom + 1 photon ei 1 pure exited state! atom + 0 photon INTERFEROMETER RAMSEY 0 pure ground state! SINGLE PHOTON IN RESONATOR Photon decay in resonator: 1 realization 5 realizations 15 realizations 904 realizations INTERFEROMETER RAMSEY The ‘door’ from classical world to quantum one: ‘’-pulse The ‘door’ from quantum world to classical one: interferometer Ramsey g e g e g e More delicate coding of photon numbers in resonator by phase in superpositional state of atoms Number of photons Atomic state 2 /8 Atomic state out of Ramsey interferometer 0 0 g ei 0 e g 0 e 1 1 0 g ei1 e g sin e cos 2 0 g ei 2 e g sin 2 e cos 2 3 0 g ei 3 e g sin3 e cos3 4 0 g ei 4 e g sin 4 e cos 4 5 0 g ei 5 e g sin5 e cos5 6 0 g ei 6 e g sin 6 e cos6 7 0 g ei 7 e g sin 7 e cos7 More delicate coding of photon numbers in C by phase in superpositional state of atoms 1. Photon-state preparation in C by resonant atoms. 2. Photon-state detection by non-resonant atoms: QUANTUM NON-DEMOLITION MEASUREMENTS OF PHOTON NUMBER IN RESONATOR POISSON DISTRIBUTION OF PHOTONS (at final stage on measurements) TRACING THE NUMBER OF PHOTONS IN RESONATOR Homodyning the quantum state of photons Reconstruction of density-matrix and quasiprobability distribution of radiation with n = 1 Reconstruction of density-matrix and quasiprobability distribution of radiation with n = 2 Reconstruction of density-matrix and quasiprobability distribution of radiation with n = 3 Reconstruction of density-matrix and quasiprobability distribution of radiation with n = 4 Reconstruction of density-matrix and quasiprobability distribution of radiation in the states of ‘Schredinger-cat’ even odd decoherence END «Время жизни» одного фотона (кр) и нуля фотонов (син)