* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download L07_Synchrotron_Radiation
Introduction to quantum mechanics wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Photoelectric effect wikipedia , lookup
Old quantum theory wikipedia , lookup
Future Circular Collider wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Electron scattering wikipedia , lookup
Photon polarization wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
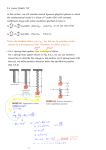
AXEL-2011 Introduction to Particle Accelerators Synchrotron Radiation What is it ? Rate of energy loss Longitudinal damping Transverse damping Quantum fluctuations Wigglers Rende Steerenberg (BE/OP) 13 January 2011 Acceleration and Electro-Magnetic Radiation An accelerating charge emits Electro-Magnetic waves. Example: An antenna is fed by an oscillating current and it emits electro magnetic waves. In our accelerator we know to types of acceleration: Longitudinal – RF system Transverse – Magnetic fields, dipoles, quadrupoles, etc.. Force due to magnetic field gives change of direction dp d ( m v ) m a F dt dt Momentum change So: m v constant R. Steerenberg, 13-Jan-2011 Newton’s law Direction changes but not magnitude AXEL - 2011 2 Rate of EM radiation The rate at which a relativistic lepton radiates EM energy is : Force // velocity Longitudinal square of energy (E2) Force velocity Transverse square of magnetic field (B2) PSR E2 B2 In our accelerators: Transverse force > Longitudinal force Therefore we only consider radiation due to ‘transverse acceleration’ (thus magnetic forces) R. Steerenberg, 13-Jan-2011 AXEL - 2011 3 Rate of energy loss (1) This EM radiation generates an energy loss of the particle concerned, which can be calculated using: constant 2 rc P 3 m c 2 0 E F 2 3 2 Electron radius Velocity of light Total energy ‘Accelerating’ force Lepton rest mass Our force can be written as: F = evB = ecB 2 e rc Thus: P 3 m c 2 3 2 0 3 E B 2 p E but ( B ) e ec 2 2 rc Which gives us: P 3 m c 2 0 R. Steerenberg, 13-Jan-2011 3 E AXEL - 2011 4 v 1 c 2 4 Rate of energy loss (2) 2 rc P We have: 3 m c 2 0 3 E 4 2 ,which gives the energy loss We are interested in the energy loss per revolution for which we need to integrate the above over 1 turn ds Bending radius Thus: Pdt P inside the magnets c ds d However: 2 c c Lepton energy 4 r 4 1 E 2 d Finally this gives: u 3 2 3 m0 c Gets very large if E is large !!! C R. Steerenberg, 13-Jan-2011 AXEL - 2011 CE 4 5 What about the synchrotron oscillations ? The RF system, besides increasing the energy has to make up for this energy loss u. All the particles with the same phase, , w.r.t. RF waveform will have the same energy gain E = Vsin However, Lower energy particles lose less energy per turn Higher energy particles lose more energy per turn u CE What will happen…??? R. Steerenberg, 13-Jan-2011 AXEL - 2011 6 4 Synchrotron motion for leptons E u CE 4 t (or ) All three particles will gain the same energy from the RF system The black particle will lose more energy than the red one. This leads to a reduction in the energy spread, since u varies with E4. R. Steerenberg, 13-Jan-2011 AXEL - 2011 7 Longitudinal damping in numbers (1) Remember how we calculated the synchrotron frequency. It was based on the change in energy: dE V sin Now we have to add an extra term, the energy loss du dE V sin du becomes dE frevV sin frev du dt Our equation for the synchrotron oscillation becomes then: Extra term for d 2 h 2 h 2 2 f V f rev rev du 0 2 E dt E 2 R. Steerenberg, 13-Jan-2011 AXEL - 2011 energy loss 8 Longitudinal damping in numbers (2) This term: 2 h f rev 2 du E Can be written as: 2 h f This now becomes: du du dE E dE E 2 rev du dE but dE E dE 1 df E f rev rev du 2 h df f dE rev du 1 d dE T dt rev 1 d T dt The synchrotron oscillation differential equation becomes now: Damped SHM, rev rev d du 1 d 2 h 2 f rev V 0 2 dt dE Trev dt E 2 R. Steerenberg, 13-Jan-2011 AXEL - 2011 as expected 9 Longitudinal damping in numbers (3) So, we have: d 2 du 1 d 2 h 2 f V 0 rev 2 dt dE Trev dt E The damping coefficient du 1 dE T rev This confirms that the variation of u as a function of E leads to damping of the synchrotron oscillations as we already expected from our reasoning on the 3 particles in the longitudinal phase space. R. Steerenberg, 13-Jan-2011 AXEL - 2011 10 Longitudinal damping time du 1 dE T CE du 4CE We know that u and thus dE CE du 4u Not totally So approximately: u correct since dE E E The damping coefficient is given by: rev 4 3 4 For the damping time we have then: Energy 1 ET Damping time = 4u rev Revolution time CE 4 Energy loss/turn The damping time decreases rapidly (E3) as we increase the beam energy. R. Steerenberg, 13-Jan-2011 AXEL - 2011 11 Damping & Longitudinal emittance Damping of the energy spread leads to shortening of the bunches and hence a reduction of the longitudinal emittance. E Initial Later… E d R. Steerenberg, 13-Jan-2011 AXEL - 2011 12 Some LHC numbers Energy loss per turn at: injection at 450 GeV = 1.15 x 10-1 eV Collision at 7 TeV = 6.71 x 103 eV Power loss per meter in the main dipoles at 7 TeV is 0.2 W/m Longitudinal damping time at: Injection at 450 GeV = 48489.1 hours Collision at 7 TeV = 13 hours R. Steerenberg, 13-Jan-2011 AXEL - 2011 13 What about the betatron oscillations ? (1) Each photon emission reduces the transverse and longitudinal energy or momentum. Lets have a look in the vertical plane: Emitted photon (dp) total momentum (p) momentum lost dp ideal trajectory particle R. Steerenberg, 13-Jan-2011 particle trajectory AXEL - 2011 14 What about the betatron oscillations ? (2) The RF system must make up for the loss in longitudinal energy dE or momentum dp. However, the cavity only supplies energy parallel to ideal trajectory. ideal trajectory new particle trajectory old particle trajectory Each passage in the cavity increases only the longitudinal energy. This leads to a direct reduction of the amplitude of the betatron oscillation. R. Steerenberg, 13-Jan-2011 AXEL - 2011 15 Vertical damping in numbers (1) The RF system increases the momentum p by dp or energy E by dE Tan(α)= α pt = transverse momentum pT= total momentum If α << pt y' p p = longitudinal momentum dp is small pt pt dp dp new( y ' ) 1 y ' 1 p dp p p p The change in transverse angle is thus given by: dp dE dy' y ' y' p E R. Steerenberg, 13-Jan-2011 AXEL - 2011 16 Vertical damping in numbers (2) A change in the transverse angle alters the betatron oscillation amplitude y’ a.sin da .dy'.sin dE da . y ' .sin E dE da . y ' .sin E dE da a sin E 2 y dy’ 0 2 2 0 a da da 1 dE a 2 E Summing over many photon emissions R. Steerenberg, 13-Jan-2011 AXEL - 2011 17 Vertical damping in numbers (3) We found: dE is just the change in energy per turn u (energy given back by RF) da 1 dE a 2 E da a The change in amplitude/turn is thus: u a Which is also: a 2E da u Thus: a dt 2 ET Change in amplitude/second Revolution time This shows exponential damping with coefficient: 2 ET Damping time = u R. Steerenberg, 13-Jan-2011 u 2ET (similar to longitudinal case) AXEL - 2011 CE 4 18 Horizontal damping in numbers da 1u Vertically we found: a 2E This is still valid horizontally However, in the horizontal plane, when a particle changes energy (dE) its horizontal position changes too OK since =1 dr dp dE u p p p r p E E is related to D(s) in the bending magnets da u 1 2 horizontally we get: a 2E 2 ET 1 Horizontal damping time: u 1 2 R. Steerenberg, 13-Jan-2011 AXEL - 2011 19 Some intermediate remarks…. Transverse damping for LHC time at: Injection at 450 GeV = 48489.1 hours Collision at 7 TeV = 26 hours Longitudinal and transverse emittances all shrink as a function of time. For leptons damping times are typically a few milliseconds up to a few seconds. Advantages: Reduction in losses Injection oscillations are damped out Allows easy accumulation Instabilities are damped Inconvenience: Lepton machines need lots of RF power, therefore LEP was stopped All damping is due to the energy gain from the RF system an not due to the emission of synchrotron radiation R. Steerenberg, 13-Jan-2011 AXEL - 2011 20 Is there a limit to this damping ? (1) Can the bunch shrink to microscopic dimensions ? No ! , Why not ? For the horizontal emittance h there is heating term due to the horizontal dispersion. What would stop dE and v of damping to zero? For v there is no heating term. So v can get very small. Coupling with motion in the horizontal plane finally limits the vertical beam size R. Steerenberg, 13-Jan-2011 AXEL - 2011 21 Is there a limit to this damping ? (2) In the transverse plane the damping seems to be limited. What about the longitudinal plane ? Whenever a photon is emitted the particle energy changes. This leads to small changes in the synchrotron oscillations. This is a random process. Adding many such random changes (quantum fluctuations), causes the amplitude of the synchrotron oscillation to grow. When growth rate = damping rate then damping stops, which give a finite equilibrium energy spread. R. Steerenberg, 13-Jan-2011 AXEL - 2011 22 Quantum fluctuations (1) Quantum fluctuation is defined as: Fluctuation in number of photons emitted in one damping time Let Ep be the average energy of one emitted photon Revolution time ET E seconds turns Damping time u u Energy loss/turn u Number of photons emitted/turn = E Number of emitted photons in one damping time can then be given by: R. Steerenberg, 13-Jan-2011 AXEL - 2011 p u E E Ep u Ep 23 Quantum fluctuations (2) E Number of emitted photons in one damping time = E Random E process r.m.s. deviation = E Energy of one emitted photon E E EE The r.m.s. energy deviation = E p p p p p The average photon energy Ep E3 The r.m.s. energy spread E2 The damping time E3 Higher energy faster longitudinal damping, but also larger energy spread R. Steerenberg, 13-Jan-2011 AXEL - 2011 24 Wigglers (1) The damping time in all planes ET u If the loss of energy, u, increases, the damping time decreases and the beam size reduces. To be able to control the beam size we add ‘wigglers’ N S N S N S N S N S N S beam S N S N S N S N S N S N It is like adding extra dipoles, however the wiggles does not give an overall trajectory change, but increases the photon emission R. Steerenberg, 13-Jan-2011 AXEL - 2011 25 Wigglers (2) What does the wiggler in the different planes? Vertically: We do not really need it (no heating term), but the vertical emittance would be reduced Horizontally: The emittance will reduce. A change in energy gives a change in radial position We know the dispersion function: dr D( s ) dE E In order to reduce the excitation of horizontal oscillations we should put our wiggler in a dispersion free area (D(s)=0) R. Steerenberg, 13-Jan-2011 AXEL - 2011 26 Wigglers (3) Longitudinally: The wiggler will increase the number of photons emitted It will increase the quantum fluctuations It will increase the energy spread Conclusion: Wigglers increase longitudinal emittance and decrease transverse emittance R. Steerenberg, 13-Jan-2011 AXEL - 2011 27 Summary Damping due to addition of longitudinal momentum ! Longitudinal: 4 Energy loss per turn: u Damping time: Transverse: 1 CE ET 4u rev 1 2ETrev Vertical damping time: u Horizontal damping time: 1 2 ET 1 u 1 2 R. Steerenberg, 13-Jan-2011 AXEL - 2011 28 Questions….,Remarks…? Synchrotron radiation Damping Quantum fluctuations Wigglers R. Steerenberg, 13-Jan-2011 AXEL - 2011 29