* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Electric Field Strength
History of electromagnetic theory wikipedia , lookup
Circular dichroism wikipedia , lookup
History of quantum field theory wikipedia , lookup
Electric charge wikipedia , lookup
Superconductivity wikipedia , lookup
Time in physics wikipedia , lookup
Electromagnet wikipedia , lookup
Maxwell's equations wikipedia , lookup
Lorentz force wikipedia , lookup
Mathematical formulation of the Standard Model wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
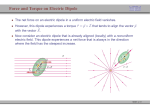
David A. Hill, et. al.. "Electric Field Strength." Copyright 2000 CRC Press LLC. <http://www.engnetbase.com>. Electric Field Strength1 47.1 Electrostatic Fields Field Mills • Calibration Field David A. Hill National Institute of Standards and Technology Motohisa Kanda National Institute of Standards and Technology 47.2 ELF and ULF Electric Fields Natural Horizontal Electric Field at the Earth’s Surface • FreeBody Electric Field Meters 47.3 Radio-Frequency and Microwave Techniques 47.4 47.5 Three-Loop Antenna System Broadband Dipole Antennas Dipole Antennas • Aperture Antennas Electric field strength is defined as the ratio of the force on a positive test charge at rest to the magnitude of the test charge in the limit as the magnitude of the test charge approaches zero. The units of electric field strength are volts per meter (V m–1). Electric charges and currents are sources of electric and magnetic fields, and Maxwell’s equations [1] provide the mathematical relationships between electromagnetic (EM) fields and sources. The electric field at a point in space is a vector defined by components along three orthogonal axes. → For example, in a rectangular coordinate system, the electric field E can be written as: r ˆ x + yE ˆ y + zE ˆ z E = xE (47.1) where xˆ, yˆ, and zˆ are unit vectors and Ex, Ey , and Ez are scalar components. For electrostatic fields, the components are real scalars that are independent of time. For steady-state, time-harmonic fields, the components are complex phasors that represent magnitude and phase. The time dependence, e jωt, is suppressed. 47.1 Electrostatic Fields Electrostatic fields are present throughout the atmosphere, and there are strong electrostatic fields near high-voltage dc power lines. The commonly used electrostatic field meters generate an ac signal by periodic conductor motion (either rotation or vibration). This ac signal is proportional to the electric field strength, and field meter calibration is performed in a known electrostatic field. 1 Contribution of the National Institute of Standards and Technology, not subject to copyright in the United States. © 1999 by CRC Press LLC FIGURE 47.1 Shutter-type electric field mill for measurement of the polarity and magnitude of an electrostatic field. Field Mills Field mills (also called generating voltmeters) determine electric field strength by measuring modulated, capacitively induced charges or currents on metal electrodes. Two types of field mills — the shutter type and the cylindrical type — are described in the technical literature [2]. The shutter type is more common; a simplified version is shown in Figure 47.1. The sensing electrode is periodically exposed to and shielded from the electric field by a grounded, rotating shutter. The charge qs induced on the sensing electrode and the current is between the sensing electrode and ground are both proportional to the electric field strength E normal to the electrode: () () qs t = e 0E as t () and is t = e 0E () da s t dt (47.2) where e0 is the permittivity of free space [1] and as(t) is the effective exposed area of the sensing electrode at time t. Thus, the field strength can be determined by measuring the induced charge or current (or voltage across the impedance Z). If the induced signal is rectified by a phase-sensitive detector (relative to the shutter motion), the dc output signal will indicate both the polarity and magnitude of the electric field [3]. © 1999 by CRC Press LLC FIGURE 47.2 Cylindrical field mill for measurement of electrostatic field strength. Shutter-type field mills are typically operated at the ground or at a ground plane, but a cylindrical field mill can be used to measure the electric field at points removed from a ground plane. A cylindrical field mill consists of two half-cylinder sensing electrodes as shown in Figure 47.2. Charges induced on the two sensing electrodes are varied periodically by rotating the sensing electrodes about the cylinder axis at a constant angular frequency ωc . The charge qc induced on a half- cylinder of length L and the current ic between the half-cylinders are given by: qc = 4 e 0rc LE sin ω ct and ic = 4 e0rc LE ω c cos ω ct (47.3) where rc is the cylinder radius. Equation 47.3 is based on the two-dimensional solution for a conducting cylinder in an electric field and neglects end effects for finite L. Equation 47.3 shows that the electric field strength E can be determined from a measurement of the induced charge or current. A third type of electric field meter uses a vibrating plate [4] to generate an ac signal that is proportional to the electric field strength. With any type of electric field strength meter, the observer should be at a sufficient distance from the measurement location to avoid perturbing the electric field. Calibration Field A known uniform field for meter calibration can be produced between a pair of parallel plates [2]. If a potential difference V is applied between a pair of plates with a separation dp , the field strength away from the plate edges is V/dp . The plate dimensions should be much larger than dp to provide an adequate region of uniform field. Also, dp should be much larger than the field meter dimensions so that the charge distribution on the plates is not disturbed. The parallel plates can be metal sheets or tightly stretched metal screens. The field meter should be located in the type of environment in which it will be used. Shutter-type field mills that are intended to be located at a ground plane should be located at one of the plates. Cylindrical field mills that are not intended to be used at a ground plane should be located in the center of the region between the plates. For simplicity, only field mills and calibration in the absence of space charge were mentioned. However, near power lines or in the upper atmosphere [5], the effects of space charge can be significant and require modifications in field mill design. A field mill for use in a space charge region and a calibration system with space charge are described in [6]. © 1999 by CRC Press LLC FIGURE 47.3 Grounded horizontal antenna for measurement of the horizontal component of the electric field. 47.2 ELF and ULF Electric Fields In this section, measurement techniques for extremely low frequency (ELF, 3 Hz to 3 kHz) and ultralow frequency (ULF, below 3 Hz) electric fields are considered. Natural ELF fields are produced by thunderstorms, and natural ULF fields are produced by micropulsations in the earth’s magnetic field [7]. Geophysicists make use of these natural fields in the magnetotelluric method for remote sensing of the Earth’s crust [8]. ac power lines are dominant sources of fields at 50 Hz or 60 Hz and their harmonics. An ac electric field strength meter [9] includes two essential parts: (1) an antenna and (2) a detector (receiver). Other possible features are a transmission line or optical link, frequency-selective circuits, amplifying and attenuating circuits, an indicating device, and a nonconducting handle. The antenna characteristics can be calculated for simple geometries or determined by calibration. For example, linear antennas are often characterized by their effective length Leff [10], which determines the open-circuit voltage Voc induced at the antenna terminals: Voc = Leff Einc (47.4) where Einc is the component of the incident electric field parallel to the axis of the linear antenna. The detector could respond to the terminal voltage or current or to the power delivered to the load. Natural Horizontal Electric Field at the Earth’s Surface Magnetotelluric sounding of the Earth’s crust requires measurement of the horizontal electric and magnetic fields at the Earth’s surface [8]. The magnetic field is measured with a horizontal axis loop, and the electric field is measured with a horizontal wire antenna as shown in Figure 47.3. The antenna wire is insulated since it lies on the ground, but it is grounded at its end points. Nonpolarizing grounding electrodes should be used to avoid polarization potentials between the electrodes and the ground. Since the natural electric field strength to be measured is on the order of 1 µV m–1, the antenna length Lh needs to be on the order of 1 km to produce a measurable voltage. Since the effective length of a grounded antenna is equal to the physical length (Leff = Lh), the horizontal component Eh of the electric field parallel to the antenna is equal to the open-circuit voltage divided by the antenna length: E h = Voc Lh (47.5) The frequencies used in typical magnetotelluric sounding range from approximately 0.1 mHz to 10 Hz. If both horizontal components of the electric field are needed, a second orthogonal antenna is required. © 1999 by CRC Press LLC FIGURE 47.4 Electric field meters for measurement of the axial component of the electric field: (a) spherical geometry and (b) rectangular geometry. Free-Body Electric Field Meters ELF electric fields in residential and industrial settings are most conveniently measured with free-body field meters [11, 12], which measure the steady-state current or charge oscillating between two halves of a conducting body in free space. (Ground reference meters [13] are also available for measuring the electric field normal to the ground or some other conducting surface.) Geometries for free-body electric field meters are shown in Figure 47.4. Commercial field meters are usually rectangular in shape, and typical dimensions are on the order of 10 cm. A large dynamic range (1 V m–1 to 30 kV m–1) is required to cover the various field sources (ac power lines, video display terminals, mass transportation systems, etc.) of interest. (Electro-optic field meters with less sensitivity are described in [12].) A long, nonconducting handle is normally attached perpendicular to the field-meter axis for use in measurement surveys. The charge Q on half of the field meter is proportional to the incident electric field E along the meter axis: Q = A e0E (47.6) where e0 is the permittivity of free space [1] and A is a constant proportional to the surface area. For the spherical geometry in Figure 47.4(a), A = 3πa2, where a is the sphere’s radius. Since the current I between the two halves is equal to the time derivative of the charge, for time-harmonic fields it can be written: I = jωA e 0E (47.7) This allows E to be determined from the measured current. For commercial field meters that are not spherical, the constant A needs to be determined by calibration. A known calibration field can be generated between a pair of parallel plates where the plates are sufficiently large compared to the separation to produce a uniform field with small edge effects. This technique produces a well-characterized field with an uncertainty less than 0.5% [11]. However, the presence of harmonic frequencies can cause less accurate meter readings in field surveys. 47.3 Radio-Frequency and Microwave Techniques Dipole Antennas A thin, linear dipole antenna of length L is shown in Figure 47.5. Its effective length is approximately [10]: © 1999 by CRC Press LLC FIGURE 47.5 Dipole antenna for measurement of the axial component of the electric field. Leff = πL λ tan π 2λ (47.8) where λ is the free-space wavelength. Resonant half-wave dipoles (L = λ/2) have an effective length of Leff = 2L/π and are of convenient length for frequencies from 30 to 1000 MHz. The physical length of a dipole at resonance is actually slightly shorter than λ/2 to account for the effect of a finite length-todiameter ratio. Resonant dipoles are used as standard receiving antennas to establish a known standard field in the standard antenna method [9]. Commercial antennas and field meters are calibrated in such standard fields. For L < λ/2, Equation 47.8 must be used to determine Leff. For very short dipoles (L/λ << 1), the current distribution is approximately linear, and the effective length is approximately one half the physical length (Leff ≈ L/2). Short dipoles are frequently used as electric field probes. Aperture Antennas Aperture antennas are commonly used for receiving and transmitting at microwave frequencies (above 1 GHz). As receiving antennas, they are conveniently characterized by their on-axis gain g or effective area Aeff . Effective area is defined as the ratio of the received power Pr to the incident power density Sinc and can also be written in terms of the gain [9]: Aeff = Pr gλ2 = Sinc 4 π (47.9) Equation 47.9 applies to the case where the incident field is polarization-matched to the receiving antenna. The incident power density in a plane wave is Sinc = E2/η0, where E is the rms electric field strength and η0 is the impedance of free space (≈377 Ω). Thus, the electric field strength can be determined from the received power: E = Pr η0 Aeff = λ−1 4 πη0 Pr g (47.10) In general, the gain can be measured using the two-antenna method [9]. For a pyramidal horn antenna as shown in Figure 47.6, the gain can be calculated accurately from [14]: g= © 1999 by CRC Press LLC 32 ab πλ2 RE RH (47.11) FIGURE 47.6 Pyramidal horn for measuring power density or electric field strength. where RE and RH are gain reduction factors due to the E and H plane flare of the horn. The gain reduction factors are RE = Where: () () C2 w + S2 w w2 w= [ ( ) ( )] [ ( ) ( )] 2 π2 C u − C v + S u − S v and RH = 2 4 u−v ( ) b 2λlE and λlH 2 u ± = a v 2 , (47.12) a 2λlH The Fresnel integrals C and S are defined as [15]: w w π π C w = cos t 2 dt and S w = sin t 2 dt 2 2 () ∫ 0 () ∫ (47.13) 0 Well-characterized aperture antennas are also used to generate standard fields [16] for calibrating commercial antennas and field strength meters. This method of calibration is called the standard field method [9]. The electric field strength E at a distance d from the transmitting antenna is: ( ) E = η0 Pdel g 4 π © 1999 by CRC Press LLC d, (47.14) FIGURE 47.7 Geometry of the three-loop antenna system and the device under test. where Pdel is the net power delivered to the transmitting antenna and is typically measured with a directional coupler [16]. The gain g for a pyramidal horn can be calculated from Equation 47.11. The National Institute of Standards and Technology (NIST) uses rectangular open-ended waveguides from 200 MHz to 500 MHz and a series of pyramidal horns from 500 MHz to 40 GHz to generate standard fields in an anechoic chamber [16]. The uncertainty of the field strength is less than 1 dB over the entire frequency range of 200 MHz to 40 GHz. 47.4 Three-Loop Antenna System Electronic equipment can emit unintentional electromagnetic radiation that can interfere with other electronic equipment. If the radiating source is electrically small (as is a video display terminal), then it can be characterized by equivalent electric and magnetic dipole moments. The three-loop antenna system (TLAS), shown in Figure 47.7, consists of three orthogonal loop antennas that are terminated at diametrically opposite points. The unique feature of loop antennas with double terminations [17] is that they can measure both electric and magnetic fields. For electromagnetic interference (EMI) applications, a device under test (DUT) is placed at the center of the TLAS. On the basis of six terminal measurements, the TLAS determines three equivalent electric dipole components and three equivalent magnetic dipole moments of the DUT and hence its radiation characteristics. Here, the theory [18] is summarized for one of the three loops. The DUT in Figure 47.7 is replaced → → by an electric dipole moment me and a magnetic dipole moment mm, both located at the origin of the coordinate system. The dipole moments can be written in terms of their rectangular components: r r ˆ ex + ym ˆ ey + zm ˆ ez and mm = xm ˆ mx + ym ˆ my + zm ˆ mz me = xm (47.15) The loop in the xy plane has radius r0 and has impedance loads Zxy located at the intersections with the x axis (φ = 0, π). The solution for the current induced in the loop is based on Fourier series analysis [19]. The incident azimuthal electric field Eφi(φ) tangent to the loop is: © 1999 by CRC Press LLC () Eφi φ = A0 + A1 cos φ + B1 sin φ (47.16) A0 = mmxGm Where: A1 = meyGe B1 = −mexGe Gm = η0 k 2 jk − jkr0 − e 4 π r0 r02 Ge = − η0 jk 1 1 − jkr0 + 2+ e 4 π r0 r0 jkr02 and k = 2π/λ is the free-space wavenumber. An approximate solution [17] for the loop current I(φ) yields the following results for the load currents I(0) and I(π): m G Y meyGeY1 I 0 = 2πr0 mz m 0 + 1 + 2Y0 Z xy 1 + 2Y1Z xy () (47.17) m G Y m GY I π = 2πr0 mz m 0 − ey e 1 1 + 2Y0 Z xy 1 + Y1Z xy () where Y0 and Y1 are the admittances for the constant and cosφ currents [17]. One can solve Equation 47.17 for the magnetic and electric dipole components: mmz = ( I Σ 1 + 2Y0 Z xy 2πr0GmY0 ) and m ey = ( I ∆ 1 + 2Y1Z xy 2πr0GeY1 ) (47.18) [ ( ) ( )] 2 = [ I (0) − I ( π)] 2 IΣ = I 0 + I π Where: I∆ Thus, the sum current IΣ can be used to measure the magnetic dipole moment, and the difference current I∆ can be used to measure the electric dipole moment. The four remaining dipole components can be obtained in an analogous manner. The loop in the xz plane can be used to measure mmy and mex , and the loop in the yz plane can be used to measure mmx and mez . The total power PT radiated by the source can be written in terms of the magnitudes of the six dipole components: PT = 2 2 2 2 2 2 2πη0 m + mey + mez + k 2 mmx + mmy + mmz 2 ex 3λ (47.19) The expression for the power pattern is more complicated and involves the amplitudes and phases of the dipole moments [20]. The TLAS has been constructed with 1-m diameter loops and successfully © 1999 by CRC Press LLC tested from 3 kHz to 100 MHz [21]. It is currently being used to measure radiation from video display terminals and other inadvertent radiators. 47.5 Broadband Dipole Antennas The EM environment continues to grow more severe and more complex as the number of radiating sources increases. Broadband antennas are used to characterize the EM environment over a wide frequency range. For electric-field measurements, electrically short dipole antennas with a high capacitive input impedance are used with a capacitive load, such as a field-effect transistor (FET). The transfer function S of frequency f is defined as the ratio of the output voltage VL of the antenna to the incident electric field Ei [22]: () S f = ( ) = hα 2 E ( f ) 1+ C C VL f Ca = Where: α= ( 4 πh cη0 Ωa − 2 − ln 4 ) Ωa − 1 Ωa − 2 + ln 4 ( Ωa = 2 ln 2 h ra ra C Ca h c Ωa (47.20) a i ) = Antenna radius = Load capacitance = Antenna capacitance = Half the physical length of the dipole antenna, as shown in Figure 47.5 = Free-space speed of light = Antenna thickness factor Since the input impedance of an electrically short dipole is predominantly a capacitive reactance, a very broadband frequency response can be achieved with a high-impedance capacitive load. However, given the present state of the art, it is not possible to build a balanced, high-input impedance FET with high common-mode rejection above 400 MHz. For this reason, it is more common practice to use a high-frequency, beam-lead Schottky-barrier diode with a very small junction capacitance (less than 0.1 pF) and very high junction resistance (greater than several M3) for frequencies above 400 MHz. The relationship between the time-dependent diode current id(t) and voltage vd(t) is () α v t id t = I s e d d ( ) − 1 (47.21) where Is and αd are constants of the diode. For very small incident fields Ei(t), the output detected dc voltage v0 is: v0 = © 1999 by CRC Press LLC −bd2 2 v˜i 2 αd (47.22) vi = Ei Le () () v˜i t = vi t − vi Where: bd = Ca α d Ca + Cd Ca = Dipole capacitance Cd = Diode capacitance Le = Effective length of the dipole antenna < > Indicates time average Thus, the dc detected voltage is frequency independent and is directly proportional to the average of (Ei – <Ei >)2. For large incident fields Ei(t), the output detected dc voltage is: v0 = − bdV˜i αd (47.23) where Ṽi is the peak value of vi(t). Consequently, for a large incident field, v0 is also frequency independent and is directly proportional to the peak field. Conventional dipole antennas support a standing-wave current distribution; thus, the useful frequency range of this kind of dipole is usually limited by its natural resonant frequency. In order to suppress this resonance, a resistively loaded dipole (traveling-wave dipole) has been developed. If the internal impedance per unit length Zl(z) as function of the axial coordinate z (measured from the center of the dipole) has the form: () Zl z = 60 ψ (47.24) h− z then the current distribution Iz(z) along the dipole is that of a traveling wave. Its form is () Iz z = z 1 − e − jk z 60 ψ 1 − j kh h V0 ( ) (47.25) where 2h = Total physical length of the dipole V0 = Driving voltage h ψ = 2 sinh −1 − C 2 kad , 2 kh − jS 2 kad , 2 kh ad ( ) ( ) + khj (1 − e ) − j 2 kh (47.26) C(x,y) and S(x,y) = Generalized cosine and sine integrals = Dipole radius ad This type of resistively tapered dipole has a fairly flat frequency response from 100 kHz to 18 GHz [23]. © 1999 by CRC Press LLC Defining Terms Electric field strength: The ratio of the force on a positive test charge to the magnitude of the test charge in the limit as the magnitude of the test charge approaches zero. Electrostatic field: An electric field that does not vary with time. Field mill: A device used to measure an electrostatic field. Antenna: A device designed to radiate or to receive time-varying electromagnetic waves. Microwaves: Electromagnetic waves at frequencies above 1 GHz. Power density: The time average of the Poynting vector. Aperture antenna: An antenna that radiates or receives electromagnetic waves through an open area. Dipole antenna: A straight wire antenna with a center feed used for reception or radiation of electromagnetic waves. References 1. J.A. Stratton, Electromagnetic Theory, New York: McGraw-Hill, 1941. 2. ANSI/IEEE Std. 1227-1990, IEEE Guide for the Measurement of DC Electric-Field Strength and Ion Related Quantities. 3. P.E. Secker and J.N. Chubb, Instrumentation for electrostatic measurements, J. Electrostatics, 16, 1–19, 1984. 4. R.E. Vosteen, DC electrostatic voltmeters and fieldmeters, Conference Record of Ninth Annual Meeting of the IEEE Industrial Applications Society, October 1974. 5. P.J.L. Wildman, A device for measuring electric field in the presence of ionisation, J. Atmos. Terr. Phys., 27, 416–423, 1965. 6. M. Misakian, Generation and measurement of dc electric fields with space charge, J. Appl. Phys., 52, 3135–3144, 1981. 7. G.V. Keller and F.C. Frischknecht, Electrical Methods in Geophysical Prospecting, Oxford, U.K.: Pergamon Press, 1966. 8. A.A. Kaufman and G.V. Keller, The Magnetotelluric Sounding Method, Amsterdam: Elsevier, 1981. 9. IEEE Std. 291-1991, IEEE Standard Methods for Measuring Electromagnetic Field Strength of Sinusoidal Continuous Waves, 30 Hz to 30 GHz. 10. E.C. Jordan and K.G. Balmain, Electromagnetic Waves and Radiating Systems, 2nd ed., Englewood Cliffs, NJ: Prentice-Hall, 1968. 11. ANSI/IEEE Std. 644-1987, IEEE Standard Procedures for Measurement of Power Frequency Electric and Magnetic Fields from AC Power Lines. 12. IEEE Std. 1308-1994, IEEE Recommended Practice for Instrumentation: Specifications for Magnetic Flux Density and Electric Field Strength Meters — 10 Hz to 3 kHz. 13. C.J. Miller, The measurements of electric fields in live line working, IEEE Trans. Power Apparatus Sys., PAS-16, 493–498, 1967. 14. E.V. Jull, Aperture Antennas and Diffraction Theory, Stevenage, U.K.: Peter Peregrinus, 1981. 15. M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions, Nat. Bur. Stand. (U.S.), Spec. Pub. AMS 55, 1968. 16. D.A. Hill, M. Kanda, E.B. Larsen, G.H. Koepke, and R.D. Orr, Generating standard reference electromagnetic fields in the NIST anechoic chamber, 0.2 to 40 GHz, Natl. Inst. Stand. Technol. Tech. Note 1335, 1990. 17. M. Kanda, An electromagnetic near-field sensor for simultaneous electric and magnetic-field measurements, IEEE Trans. Electromag. Compat., EMC-26, 102–110, 1984. 18. M. Kanda and D.A. Hill, A three-loop method for determining the radiation characteristics of an electrically small source, IEEE Trans. Electromag. Compat., 34, 1–3, 1992. 19. T.T. Wu, Theory of the thin circular antenna, J. Math. Phys., 3, 1301–1304, 1962. © 1999 by CRC Press LLC 20. I. Sreenivasiah, D.C. Chang, and M.T. Ma, Emission characteristics of electrically small radiating sources from tests inside a TEM cell, IEEE Trans. Electromag. Compat., EMC-23, 113–121, 1981. 21. D.R. Novotny, K.D. Masterson, and M. Kanda, An optically linked three-loop antenna system for determining the radiation characteristics of an electrically small source, IEEE Int. EMC Symp., 1993, 300–305. 22. M. Kanda, Standard probes for electromagnetic field measurements, IEEE Trans. Antennas Propagat., 41, 1349–1364, 1993. 23. M. Kanda and L.D. Driver, An isotropic electric-field probe with tapered resistive dipoles for broadband use, 100 kHz to 18 GHz, IEEE Trans. Microwave Theory Techniques, MTT-35, 124–130, 1987. © 1999 by CRC Press LLC