* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Thevenin & Norton Equivalent
Electrical substation wikipedia , lookup
Stepper motor wikipedia , lookup
History of electric power transmission wikipedia , lookup
Voltage regulator wikipedia , lookup
Schmitt trigger wikipedia , lookup
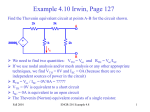
Switched-mode power supply wikipedia , lookup
Voltage optimisation wikipedia , lookup
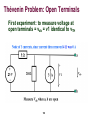
Electrical ballast wikipedia , lookup
Surge protector wikipedia , lookup
Stray voltage wikipedia , lookup
Buck converter wikipedia , lookup
Two-port network wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Mains electricity wikipedia , lookup
Opto-isolator wikipedia , lookup
Alternating current wikipedia , lookup
Rectiverter wikipedia , lookup
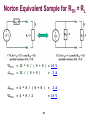
ECE 221 Electric Circuit Analysis I Chapter 13 Thévenin & Norton Equivalent Herbert G. Mayer, PSU Status 11/3/2015 1 Syllabus Motivation Thought Experiment Purpose Thévenin Problem Norton Equivalent A Sample Thévenin vs. Source Transformations Thévenin With Dependent Sources Exercise 1 References 2 Motivation When working with real electric sources, such as typical household power supplies, the actual circuit behind the terminals is unknown It should be unknown! Unreasonable to expect users to know what exactly is behind the electric terminal! We only know 1.) that there is a source of constant voltage at terminals a and b with a complex but finite resistance internally And 2.) that the current supplied depends on external load, up to some practical limits When the limit is exceeded, a fuse flips and we lose power 3 Motivation It is desirable to understand the physical limits of such a CVS Once we know the limits, we can model the whole complex CVS source with an equivalent, but simpler alternative One such model is the Thévenin equivalent, an imaginary CVS with identical behavior Named after 19th century French telegraph engineer Léon Charles Thévenin, 1857-1926 Such a Thévenin equivalent source consists of CVS with vTh Volt and an internal resistance of RTh Ω in series; and nothing else! 4 Thought Experiment We only know 1.) that the black (green) box contains constant voltage- and current sources; 2.) its voltage at the terminals; 3.) that the current is finite, limited by some practical maximum How to model this situation? Answered by the Thévenin Equivalent 5 Thought Experiment We find the Thévenin parameters, modeling the green box, by practicing the following experiments: 1. Leaving the circuit open at terminals a and b, allows measuring the voltage vTh with no load, i.e. load with resistance RL = ∞ Measuring the voltage yields vTh 2. Short-circuiting the terminals a and b allows us to measure the maximum load current iSC Measuring that short-circuit current yields iSC 3. Thus we can compute RTh RTh = vTh / iSC 6 Conclusion: Thévenin Equivalent A Thévenin Equivalent circuit is a simple, CVS circuit with a serial resistor, RTH . . . . . . electrically equivalent to an arbitrary linear circuit, whose key parameters, idle voltage and short-circuit current are measurable Such a circuit’s equivalent resistance is: RTh = vTh / iSC A sample Thévenin transformation follows, taken from [1], p. 113-115 7 Sample Thévenin Problem Looking at the terminals (a) and (b) from the right, we pretend not to know what’s behind them; only that vab is delivered. Measure 2 key parameters; in the end replace what’s there with the Thévenin equivalent: 8 Sample Thévenin Problem The following circuit has various internal sources and resistances, 2 external terminals (a) and (b) Goal is to model the exact behavior of this circuit via the RTh and iSC equivalents First measure idle voltage VTh at the terminals, here called vab, then measure the short-circuit current iSC Thus we can compute the resulting equivalent resistance RTh: RTh = vTh / iSC With terminals open, no current flows in 4 Ω resistor We compute v1, parallel to the CCV and the 20 Ω resistor Note: with open terminals, the 4 Ω resistor in this circuit might as well be missing! The voltage drop along the 4 Ω resistor is 0 V 9 Thévenin Problem: Open Terminals First experiment: to measure voltage at open terminals = vab = v1 identical to vTH 10 Thévenin Problem: Open Terminals (v1 - 25)/5 + v1/20 - 3 = 0 Students compute v1 = vTH! 11 Thévenin Problem: Open Terminals (v1 - 25)/5 + v1/20 - 3 = 0 4*v1 -100 -60 + v1 = 0 5*v1 = 160 v1 = vab = vTh = 32 V vTh = 32 V 12 Thévenin Problem: Short-Circuit In the next experiment terminals (a) and (b) are short-circuited A real current flows through the 4 Ω R, now parallel to the 3 A CCS We compute v2, the voltage along the 3 A CCS, using the NoVoMo Once v2 is known, then all other units, specifically iSC can be computed 13 Sample Thévenin Problem 14 Thévenin Problem: Short-Circuit v2/20 + (v2-25)/5 - 3 + v2/4 Students Compute v2 15 = 0 Thévenin Problem: Short-Circuit v2/20 + (v2-25)/5 - 3 + v2/4 = 0 v2 + 4*v2 + 5*v2 = 160 10*v2 = 160 v2 = 16 V vTH = 32 V iSC = v2/4 = 16/4 = 4 A RTh = vTh/iSC = 32/4 = 8 Ω 16 Final Thévenin Equivalent Circuit 17 Short-Cut For Thévenin Resistance A simpler way to compute the Thévenin Equivalence resistance for a linear circuit with only CCS, CVS, and resistances --does not work with dependent sources!: Open all CCS, and short-circuit all CVS, compute the resulting resistance REQ which is the final RTH 18 Short-Cut For Thévenin Resistance All CCS are left open, all CVS are short-circuited, resulting equivalent R = 8 Ω 20 Ω and 5 Ω in parallel = 4 Ω, plus 4 Ω in series = 8 Ω 19 Norton Equivalent Method 1: Earlier we covered transforming some CVS into an equivalent CCS Method 2: The Thévenin transformation, introduced here, yields a CVS with R in series We can combine the 2 methods and generate a CCS equivalent to any CVS-circuit by just measuring idle voltage and short-circuit current The equivalent Norton current iN is 4 A, with the 8 Ω resistor in parallel: iN = iTh = 32/8 = 4 A iN = 4 A 20 Norton Equivalent Sample for RTH = RL VLCVS = 32 * 8 / ( 8 + 8 ) = 16 V iLCVS = 32 / ( 8 + 8 ) = 2 A iLCCS = 4 * 8 / ( 8 + 8 ) = 2 A VLCCS = 4 * 8 / 2 = 16 V 21 Thévenin- vs. Source Transformation Instead of using Thévenin equivalent, use successive source-tosource transformations to reduce a complex circuit into one as simple as Thévenin equivalent. What will it look like? Transformation 1: starting on the left side, substitute 25 V CVS with R in series into equivalent CCS with R in parallel: 22 Thévenin- vs. Source Transformation Students, transform 25 V CVS with 5 Ohm in series into equivalent CCS with 5 Ohm in parallel 23 Source Transformation 1 Transformation 1: as a result, we have 2 resistors or 5 Ohm and 20 Ohm and 2 CCS in parallel; can be combined trivially 24 Source Transformation 2 Combined 20 Ω and 5 Ω into an equivalent 4 Ω. Combined 5 A and parallel 3 A CCS into an equivalent 8 A CCS. Now convert back into CVS: 25 Source Transformation 3 As a result, we have two 4 Ω resistors in series. Trivial transformation. See next simple replacement! 26 Source Transformation 4 Simple transformation, two 4 Ω become one 8 Ω Now convert CVS back into equivalent CCS Happens to be Thévenin Equivalent 27 Source Transformation 4 Students, transform 32 V CVS and 8 Ohm in series into equivalent CCS with 8 Ohm in parallel 28 Source Transformation 5 Final transformation shows that Thévenin equivalent at terminals (a) and (b) is the same as source-to-source transformation down to minimal number of components! Thévenin equivalent is: vTH = 32 V, iSC = 4 A, and RTH = 8 Ω With CCS, happens to be the Norton Equivalent 29 Thévenin Equivalent With Dependent Sources (Taken from [1]) 30 Find Thévenin: Dependent Sources Consider circuit C1 below: what is the Thévenin Equivalent at terminals (a) and (b)? Can it be simplified by totally omitting the left part, since ix = 0 ? To answer that we exercise the Thévenin transformation: open terminals and short-circuited terminals (a) and (b) 31 Find Thévenin: Dependent Sources Can circuit C1 be simplified by omitting left part, since ix = 0 A? Clearly not! See C2, which is NOT an equivalent option, since both parts, left and right, depend on electric units of their mutual other half The dependent current source is a function of i namely 20 * i, flowing through the 2 kΩ resistor on the left part And the dependent voltage source is a function of voltage vab along the 25 Ω resistor, namely 3*v = 3*vab 32 Find Thévenin: Dependent Sources Is C3 equivalent to C1? Yes, since ix = 0 A, but circuit analysis needs both parts due to mutual dependencies Goal to find Thévenin Equivalent of circuit C1 Step 1: Compute v = vab = vTH of C1 with terminals (a) and (b) open Step 2: Compute current iSC with terminals (a) and (b) shortcircuited 33 Thévenin Equivalent Step 1 Step 1: Compute v = vab = vTH of C1 with terminals (a) and (b) open: i = ( 5 – 3 * v ) / 2000 = ( 5 – 3 * vTH ) / 2000 34 Thévenin Equivalent Step 1 Step 1: Compute v = vab = vTH of C1 with terminals (a) and (b) open: i = ( 5 – 3 * v ) / 2000 AKA i v = -20 * 25 * i AKA vTH = -500 * i = ( 5 – 3 * vTH ) / 2000 Students, compute v = vTH 35 Thévenin Equivalent Step 1 Step 1: Compute v = vab = vTH of C1 with terminals (a) and (b) open: i = ( 5 – 3 * v ) / 2000 AKA i v = -20 * 25 * i AKA vTH = -500 * i = ( 5 – 3 * vTH ) / 2000 vTH = -500 * ( 5 – 3 * vTH ) / 2000= -5 * ( 5 – 3 * vTH ) / 20 vTH = -25 / 20 + vTH * 15 / 20 -- multiply by * 20 20 * vTH = -25 + vTH * 15 5 * vTH = -25 vTH = -5 V 36 Thévenin Equivalent Step 2 Step 2: Compute i = iSC with terminals (a) and (b) short-circuited Short-circuit bypasses 25 Ω resistor; that means the voltage controlling the dependent voltage source is also shortcircuited, i.e. the voltage drop is 0 V. That dependent source can be removed. Note that the 20 * i and iSC run in opposite directions! Sign!! 37 Thévenin Equivalent Step 2 Step 2: Compute i = iSC with terminals (a) and (b) short-circuited Note that the 20 * i and iSC run opposite directions! i = iSC = 5 / 2000 = 2.5 mA - 20 * i iSC = -50 mA With iSC RTH = -50 mA, vTH = -5 V we get = - 5 / -50 * 1000 [ V / A ] RTH = 1/10 k Ω = 100 Ω 38 Thévenin Equivalent With Dependent Below we have C5, the Thévenin Equivalent circuit of the original C1 circuit With dependent sources the convenient short-cut (p. 19 above) for computing RTH does not work! Note reversed polarity of 5 V CVS in C5! 39 Norton Equivalent of C1 The Norton Equivalent has the 100 Ω resistor parallel to the constant current source of 5 V / 100 Ω = 50 mA Note the direction of the CCS, the tip pointing to the + sign of the equivalent CVS! 40 Exercise 1 41 Exercise 1: Thévenin Equivalent Given the circuit below, generate the Thevénin equivalent First leave terminals (a) and (b) open and compute vTH Then short-circuit terminals (a) and (b), and compute iSC Yielding the Thevénin equivalent vTH, iSC, including resistance RTH 42 Exercise 1 Open: Thévenin Equivalent With open plugs, the voltage drop vTH at terminals (a) and (b) is the same as along the CCS with 4 A CCS pushes 4 A through 6 Ω resistor, creating 4 * 6 = 24 V voltage drop Ohms Law: yields 6 * 4 = 24 V: vTH = 24 + 12 = 36 V 43 Exercise 1 SC: Thévenin Equivalent With terminals (a) and (b) short-circuited, iSC runs through the 14 Ω resistor, and i6 through the 6 Ω resistor KCL: iSC – 4 + i6 = 0 KVL: 14 * iSC – 12 – 6 * i6 = 0 iSC 1.8 A RTH = = vTH / iSC = 44 36 / 1.8 = 20 Ω Exercise 1: Thévenin Equivalent VTH Easier to use the Node Voltage Methodology to compute iSC: KCL: v / 14 – 4 + ( v – 12 ) / 6 = 0 v = 14*36 / 20 iSC = v / 14 = 14 * 36 / ( 20 * 14 ) iSC = 36 / 20 = 1.8 A Yields iSC: RTH = vTH / iSC = 45 36 / 1.8 = 20 Ω Exercise 1: A Simpler Way To identify RTH, all we need to do is short-circuit all CVSs, eliminate all CCSs, and compute the equivalent REQ, which is RTH This just leaves the 2 resistors in series, resulting RTH = 20 Ω 46 Finally: Thévenin Equivalent The circuit below shows the equivalent Thévenin arrangement 47 References 1. Electric Circuits, James W. Nielsson and Susan A. Riedel, Pearson Education Inc., publishing as as Prentice Hall, © 2015, ISBN13: 978-0-13-376003-3 48