* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter 1 - UniMAP Portal
Index of electronics articles wikipedia , lookup
Galvanometer wikipedia , lookup
Integrating ADC wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Electrical ballast wikipedia , lookup
RLC circuit wikipedia , lookup
Power electronics wikipedia , lookup
Voltage regulator wikipedia , lookup
Power MOSFET wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current source wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
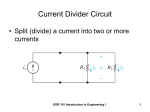
CHAPTER 1 BASIC ELECTRICAL CONCEPTS AND RESISTIVE CIRCUITS - Introduction to electric circuit - SI Unit, Electrical Unit - Electric Charge, Current, Voltage, Resistance and Power - Basic circuit elements : Active element and Passive element Continue… - Ohm’s Law - Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) - Series and Parallel circuit - Voltage Divider Rule (VDR) and Current Divider Rule (CDR) BASIC ELECTRICAL CONCEPTS AND RESISTIVE CIRCUITS - Introduction to electric circuit - SI Unit, Electrical Unit - Electric Charge, Current, Voltage, Resistance and Power - Basic circuit elements : Active element and Passive element Introduction to Electric Circuit Electric circuit can be defined as an interconnection between components or electrical devices for the purpose of communicating or transferring energy from one point to another. The components of electric circuit are always referred to as circuit elements. BASIC ELECTRICAL CONCEPTS AND RESISTIVE CIRCUITS - Introduction to electric circuit - SI Unit, Electrical Unit - Electric Charge, Current, Voltage, Resistance and Power - Basic circuit elements : Active element and Passive element • QUANTITY AND ELECTRICAL UNIT SI Unit SI : International System of Unit that had been introduced by National Bureau of Standards in 1964 Quantity Basic Units Symbol Length Meter m Mass Kilogram kg Time Second s Electric Current Ampere A Temperature Kelvin K Luminous intensity candela cd SI unit consists of decimal system that connected to the smaller or bigger of basic unit and by using prefix for the power of tenth: Multiplier Prefix Symbol 1018 Exa E 1015 Peta P 1012 Tera T 109 Giga G 106 Mega M 103 Kilo k 102 Hector h 101 Deka da 10-1 Deci d 10-2 Centi d 10-3 Mili m 10-6 Micro 10-9 Nano n 10-12 Pico p 10-15 Femto f 10-18 Atto a The derived unit commonly used in electric circuit theory BASIC ELECTRICAL CONCEPTS AND RESISTIVE CIRCUITS - Introduction to electric circuit - SI Unit, Electrical Unit - Electric Charge, Current, Voltage, Resistance and Power - Basic circuit elements : Active element and Passive element ELECTRIC CHARGE • • • • Polarity: type of charge (-ve or +ve) Electron: -ve charge Proton: +ve charge Electric charge create electric field of force Electric charge is an electrical property of the atomic particles of which matter consists measured in coulombs (C). Continued… The charge e on one electron is negative and equal in magnitude to 1.602 10-19 C which is called as electronic charge. The charges that occur in nature are integral multiples of the electronic charge. ELECTRIC CHARGE Quantity is Charge (Q) Base Unit is Coulomb (C) Examples of correct usage: Charge = 10 Coulombs Q = 10 C CURRENT Current is defined as the movement of charge in a specified direction. Electric Current Terminology Quantity is Current (I) Base Unit is Ampere (A) An Ampere = Coulomb per second Examples of usage: Current = 10 Amperes I = 10 A Electric Current Relationships Charge Current = Time Q I= t Electric current i = dq/dt. The unit of ampere can be derived as 1 A = 1C/s. Examples: Q 10 C = 2 A I= t = 5s TYPES OF CURRENT i t Direct current (arus terus) Alternating current (arus ulangalik) A direct current (dc) is a current that remains constant with time. An alternating current (ac) is a current that varies sinusoidally with time. (reverse direction) Example A conductor has a constant current of 5 A. How many electrons pass a fixed point on the conductor in one minute? Solution Total no. of charges pass in 1 min is given by 5 A = (5 C/s)(60 s/min) = 300 C/min Total no. of electronics pass in 1 min is given 300 C/min 21 1.87 x10 electrons/ min 19 1.602 x10 C/electron VOLTAGE • Voltage is the electric pressure or force that causes current. • It is a potential energy difference between two points. • It is also known as an electromotive force (emf). Voltage Terminology Quantity is Voltage (V) Base Unit is Volt (V) A Volt = Joule per second Examples of usage: Voltage = 20 Volts V = 20 V Voltage Relationships Voltage = Energy V= W Q Charge Examples: W V= Q = 24 J = 6 V 4C RESISTANCE Resistance is the opposition a material offers to current. Resistance is determined by: • Type of material (resistivity) • Temperature of material • Cross-sectional area • Length of material Resistance Terminology Quantity is Base Unit is RESISTANCE (R) OHM (W) An ohm = Volt per ampere Example of usage: Resistance = 14 ohm R = 14 Ω Resistance Relationships Resistivity x length KL Resistance = R= A area Example: 1.4 x10-6 W cm x 5 x104 cm KL = R= A 2 cm2 = 5W POWER Power is the rate of using energy or doing work. Energy (W) Work (W) consists of a force moving through a distance. is the capacity to do work. Joule (J) is the base unit for both energy and work. Power Terminology Quantity is POWER (P) Base Unit is WATT (W) A watt = Joule per second Example of usage: Power = 200 Watts P = 200 W Power Relationships Energy Power = Time W P= t Example: 200 J = 10 W W P = t = 20 s BASIC ELECTRICAL CONCEPTS AND RESISTIVE CIRCUITS - Introduction to electric circuit - SI Unit, Electrical Unit - Electric Charge, Current, Voltage, Resistance and Power - Basic circuit elements : Active element and Passive element ACTVIVE ELEMENT AND PASSIVE ELEMENT Active Element– elements capable of • • • • generating electrical energy. For example: Voltage source Current source Passive Element – elements are not capable of generating electrical energy. For example: Resistor (dissipates energy) Capacitor and Inductor (can store or release energy) Independent source This source maintains a specified voltage between its terminals but has no control on the current passing through it. The symbol of the independent voltage source is a plus-minus sign enclosed by a circle. Voltage Current This source maintains a specified current through its terminals but has no control on the voltage across its terminals. The symbol of the independent current source is an arrow enclosed by a circle. Voltage Dependent source Current Vs ix This kind of voltage source has a specified voltage between its terminals but it is dependable on some other variable defined somewhere in the circuit. The symbol for the dependent voltage source is a plus-minus sign enclosed by a diamond shape. The value of the dependent current source is ρix (ohms) where ρ is the scale factor or gain. is Vx This kind of current source has a specified current between its terminals but it is dependent on some other variable defined somewhere in the circuit. The symbol for the dependent current source is an arrow enclosed by a diamond shape. The value of the dependent current source is αVx (in Siemens) where α is the scale factor or gain. Example Obtain the voltage v in the branch shown in Figure below for i2 = 1A. Solution Voltage v is the sum of the currentindependent 10-V source and the current-dependent voltage source vx. Note that the factor 15 multiplying the control current carries the units Ω. Therefore, v = 10 + vx = 10 + 15(1) = 25 V Circuit symbol of resistor Resistor R UNIT: Ohm (Ω) Resistor is passive element that dissipates electrical energy. Linear resistor is the resistor that obeys Ohm’s law. Resistor colour code Resistor Colour Codes Yellow Violet Red Silver 4700 ±10 % C CAPACITOR UNIT: Farad (F) • Electrical component that consists of two conductors separated by an insulator or dielectric material. • Its behavior based on phenomenon associated with electric fields, which the source is voltage. • A time-varying electric fields produce a current flow in the space occupied by the fields. • Capacitance is the circuit parameter which relates the displacement current to the voltage. A capacitor with an applied voltage Plates – aluminum foil Dielectric – air/ceramic/paper/mica Plates – aluminum foil Dielectric – air/ceramic/paper/mica Circuit symbols for capacitors (a) Fixed capacitor (b) Variable capacitor Circuit parameters • The amount of charge stored, q = CV. • C is capacitance in Farad, ratio of the charge on one plate to the voltage difference between the plates. But it does not depend on q or V but capacitor’s physical dimensions i.e., A C d = permeability of dielectric in Wb/Am A = surface area of plates in m2 d = distance between the plates m INDUCTOR UNIT: Henry (H) L • Electrical component that opposes any change in electrical current. • Composed of a coil or wire wound around a nonmagnetic core/magnetic core. • Its behavior based on phenomenon associated with magnetic fields, which the source is current. • A time-varying magnetic fields induce voltage in any conductor linked by the fields. • Inductance is the circuit parameter which relates the induced voltage to the current. Typical form of an inductor Circuit symbols for inductors Air-core iron-core Variable iron-core - Ohm’s Law - Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) - Series and Parallel circuit - Voltage Divider Rule (VDR) and Current Divider Rule (CDR) OHM’S LAW Georg Simon Ohm (1787-1854) formulated the relationships among voltage, current, and resistance as follows: The current in a circuit is directly proportional to the applied voltage and inversely proportional to the resistance of the circuit. V IR Calculating Current Vs = 24 V R 1.2 kW V 24 V = 0.02 A = 20 mA I= = R 1200 W Calculating Resistance A Vs = 12 V 0.02 A R V 12 V R= I = = 600 W = 0.6 k W 0.02 A Calculating Voltage A Vs = ? 0.025 A R 470 W V = IR = 0.025 A x 470 W = 11.75 V Calculating Power A V 0.25 A 67.5 V 270 W P = IV = 0.25 A x 67.5 V = 16.9 W P = I2R = 0.25 A x 0.25 A x 270 W = 16.9 W P = V2/R = (67.5 V x 67.5 V) / 270 W = 16.9 W • A branch represents a single element such as a voltage source or a resistor. • A node is the point of connection between two or more branches. • A loop is any closed path in a circuit. • A network with b branches, n nodes, and l independent loops will satisfy the fundamental theorem of network topology: b l n 1 Example: Original circuit Equivalent circuit How many branches, nodes and loops are there? - Ohm’s Law - Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) - Series and Parallel circuit - Voltage Divider Rule (VDR) and Current Divider Rule (CDR) KIRCHHOFF’S LAW • Gustav Robert Kirchhoff (1824 – 1887) • Models relationship between: – circuit element currents (KCL) – circuit element voltages (KVL) • He introduces two laws: – Kirchhoff Current Law (KCL) – Kirchhoff Voltage Law (KVL) Kirchhoff ’s Current Law (KCL) • Current entering node = current exiting • Convention: +i is exiting, -i is entering • For any circuit node: i 0 Kirchhoff ’s Current Law (KCL) Kirchhoff ’s Current Law (KCL) states that the algebraic sum of current entering a node must be equal to that of leaving the same node. Example Determine the current I for the circuit shown in the figure below. I + 4-(-3)-2 = 0 I = -5A We can consider the whole enclosed area as one “node”. This indicates that the actual current for I is flowing in the opposite direction. Kirchhoff ’s Voltage Law (KVL) • voltage increases = voltage decreases • Convention: hit minus (-) side first, write negative • For any circuit loop: v 0 Kirchhoff ’s Voltage Law (KVL) Kirchhoff ’s Voltage Law states that the algebraic sum of voltage drop in a loop must be equal to that of voltage rise in the same loop. Stated it in a different way is that the algebraic sum of all voltages around a loop must be zero. Example • Applying the KVL equation for the circuit of the figure below. va-v1-vb-v2-v3 = 0 V1 = IR1 v2 = IR2 v3 = IR3 va-vb = I(R1 + R2 + R3) va vb I R1 R2 R3 - Ohm’s Law - Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) - Series and Parallel circuit - Voltage Divider Rule (VDR) and Current Divider Rule (CDR) SERIES AND PARALLEL CIRCUIT Resistor below is arranged in series connection: R1 I VS R2 V1 RN V2 VN I VS Req The equivalent resistance for any number of resistors in series connection is the sum of each individual resistor. Req = R1 + R2 + ……….+ RN CURRENT IN SERIES CIRCUIT Current in series circuit is the same as in each circuit element. I I1 I 2 I N VOLTAGE IN SERIES CIRCUIT Voltage (VT) in series circuit is the total voltage of each element circuit. VT V1 V2 .. VN Resistor below is arranged in parallel connection: IS V I1 I2 R1 R2 IN RN IS V Req The equivalent resistance for any number of resistors in parallel connection is obtained by taking the reciprocal of the sum of the reciprocal of each single resistor in the circuit. Equivalent resistance: 1 1 1 1 ............ Req R1 R2 RN Req 1 1 R1 1 R2 ........ 1 RN For the circuit which have two resistors in parallel connection: Req R1 R2 Req 1 1 R1 1 R1 R2 R1 R2 R2 CURRENT IN PARALLEL CIRCUIT • Current in series circuit is equal to the total current for each element circuit I I1 I 2 .. I N VOLTAGE IN PARALLEL CIRCUIT • Voltage (VT) in series circuit is the same as for each element circuit VT V1 V2 VN - Ohm’s Law - Kirchhoff Current Law (KCL) and Kirchhoff Voltage Law (KVL) - Series and Parallel circuit - Voltage Divider Rule (VDR) and Current Divider Rule (CDR) VOLTAGE DIVIDER Whenever voltage has to be divided among resistors in series use voltage divider rule principle. By applying Ohm’s Law: V2 R2 I V I R1 R2 Voltage at resistor R2: V R2 V V2 R2 R1 R2 R1 R2 CURRENT DIVIDER I V _ I1 I2 R1 R2 Whenever current has to be divided among resistors in parallel, use current divider rule principle. By applying Ohm’s Law: R1R2 V I1R1 I 2 R2 I R R 1 2 So, to find current, I1 and I2 : R2 I I1 R R 2 1 R1 I I 2 R R 2 1