Download Chapter 9

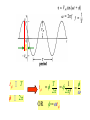
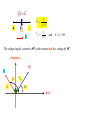
A sinusoidal current source (independent or dependent) produces a current
That varies sinusoidally with time
t
t
T

2
t
OR
T
1




2
2 f

  t 
We define the Root Mean Square value of v(t) or rms as
Square v (t)
calculte the Mean
Take the square Root
The Root Mean Square value of
Expand using trigonometric identity
T  1ms
1
 f   1000 HZ
T
  2 f  2000 rad / s
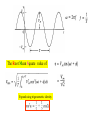
 i (0)  20 cos( )  10  20 cos( )
10 
o

   cos    60
 20 
1
I rms
 i (t )  20 cos(2000 t  60 ) A
20

2
o
 14.44 A
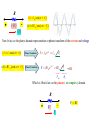
9.2 The Sinusoidal Response
i (t )
3
 v R (t ) 
V S (t )  10 cos(3t  40 )
o

v L (t )


2H

L di  Ri 10 cos(3t  40o )
dt
Solution for i(t) should be a sinusoidal of frequency 3
KVL
i (t )  1.58 cos(3t  31.56 )
o
v R (t )  3.1cos(3t  31.56 )
o
We notice that only the amplitude
and phase change
v L (t )  9.5 cos(3t  58.43o )
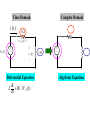
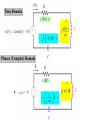
In this chapter, we develop a technique for calculating the response directly without
solving the differential equation
V S (t )
Time Domain
i (t )
Complex Domain
3
 v R (t ) 



v L (t )
2H



Deferential Equation
L di  Ri V S (t )
dt
Algebraic Equation
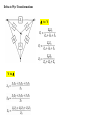
9.3 The phasor
The phasor is a complex number that carries the amplitude and phase angle information
of a sinusoidal function
The phasor concept is rooted in Euler’s identity
e  j   cos( )  j sin( )
Euler’s identity relates the complex exponential function to the trigonometric function
We can think of the cosine function as the real part of the complex exponential and the
sine function as the imaginary part
cos( ) {e j  }
sin( )  {e j  }
Because we are going to use the cosine function on analyzing the sinusoidal steady-state
we can apply
j
cos( ) {e }
e  j   cos( )  j sin( )
cos( ) {e j  }
sin( )  {e j  }
v V m cos(t  ) V m {e j (t  )} V m {e j t e j  }
v {V me j e j t }
We can move the coefficient Vm inside
The quantity
V me j 
is a complex number define to be the phasor
that carries the amplitude and phase angle
of a given sinusoidal function
Phasor Transform
P{V m cos(t  )}  V me j  =V
Were the notation
P{V m cos(t  )}
Is read “ the phasor transform of
V m cos(t  )
Summation Property of Phasor
where v 1, v 2,
(can be shown)
v n are sinusoidal
Since
Next we derive y using phsor method
The VI Relationship for a Resistor
R

v (t )
v (t )  R i (t )

i (t)
Let the current through the resistor be a sinusoidal given as
i (t )  I m cos(t  i )
v (t )  R i (t )  R I m cos(t  i )  R I m cos(t  i )

v (t )  R I m cos(t



i )
voltage phase 
Is also sinusoidal with
amplitude V m  RI m
And phase v  i
The sinusoidal voltage and current in a resistor are in phase
R

v (t )
i (t )  I m cos(t  i )

i (t)
v (t )  R I m cos(t  i )
Now let us see the pharos domain representation or pharos transform of the current and voltage
i (t )  I m cos(t  i )
v (t )  R I m cos(t  i )
Phasor Transform
Phasor Transform
I  I me j   I m
i
V  RI me j 
i
i
 RI m
Vm
i
= RI
v
Which is Ohm’s law on the phasor ( or complex ) domain
R


V
I
V  RI
R
V  RI


V
I
The voltage and the current are in phase
Imaginary
V
Vm
Im
I
 i v   i
Real
The VI Relationship for an Inductor
L

v (t )

v (t )  L di (t )
dt
i (t)
Let the current through the resistor be a sinusoidal given as
i (t )  I m cos(t  i )
v (t )  L di (t )  LI m sin(t  i )
dt
The sinusoidal voltage and current in an inductor are out of phase by 90o
The voltage lead the current by 90o or the current lagging the voltage by 90o
You can express the voltage leading the current by T/4 or 1/4f seconds were T is the period
and f is the frequency
L

v (t )
i (t )  I m cos(t  i )

v (t )  LI m sin(t  i )
i (t)
Now we rewrite the sin function as a cosine function
( remember the phasor is defined in terms of a cosine function)
v (t )  LI m cos(t  i  90o )
The pharos representation or transform of the current and voltage
I  I me j   I m
i (t )  I m cos(t  i )
i
v (t )  LI m cos(t  i
But since
Therefore
 90o )
j 1e j 90  1
o
i
V   L I me
o
i
 j
90o
V  j LI me j   LI me j 90 e j   LI me j (
V m   LI m and
 LI me j  e  j 90  j LI me j 
j ( i 90o )
i
v   i  90o
o
i
i
 90o )
 LI m
Vm
(i  90o )
v
i
j L


V
I
V  j L I
V m   LI m
and
v   i  90o
The voltage lead the current by 90o or the current lagging the voltage by 90o
Imaginary
V
Vm
v
Im
I
i
Real
The VI Relationship for a Capacitor
C

v (t )

i (t ) C dv (t )
dt
i (t)
Let the voltage across the capacitor be a sinusoidal given as
v (t ) V m cos(t  v )
i (t ) C dv (t )   CV m sin(t  v )
dt
The sinusoidal voltage and current in an inductor are out of phase by 90o
The voltage lag the current by 90o or the current leading the voltage by 90o
The VI Relationship for a Capacitor
C

i (t )   CV m sin(t  v )
v (t ) V m cos(t  v )

v (t )
i (t)
The pharos representation or transform of the voltage and current
v
V  V me j   V m
v (t ) V m cos(t  v )
v
i (t )   CV m sin(t  v )   CV m cos(t  v  90o )
I   CV me j  e j 90
 j  CV me j 
o
v
j
V 
I
j C
V m  Im
C

I me j 
i
1e j 90  C
j
and
o
v
j ( 90 )
 I me
C
v   i  90o
i
o
I  LV me j (
 j  CV
 Im
C
Vm
(i 90o )
v
v
90o )
1 j C
V 


V
I
j C
V m  Im
C
I
and
v   i  90o
The voltage lag the current by 90o or the current lead the voltage by 90o
Imaginary
V
I
i
Im
Vm
v
Real
Phasor ( Complex or Frequency) Domain
Time-Domain
Imaginary
R

R
i (t)

v (t )  R i (t )

V
Im
V  RI
I
i (t )  I m cos(t  i )
Real
Imaginary


v
Vm

I
Im
i
Real
I
i (t )  I m cos(t  i )
v (t )  LI m sin(t  i )
V  j L I
v (t )  L di (t )
dt
Imaginary
1 j C
C
v (t )
V
V
i (t)

V  j L I
j L
L
v (t )
I
v   i
v (t )  R I m cos(t  i )

V  RI
Vm

v (t )
V
V
I
i

i (t)

i (t ) C dv (t )
dt
v (t ) V m cos(t  v )
i (t )   CV m sin(t  v )

V
I
V 
Im
V 
Vm
I
j C
v
Real
I
j C
Impedance and Reactance
The relation between the voltage and current on the phasor domain (complex or frequency)
for the three elements R, L, and C we have
V  RI
V  j L I
V 
I
j C

1
j C
I
When we compare the relation between the voltage and current , we note that they are all of
form:
V  ZI
Which the state that the phasor voltage is some complex constant ( Z )
times the phasor current
This resemble ) ‫ ( شبه‬Ohm’s law were the complex constant ( Z ) is called “Impedance” ) ‫(أعاقه‬
Recall on Ohm’s law previously defined , the proportionality content R was real and
called “Resistant” ) ‫(مقاومه‬
V
Z

Solving for ( Z ) we have
I
The Impedance of a resistor is
ZR  R
The Impedance of an indictor is
ZL  j  L
1
ZC 
j C
The Impedance of a capacitor is
In all cases the impedance is measured
in Ohm’s 
V  j L I
V  RI
Z
Impedance
V 
1
j C
I
V
I
The Impedance of a resistor is
ZR  R
The Impedance of an indictor is
ZL  j  L
1
ZC 
j C
The Impedance of a capacitor is
In all cases the impedance is measured
in Ohm’s 
The imaginary part of the impedance is called “reactance”
The reactance of a resistor is
XR  0
We note the “reactance” is associated
with energy storage elements like the
inductor and capacitor
XL   L
The reactance of a capacitor is
XC  1
C
Note that the impedance in general (exception is the resistor) is a function of frequency
The reactance of an inductor is
At  = 0 (DC), we have the following
ZL  j  L  j (0) L  0
ZC 
1
j C

1
 
j (0) C
short
open
Time Domain
Phasor (Complex) Domain
9.5 Kirchhoff’s Laws in the Frequency Domain ( Phasor or Complex Domain)
Consider the following circuit
R2
v 2 (t ) 

R1
Phasor Transformation
+
v 1 (t )
v 3 (t )


L
V 1=V 1e
v 2 (t ) V 2 cos(t  2 )
V 2 =V 2e
v 3(t ) V 3 cos(t  3)
V 3 =V 3e
v 4 (t ) V 4 cos(t  4 )
v 4 (t ) 
j 1
v 1(t ) V 1 cos(t  1)
j 2
j 3
V 4 =V 4e
j 4
v 1(t )  v 2 (t )  v 3(t )  v 4 (t )  0
KVL
C
V 1 cos(t  1)  V 2 cos(t  2 )  V 3 cos(t  3)  V 4 cos(t  4 )  0
j
Using Euler Identity we have {V 1e 1e j t } {V 2e
j
Which can be written as {V 1e 1e j t V 2e
{(V 1e
Factoring e j t
j 1
V 2e
V1
Phasor
So in general
V1 +V 2 + +V n = 0
V2
j 2
j 2 j t
e
V 3e
V3
j 3
j 2 j t
e
j
} {V 3e 3e j t } {V 4e
j
V 3e 3e j t V 4e
V 4e
V4
j 4
j 4 j t
e
)e j t }  0
j 4 j t
e
} 0
} 0
V1 +V 2 +V 3 +V 4 = 0
Can not
be zero
KVL on the phasor
domain
Kirchhoff’s Current Law
A similar derivation applies to a set of sinusoidal current summing at a node
i1(t )  I 1 cos(t  1)
Phasor
Transformation
I 1=I 1e
KCL
j 1
i 2 (t )  I 2 cos(t  2 )
I 2 =I 2e
i n (t )  I n cos(t  n )
j 2
i1(t )  i 2 (t ) 
I 1 +I 2 + +I n = 0
I n =I ne
j n
 i n (t )  0
KCL on the phasor
domain
9.6 Series, Parallel, Simplifications
and Ohm’s law in the phosor domain
Example 9.6 for the circuit shown below the source voltage is sinusoidal
v s (t )  750cos(5000t  30o )
(a) Construct the frequency-domain (phasor, complex) equivalent circuit ?
(b) Calculte the steady state current i(t) ?
The source voltage pahsor transformation or equivalent
o
V s =750 e j 30 =75030
o
The Impedance of the indictor is
Z  j L  j (5000)(32 X 10)  j 160 
The Impedance of the capacitor is
ZC 
L
1
j C

1
  j 40 
j (5000) (5 X 106 )
v s (t )  750cos(5000t  30o )
To Calculate the phasor current I
I  Vs
Z
ab
o
j 30
750
e

90  j 160  j 40
j 30
75030o
750
e


90  j 120
15053.13o
o
i (t )  5cos(5000t  23.13o ) A
 5  23.13o A
and Ohm’s law in the phosor domain
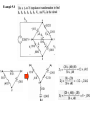
Example 9.7 Combining Impedances in series and in Parallel
i s (t )  8cos(200,000t ) A
(a) Construct the frequency-domain (phasor, complex) equivalent circuit ?
(b) Find the steady state expressions for v,i1, i2, and i3 ? ?
(a)
Delta-to Wye Transformations
D to Y
Y to D
Example 9.8
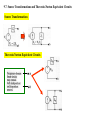
9.7 Source Transformations and Thevenin-Norton Equivalent Circuits
Source Transformations
Thevenin-Norton Equivalent Circuits
Example 9.9
Example 9.10
Source Transformation
KVL
Since
then
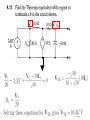
Next we find the Thevenin Impedance
Thevenin Impedance
Find I T interms of VT then form the ratio
Find Ia and Ib interms of VT
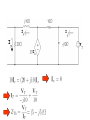
12 60
VT
IT
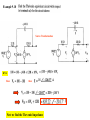
9.8 The Node-Voltage Method
Example 9.11
KCL at node 1
KCL at node 2
(1)
Since
(2)
Two Equations and Two Unknown , solving
To Check the work
9.9 The Mesh-Current Method
Example 9.12
KVL at mesh 1
KVL at mesh 2
Since
(2)
Two Equations and Two Unknown , solving
(1)
9.12 The Phasor Diagram