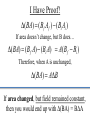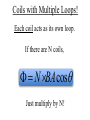Download v - Madison Public Schools

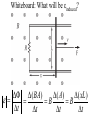
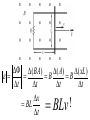
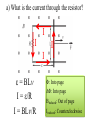
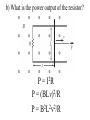
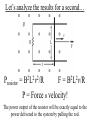
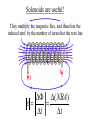
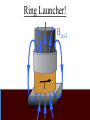
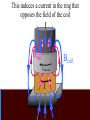
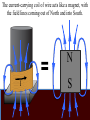
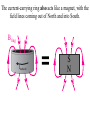
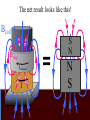
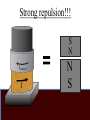
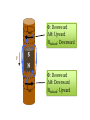
Faraday’s Law
The loop of wire shown below has a radius of 0.2 m, and is in a
magnetic field that is increasing at a rate of 0.5 T/s.
r
Since the area of the
loop is constant,
Δ(BA) = AΔB
DB
DF D(BA)
=A
=
e=
Dt
Dt
Dt
I Have Proof!
D(BA) = (B f A f ) - (Bi Ai )
If area doesn’t change, but B does…
D(BA) = (B f A) - (Bi A) = A(B f - Bi )
Therefore, when A is unchanged,
D(BA) = ADB
If area changed, but field remained constant,
then you would end up with Δ(BA) = BΔA
Whiteboard Warmup!
The loop of wire shown below has a radius of 0.2 m, and is in
a 0.8 T magnetic field. The loop is rotated by 90° in 2
seconds along the dotted line shown. The loop contains a 3 Ω
resistor.
r
a) What is the average induced emf?
b) What is the induced current, and which way does it flow?
Since B and A are constant
DF D(BAcosq )
D(cosq )
e=
=
= BA
Dt
Dt
Dt
cosq f - cosqi = cos(90) - cos(0) = -1
a) ε = 0.05 Volts
b) I = ε/R = 0.016 A counterclockwise
Reverse Rail Gun!
A metal rod is pulled to the right at constant velocity, along
two conducting rails shown below. What is the direction of the
induced current through the circuit as a result?
Φ: Into page
ΔΦ: Into page
Binduced: Out of page
Iinduced: Counterclockwise
Whiteboard: What will be εinduced?
DF D(BA)
D(A)
D(xL)
e=
=
=B
=B
Dt
Dt
Dt
Dt
DF D(BA)
D(A)
D(xL)
e=
=
=B
=B
Dt
Dt
Dt
Dt
Dx
= BL
!
Dt
= BLv
Motional EMF
When the amount of a loop’s area that in a magnetic field is
changing at a constant rate, Faraday’s Law gives the result
e = BLv
• L is the side that is not changing.
• v is the rate of change of the side
that is entering or leaving the field.
Using Motional EMF
In terms of the quantities shown above, write an expression for
a) The current through the resistor, and direction of current.
b) The power output of the resistor in the circuit.
c) The force required to pull the metal bar at constant velocity.
a) What is the current through the resistor?
I
I
I
I
ε = BLv
I = ε/R
I = BLv/R
Φ: Into page
ΔΦ: Into page
Binduced: Out of page
Iinduced: Counterclockwise
b) What is the power output of the resistor?
2
IR
P=
P = (BLv)2/R
P = B2L2v2/R
c) What is the force required to pull the bar at constant speed?
FB
I
Using RHR #2, you can determine that when there
is a current flowing through the circuit, the moving
metal bar will feel a magnetic force to the left.
Therefore, to pull the bar at constant velocity, you must
exactly balance out the magnetic force BIL.
c) What is the force required to pull the bar at constant speed?
FB
I
FB = BIL
FB = B(BLv/R)L
FB = B2L2v/R
In order to pull the
bar at constant
velocity, you must
exactly match this
force by pulling to
the right
Let’s analyze the results for a second…
Presistor = B2L2v2/R
F = B2L2v/R
P = Force x velocity!
The power output of the resistor will be exactly equal to the
power delivered to the system by pulling the rod.
Coils with Multiple Loops!
Each coil acts as its own loop.
If there are N coils,
F = N × BAcosq
Just multiply by N!
Solenoid
Φ = N BA
*
Solenoids are useful!
They multiply the magnetic flux, and therefore the
induced emf, by the number of turns that the wire has
DF D(NBA)
e=
=
Dt
Dt
Ring Launcher!
I
Ring Launcher!
Bcoil
I
This induces a current in the ring that
opposes the field of the coil
Bring
Bcoil
Iinduced
I
The current-carrying coil of wire acts like a magnet, with
the field lines coming out of North and into South.
N
I
S
The current-carrying ring also acts like a magnet, with the
field lines coming out of North and into South.
Bring
Iinduced
S
N
The net result looks like this!
Bcoil
S
N
Bring
Iinduced
I
N
S
Strong repulsion!!!
S
N
Iinduced
I
N
S
Whiteboard: Copper Tube Drop!
S
N
v
a) What will be the direction of
the induced current in each of
these sections of copper tube?
b) Draw the “magnet” that each
of these sections acts like.
c) What will be the result when
the magnet is dropped down the
tube?
Iind
Φ: Downward
ΔΦ: Upward
Binduced: Downward
v
Iind
Φ: Downward
ΔΦ: Downward
Binduced: Upward
v
v
Attracted by the induced
magnet above
v
Repelled from the
induced magnet below
The magnet will fall slowly!!!