Download Operational Amplifiers (Op Amps)

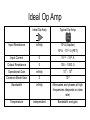
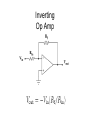
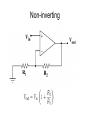
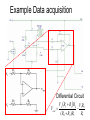
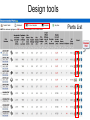
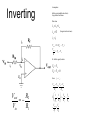
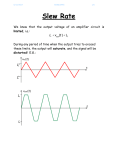
Operational Amplifiers
(Op Amps)
Adnan Pandjou
Hunter Moore
Tyler Randolph
Agenda
•
•
•
•
•
•
•
•
•
Background
Ideal Op Amp
Inverting
Non-inverting
Integrating
Differential
Summing
Applications
Conclusion
Background
•
•
•
Originally designed to perform mathematical
operations in 1940 using vacuum technology
The first integrated op-amp to become widely
available was produced in the late 1960’s by
Fairchild
Wide variety of applications, low cost, and
easily manufactured
Ideal Op Amp
Ideal Op-Amp
Typical Op-Amp
Input Resistance
infinity
106  (bipolar)
109  - 1012  (FET)
Input Current
0
10-12 – 10-8 A
Output Resistance
0
100 – 1000 
Operational Gain
infinity
105 - 109
Common Mode Gain
0
10-5
Bandwidth
infinity
Attenuates and phases at high
frequencies (depends on slew
rate)
Temperature
independent
Bandwidth and gain
Inverting
Op Amp
Non-inverting
Integrating
Inverting op-amp feed back resistor replaced with a capacitor
Input voltage is integrated by using a capacitor
Smoothes out signals and helps to remove offset
Used for PID controllers
Differential
If all of the resistors are equal, the differential op-amp becomes a difference amplifier
Vout=V1-V2
If R4=R3 and R2=R1, then it becomes amplified difference op-amp
Vout=(V2-V1)R3/R1
Summing
Summing amplifiers combine signals by adding directly or scaling and then adding
If all resistors are equal
Vo  V1  V2  V3 
Audio mixers sum several signals with equal gains
Digital-to-analog converters use different resistors to give a weighted sum
LED’s use summing amps to apply a DC off set to AC voltage to keep it in
its linear operating range

Applications
•
•
•
•
Low Pass Filters
High Pass Filters
Offset Comparator
Data acquisition
Low Pass Filter
•Used to filter frequencies above fc
•Second order
•Active
1
fc 
2 R1R2C1C2
High Pass Filter
•Used to filter frequencies below fc
•Second order
•Active
•C2 and R2 switched
1
fc 
2 R1R2C1C2
Offset Comparator
If
U2 
R2
R1  R2
.U1
Output = 0V
If
U2 
5.R1  U1.R2
R1  R2
Output = 5V
•Good for setting thresholds
Offset Comparator
Example
• Setting thresholds for IR
detector
IR detector
Op-amp
R1
R2
Data acquisition
• Signal amplification
• Example (Lab 2)
Amplification of strain gage signal
Example Data acquisition
Differential Circuit
Vout
V 2 R3  R1 R4 V1R3


( R4  R2 ) R1
R1
Where to get Op-amps
for Free
• Companies give free samples
www.national.com
Where to get Op-amps
for Free
•5 (max 5 of each kind) samples per week
Design tools
Design tools
Design tools
Design tools
Parts List
Design tools
Design simulation
Conclusion
• Wide range of application
• Lots of recourses
• Look at other previous student
presentations
Questions?
Appendix
Inverting
Assumptions
Infinite gain (amplification factor)
Large internal resistance
Derivation
i1  i2  ia
ia  0
i2
(Large internal resistance)
i1  i2
V out  K (V B  V A )
V out
 VB  VA
K
ia
i1
VA
K = Infinite gain, therefore
VB  V A
VB  V A  0
VB
From
i1  i 2
,
Vout VA VA  Vin

Rf
Rin
Vout
R2

Vin
R1
 1 1  V
Vin
out
VA 





R R  R R
 in
f 
f
in
V
V
 out  in
R f Rin
Non-Inverting
Assumptions
Infinite gain (amplification factor)
Derivation
Vout  K(Vin  VA )
Vout
 Vin  VA
K
K = Infinite gain, therefore

Vin  V A
Vout  0 VA  0

R2  R1
R1
VA
Vout
V
 in
R2  R1 R1
 R2 
Vout  Vin 1 
 R1 
