* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download An Application of the Inverting Integrator
Quantization (signal processing) wikipedia , lookup
Spectral density wikipedia , lookup
Mains electricity wikipedia , lookup
Voltage optimisation wikipedia , lookup
Dynamic range compression wikipedia , lookup
Control system wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Voltage regulator wikipedia , lookup
Power electronics wikipedia , lookup
Oscilloscope history wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Buck converter wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
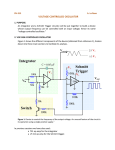
Schmitt trigger wikipedia , lookup
5/15/2017 841021612 1/3 An Application of the Inverting Integrator Note the time average of a signal v (t) over some arbitrary time T is mathematically stated as: 1 average of v (t ) v (t ) T T v (t ) dt 0 Note that this is exactly the form of the output of an op-amp integrator! We can use the inverting integrator to determine the timeaveraged value of some input signal v (t) over some arbitrary time T. For example, say we wish to determine the time-averaged value of the input signal: vin(t) 5 0 -5 1 2 3 4 t 5/15/2017 841021612 2/3 I.E., 5 vin (t ) 5 0 0 t 2 2 t 3 t 3 The time average of this function over a period from 0 < t < T=3 is therefore: 3 1 5 vi (t ) vi (t ) dt 30 3 We could likewise determine this average using an inverting integrator. We select a resistor R and a capacitor C such that the product RC = 3 seconds. The output of this integrator would be: 5t 3 t 1 5t 20 vout (t ) v ( t ) dt in 3 0 3 5 3 0 t 2 2 t 3 t 3 5/15/2017 841021612 v o (t ) 0 1 3 2 3/3 4 t 5 3 10 3 Note that the value of the output voltage at t =3 is: 3 1 5 vout (t 3) v ( t ) dt in 3 0 3 The time-averaged value (times –1)! Thus, we can use the inverting integrator, along with a voltage sampler (e.g., A to D converter) to determine the time-averaged value of a function over some time period T. vin (t) vo (t) t =T=RC vout (t T ) vout (t )