Download Engineering Systems - University of Detroit Mercy

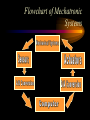
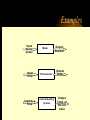
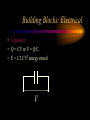
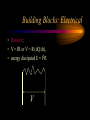
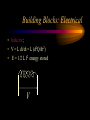
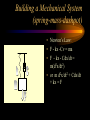
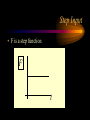
Engineering Systems
Shuvra Das
University of Detroit Mercy
Summary
•
•
•
•
•
•
Engineering systems
Approach to analyze systems
System components
Types of systems
System equations
System responses
Flowchart of Mechatronic
Systems
Relevant questions: Systems!
• A motor is switched on: “How will the rotation of
the shaft vary with time?”
• A hydraulic system opens a valve to allow a liquid
to flow into a tank: “How will the water level vary
with time?”
• A crash has occurred: “How fast will the airbag
system deploy?”
• To answer these questions an understanding of the
system behavior is necessary.
Engineering System
• A system consists of multiple components that
work together to perform a task. Although a
system may be made of many components it can
be represented as a “black-box” with an input and
an output.
– temperature measuring system,
– transmission system
– hydraulic system,
– lighting system,heating system
– suspension system, etc.
Examples
Input
Electric
Motor
power
Input
Temp.
Input Req.
Temp.
Thermometer
Central Heating
System
Output
Rotation
Output
Temp.
Output
Temp. at
the set
value
Stages of Dynamic System
Investigation
• Physical Modeling
– Imagine a simple physical model that will match
closely the behavior of the system
• Equations of Motion
– Develop Mathematical Model to describe the physical
model
• Dynamic Behavior
– Study the dynamic behavior of the physical model
• Design Decisions
– choose physical parameters of the system such
that it will behave as desired
Example
SCHEMATIC DIAGRAM OF HYDRO-POWER
STEERING SYSTEM
Block-diagram of subsystems
ALI KEYHANI MODEL :
Mechanical subsystem
• The equations for the steering column, pinion and
rack can be written :
Equation 1 :
Equation 2 :
ALI KEYHANI MODEL :
Mechanical subsystem
Where Td=Torque generated by the driver,
Theta1=rotational displacement for the steering column,
K2=tire stiffness
B2=Viscous damping coefficient
B1=friction constant of the upper-steering column
X=displacement of the rack
m= mass of pinion
Ap= Piston area
K1=torsion bar stiffness
J1=Inertia constant of the upper steering column
ALI KEYHANI MODEL :
Mechanical subsystem
The following assumptions were made :
-the
pressure forces on the spool are neglected.
-the stiffness of the steering column is infinite.
-the inertia of the lower steering column (valve spool and
pinion) is lumped into the rack mass.
ALI KEYHANI MODEL
hydraulic subsystem
ALI KEYHANI MODEL
hydraulic subsystem
By applying the orifice equations to the rotary valve metering orifices and mass conservation
equations to the entire hydraulic subsystem the following equation are obtained :
Equation 1 :
Equation 2 :
Equation 3 :
ALI KEYHANI MODEL
hydraulic subsystem
Where Ps and Po =supply and return pressure of the
pump.
Pl and Pr = cylinder pressure on the left and right side.
Q = supply flow rate of the pump
A1 and A2 are the metering orifice area
Rho = density of the fluid
Beta=bulk modulus of fluid
L=length of the cylinder
Cd= discharge co-efficient
Approximations in Physical
Modeling
Approximation
Neglect small Effects
Mathematical Simplification
Reduces number and complexity of
differential equations
Reduces number and complexity of
differential equations
Assume environment
independent of system
motions
Replace distributed
Leads to ordinary rather than partial differential
characteristics by lumped
equations
elements
Assume linear relationships Makes equations linear (allows superposition of
Solutions)
Assume constant
Leads to constant coefficients of diff. Eqns.
parameters
Neglect uncertainty and
Avoids statistical treatment
noise
Examples of approximations
•
•
•
•
•
•
Neglect small effects
Independent environment
Lumped characteristics
linear relationships
constant parameters
Neglect uncertainty and
noise
• Realistic physical model
leads to non-linear PDEs
with time and space
varying parameters
• Simplifying assumptions
led to ODEs with constant
coefficients
• Engineering
Judgement is key!
From Physical Model to
Mathematical Model
• Dynamic Equilibrium Relations: balance of forces, flow
rates, energy, etc. which must exist for the system and subsystems.
• Compatibility Relations: how motions of the system
elements are interrelated because of the way they are
interconnected.
• Physical Variables:Selection of precise physical variables
(velocity, force, voltage, pressure, flow rate, etc.) with
which to describe the instantaneous state of the system.
From Physical Model to
Mathematical Model
• Physical Laws: Natural Physical laws which
individual elements of the system obey, e.g.
– Mechanical relations between force and motion
– electrical relations between current and voltage
– electromechanical relations between force and magnetic
field
– thermodynamic relations between temperature,
pressure, internal energy, etc.
– These are also called constitutive physical
relationships!
Classification of Physical
Variables
• Through Variables (one-point variables) measure
the transmission of something through an element,
e.g.
– electric current through a resistor
– fluid flow through a duct
– force through a spring
– heat flux flowing through
Classification of Physical
Variables
• Across Variables (two-point variables) measures
the difference in state between the ends of an
element, e.g.
– voltage drop across a resistor
– pressure drop between the ends of a duct
– difference in velocity between the ends of a
damper
– temperature difference
Equilibrium Relations
• Are always relations among through
variables
–
–
–
–
Kirchoff’s current law (at an electrical node)
continuity of fluid flow
equilibrium of forces meeting at a point
heat flux balance
Compatibility Relations
• Are always relations among “across
variables”
– Kirchoff’s voltage law around a circuit
– pressure drop across all the connected stages of
a fluid system
– geometric compatibility in a mechanical system
Physical Relations
• Are relations between through and across
variables of each individual element, e.g.
• f = k.x for a spring
• I=V/R for a resistor
System Components
•
•
•
•
•
•
•
spring
mass
damper
capacitor
Voltage generator
resistor
inductor
• Hydraulic valves
• …..
• A real system, may be
broken down into
components that
behave like one of the
basic components
Mechanical Quantities
•
•
•

F=force
T=torque
x=displacement
q = angular
displacement
 dx/dt=v=velocity
 dq/dt=w=angular
velocity
• dv/dt=a=acceleration
• dw/dt=a=angular
acceleration
• I=inertia
• m=mass
• k=spring constant
• C=damping coefficient
Electrical Quantities
•
•
•
•
•
•
V=voltage
Q=charge
I=current
L=inductance
C=capacitance
R=resistance
Building Blocks: Mechanical
• Translational:
– spring;
– F = kx (force displacement relationship),
– E= 1/2(F2/k), energy stored
F
Building Blocks: Mechanical
• Translational:
– dashpot (damper);
– F = C v (C(dx/dt)) (Force-velocity relationship)
– E = Cv 2 energy dissipated
F
Building Blocks: Mechanical
• Translational:
– mass;
– F = ma = m(d2x/dt2)
– E = 1/2 mv2 , Kinetic Energy
F
Building Blocks: Mechanical
• Rotational:
– Spring;
– T = k q,
– E = 1/2 (T2/k), energy stored
T
Building Blocks: Mechanical
• Rotational:
– dashpot;
– T = C w = C dq/dt
– P = Cw2 energy dissipated
T
Building Blocks: Mechanical
• Rotational:
– Moment of Intertia;
– T = I d2 q/dt2
– E =1/2 I w2 , Kinetic energy
T
Building Blocks: Electrical
• Capacitor;
• Q = CV or V = Q/C,
• E = 1/2 CV2 energy stored
V
Building Blocks: Electrical
• Resistor;
• V = IR or V = R (dQ/dt),
• energy dissipated E = I2R
V
Building Blocks: Electrical
• Inductor;
• V = L di/dt = L (d2Q/dt2)
• E = 1/2 L I2 energy stored
V
Mechanical and Electrical
Quantities
Symbol
Mechanical Quantity
Symbol
Electrical Quantity
m
I
mass
Moment of Inertia
L
Inductance
k
Spring Constant
(linear and rotational)
1/C
Reciprocal of Capacitance
C
Damping Coeff.
R
Resistance
F
T
Force
Torque
V
Voltage
x
q
Translational motion
Rotational motion
Q
Charge
dx/dt
dq/dt
Linear velocity
Angular velocity
dQ/dt = i
Current
d2x/dt2
d2q /dt2
Acceleration (linear)
Acceleration (angular)
d2Q/dt2
Rate of change of current
Thermal System
•
•
•
•
T = Temperature
q = heat flux
R=thermal resistance
Conduction, R=L/Ak, A = cross-sectional area, L=length
conducted over, k = thermal conductivity
• Convection, R=1/Ah, A = convective surface, h =
convective heat transfer coefficient
• C=thermal capacitance, mCp (mass X specific heat
capacity)
Thermal System
•
•
•
•
q = (T2-T1)/R
q=Ak(T2-T1)/L; conduction
q=Ah(T2-T1); convection
q1-q2=mCp(dT/dt), q1-q2= rate of change
of internal energy
Hydraulic Systems
• We will not deal with Hydraulic systems
here…...
Types of Systems
• Zeroth order systems
• First order systems
• Second order systems
Zeroth order systems
First -order systems:
examples
First -order systems:
examples
Example of a First order system
• Temperature measuring devices (e.g.
thermocouple or a thermometer) are first-order
systems.
• If a thermometer is dipped in a liquid:
# mCp dT/dt = (Ak/L) (TL -T)
• where m = mass of bulb, Cp is the specific heat
capacity, T is the current temperature of the
mercury, A is the surface area of the bulb, k is its
thermal conductivity, L is the wall thickness, and
TL is the temperature of the liquid.
First order system
• Rewritten:
# mCp dT/dt + (Ak/L) T = (Ak/L) (TL)
• This is a first order system that has been subjected
to a step input (which is the right hand side of the
above equation)
• When this is integrated and initial conditions applied the
solution of this system is an exponential function:
# T = TL + [T0-TL] e-t/t
First order system
• T = TL + [T0-TL] e-t/t
• T0 is the temperature of the bulb at intial time; and
t, the time constant, is written as (mCpL/Ak).
• Response of a First order system to a step
input(decaying and progressing)
5
5
4
4.9
4.8
3
Series1
2
4.7
Series1
4.6
1
4.5
0
4.4
0
0.5
1
0
0.5
1
First order system
• Steady state value is TL (target).
• How soon is this value reached ? (imp. Question)
• The answer lies in the magnitude of the time
constant (=mCpL/Ak, in this case).
• Time constant is defined as the time required to
complete 63.2% of the process, i.e. if the
temperature has to rise from 10 degrees to 70
degrees, time constant is the time required to reach
(10 +63.2%of the interval) 47.92 degrees.
Time Constant
• The smaller the time constant, the faster will the
system respond and the larger the time constant
the slower will the system respond.
Amount of time spent
1 time constant
2 time constant
3 time constant
4 time constant
% of the process completed
63.2%
86.5%
95%
98.2 %
Second-order Systems: examples
Building a Mechanical System
(spring-mass-dashpot)
• Newton’s Law:
• F - kx -Cv = ma
• F - kx - Cdx/dt =
m(d2x/dt2)
• or m d2x/dt2 + Cdx/dt
+ kx = F
Building an Electrical System
(LRC Circuit)
• Kirchoff’s law
• total current flowing
towards a junction =total
current flowing out of a
junction
• In a closed system sum of
potential drops across
each component =applied
emf.
• L d2Q/dt2 + RdQ/dt
+ Q/C = Emf = V
Second order systems
• These are all second order systems since they are
described by a second order differential equation.
• If the mass or the inductance is removed from the
second order systems shown above they become
first order systems.
• While such an electrical system makes sense the
mechanical system without mass is unrealistic.
Second Order Systems
• m d2x/dt2 + Cdx/dt + kx = F
• The solution has two components a CF and PI
• CF: Complementary function; solution with no F
m d2x/dt2 + Cdx/dt + kx = 0
• PI: Particular Integral; solution with F;
– m d2x/dt2 + Cdx/dt + kx = F
• PI is dictated by the nature of F
Finding CF
• Assuming the solution form to be x(t) =
Aelt
• (ml2 + Cl+ k) Aelt = 0 >> ml2 + Cl+ k= 0
• Roots of the quadratic equation are:
• l =  C   C   k
2
1
2m
 2m 
m
2
C
k
 C 
l2 = 
 
 
2m
 2m  m
Finding CF
2
k C
k C
k
l1 = 

(
)
m 2 mk
m 4mk
m
2
k C
k C
k
l2 = 

(
)
m 2 mk
m 4mk
m
l1 = (  
l2 = (  

2
 1)w n
 2  1)w n
l1 = w n  w 2 n  2   w n2
l2 = w n  w 2 n  2   w n2
 z=damping ratio
 wn=natural frequency
Finding CF….
• The solution takes a distinct form depending upon
the values under the square-root sign
• When there is no damping in the system, C=0
(z=0)and both the roots are imaginary
• solution:
k
k
xCF = ACos(
t )  BSin (
t)
m
m
• where A and B are constants determined from
Finding CF...
• This motion represents pure undamped
oscillatory motion with natural frequency of
wn =
k
m
Undamped System
10
5
0
Series1
0
-5
-10
2
4
6
Finding CF
• When C is non-zero:
• 0<z<1,underdamped, the roots l1 and l2 are imaginary
and
– xCF = exp(zwnt)(Pcoswt + Qsinwt), w=damped
frequency
w = w n (1  z 2 )
• A&B or P&Q are determined from initial
conditions
Underdamped System
8
6
4
2
Series1
0
-2 0
-4
2
4
6
Finding CF
 z =1, critically damped, the roots l1 and l2 are equal
xCF=(At+B)exp(l1)= (At+B)exp(-wnt)=
A&B or P&Q are determined from initial
conditions
Critically Damped System
4
3.5
3
2.5
2
1.5
1
0.5
0
Series1
0
2
4
6
Finding CF
 z >1, overdamped, roots the roots l1 and l2 are real and
unequal
xCF=Aexp(l1)+Bexp(l2)
A&B or P&Q are determined from initial
conditions
Finding PI: Interesting
Questions!
• How do systems behave with time when
subject to some disturbance ?
• How do systems behave when a certain
input is provided ?
• What are some expected inputs?
• What do the outputs look like?
Response of Systems
• Natural response and Forced Response
• Natural: No input to the system (system acts on its own),
e.g. water flowing out of a tank when a valve is kept open.
• Forced: water flowing out of a tank while there is input
flow from another source.
• Transient and Steady State Response
• Transient: Response that dies after a short interval of time
• Steady State: Response that remains after all transient
response died.
Second Order Systems
• m d2x/dt2 + Cdx/dt + kx = F
• The solution has two components a CF and PI
• CF: Complementary function; solution with no F
m d2x/dt2 + Cdx/dt + kx = 0
• PI: Particular Integral; solution with F;
– m d2x/dt2 + Cdx/dt + kx = F
• PI is dictated by the nature of F
Step Input
• F is a step function
F
t
Response
• The solution mirrors the nature of the
forcing function
• Therefore the particular integral is F/k
• So the total solution is the XCF +XPI
• XCF has different forms based on the nature of the system,
underdamped, critically damped, overdamped, etc.
• XPI is dependent on the forcing function
Step Response
• Rise time (tr): time taken
to go from zero to steady
state value
• Peak time (tp): time taken
to hit first peak
• Overshoot: maximum
amount by which system
overshoots steady state
value.
• Settling time (ts): time
taken for oscillations to
reach 2% of steady state.