* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Engineering Systems - University of Detroit Mercy
Dynamical system wikipedia , lookup
Renormalization group wikipedia , lookup
Fluid dynamics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Routhian mechanics wikipedia , lookup
Classical central-force problem wikipedia , lookup
Heat transfer physics wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Seismometer wikipedia , lookup
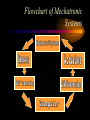
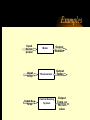
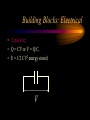
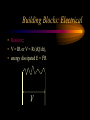
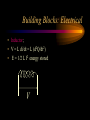
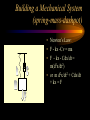
Engineering Systems Shuvra Das University of Detroit Mercy Summary • • • • • • Engineering systems Approach to analyze systems System components Types of systems System equations System responses Flowchart of Mechatronic Systems Relevant questions: Systems! • A motor is switched on: “How will the rotation of the shaft vary with time?” • A hydraulic system opens a valve to allow a liquid to flow into a tank: “How will the water level vary with time?” • A crash has occurred: “How fast will the airbag system deploy?” • To answer these questions an understanding of the system behavior is necessary. Engineering System • A system consists of multiple components that work together to perform a task. Although a system may be made of many components it can be represented as a “black-box” with an input and an output. – temperature measuring system, – transmission system – hydraulic system, – lighting system,heating system – suspension system, etc. Examples Input Electric Motor power Input Temp. Input Req. Temp. Thermometer Central Heating System Output Rotation Output Temp. Output Temp. at the set value Stages of Dynamic System Investigation • Physical Modeling – Imagine a simple physical model that will match closely the behavior of the system • Equations of Motion – Develop Mathematical Model to describe the physical model • Dynamic Behavior – Study the dynamic behavior of the physical model • Design Decisions – choose physical parameters of the system such that it will behave as desired Example SCHEMATIC DIAGRAM OF HYDRO-POWER STEERING SYSTEM Block-diagram of subsystems ALI KEYHANI MODEL : Mechanical subsystem • The equations for the steering column, pinion and rack can be written : Equation 1 : Equation 2 : ALI KEYHANI MODEL : Mechanical subsystem Where Td=Torque generated by the driver, Theta1=rotational displacement for the steering column, K2=tire stiffness B2=Viscous damping coefficient B1=friction constant of the upper-steering column X=displacement of the rack m= mass of pinion Ap= Piston area K1=torsion bar stiffness J1=Inertia constant of the upper steering column ALI KEYHANI MODEL : Mechanical subsystem The following assumptions were made : -the pressure forces on the spool are neglected. -the stiffness of the steering column is infinite. -the inertia of the lower steering column (valve spool and pinion) is lumped into the rack mass. ALI KEYHANI MODEL hydraulic subsystem ALI KEYHANI MODEL hydraulic subsystem By applying the orifice equations to the rotary valve metering orifices and mass conservation equations to the entire hydraulic subsystem the following equation are obtained : Equation 1 : Equation 2 : Equation 3 : ALI KEYHANI MODEL hydraulic subsystem Where Ps and Po =supply and return pressure of the pump. Pl and Pr = cylinder pressure on the left and right side. Q = supply flow rate of the pump A1 and A2 are the metering orifice area Rho = density of the fluid Beta=bulk modulus of fluid L=length of the cylinder Cd= discharge co-efficient Approximations in Physical Modeling Approximation Neglect small Effects Mathematical Simplification Reduces number and complexity of differential equations Reduces number and complexity of differential equations Assume environment independent of system motions Replace distributed Leads to ordinary rather than partial differential characteristics by lumped equations elements Assume linear relationships Makes equations linear (allows superposition of Solutions) Assume constant Leads to constant coefficients of diff. Eqns. parameters Neglect uncertainty and Avoids statistical treatment noise Examples of approximations • • • • • • Neglect small effects Independent environment Lumped characteristics linear relationships constant parameters Neglect uncertainty and noise • Realistic physical model leads to non-linear PDEs with time and space varying parameters • Simplifying assumptions led to ODEs with constant coefficients • Engineering Judgement is key! From Physical Model to Mathematical Model • Dynamic Equilibrium Relations: balance of forces, flow rates, energy, etc. which must exist for the system and subsystems. • Compatibility Relations: how motions of the system elements are interrelated because of the way they are interconnected. • Physical Variables:Selection of precise physical variables (velocity, force, voltage, pressure, flow rate, etc.) with which to describe the instantaneous state of the system. From Physical Model to Mathematical Model • Physical Laws: Natural Physical laws which individual elements of the system obey, e.g. – Mechanical relations between force and motion – electrical relations between current and voltage – electromechanical relations between force and magnetic field – thermodynamic relations between temperature, pressure, internal energy, etc. – These are also called constitutive physical relationships! Classification of Physical Variables • Through Variables (one-point variables) measure the transmission of something through an element, e.g. – electric current through a resistor – fluid flow through a duct – force through a spring – heat flux flowing through Classification of Physical Variables • Across Variables (two-point variables) measures the difference in state between the ends of an element, e.g. – voltage drop across a resistor – pressure drop between the ends of a duct – difference in velocity between the ends of a damper – temperature difference Equilibrium Relations • Are always relations among through variables – – – – Kirchoff’s current law (at an electrical node) continuity of fluid flow equilibrium of forces meeting at a point heat flux balance Compatibility Relations • Are always relations among “across variables” – Kirchoff’s voltage law around a circuit – pressure drop across all the connected stages of a fluid system – geometric compatibility in a mechanical system Physical Relations • Are relations between through and across variables of each individual element, e.g. • f = k.x for a spring • I=V/R for a resistor System Components • • • • • • • spring mass damper capacitor Voltage generator resistor inductor • Hydraulic valves • ….. • A real system, may be broken down into components that behave like one of the basic components Mechanical Quantities • • • F=force T=torque x=displacement q = angular displacement dx/dt=v=velocity dq/dt=w=angular velocity • dv/dt=a=acceleration • dw/dt=a=angular acceleration • I=inertia • m=mass • k=spring constant • C=damping coefficient Electrical Quantities • • • • • • V=voltage Q=charge I=current L=inductance C=capacitance R=resistance Building Blocks: Mechanical • Translational: – spring; – F = kx (force displacement relationship), – E= 1/2(F2/k), energy stored F Building Blocks: Mechanical • Translational: – dashpot (damper); – F = C v (C(dx/dt)) (Force-velocity relationship) – E = Cv 2 energy dissipated F Building Blocks: Mechanical • Translational: – mass; – F = ma = m(d2x/dt2) – E = 1/2 mv2 , Kinetic Energy F Building Blocks: Mechanical • Rotational: – Spring; – T = k q, – E = 1/2 (T2/k), energy stored T Building Blocks: Mechanical • Rotational: – dashpot; – T = C w = C dq/dt – P = Cw2 energy dissipated T Building Blocks: Mechanical • Rotational: – Moment of Intertia; – T = I d2 q/dt2 – E =1/2 I w2 , Kinetic energy T Building Blocks: Electrical • Capacitor; • Q = CV or V = Q/C, • E = 1/2 CV2 energy stored V Building Blocks: Electrical • Resistor; • V = IR or V = R (dQ/dt), • energy dissipated E = I2R V Building Blocks: Electrical • Inductor; • V = L di/dt = L (d2Q/dt2) • E = 1/2 L I2 energy stored V Mechanical and Electrical Quantities Symbol Mechanical Quantity Symbol Electrical Quantity m I mass Moment of Inertia L Inductance k Spring Constant (linear and rotational) 1/C Reciprocal of Capacitance C Damping Coeff. R Resistance F T Force Torque V Voltage x q Translational motion Rotational motion Q Charge dx/dt dq/dt Linear velocity Angular velocity dQ/dt = i Current d2x/dt2 d2q /dt2 Acceleration (linear) Acceleration (angular) d2Q/dt2 Rate of change of current Thermal System • • • • T = Temperature q = heat flux R=thermal resistance Conduction, R=L/Ak, A = cross-sectional area, L=length conducted over, k = thermal conductivity • Convection, R=1/Ah, A = convective surface, h = convective heat transfer coefficient • C=thermal capacitance, mCp (mass X specific heat capacity) Thermal System • • • • q = (T2-T1)/R q=Ak(T2-T1)/L; conduction q=Ah(T2-T1); convection q1-q2=mCp(dT/dt), q1-q2= rate of change of internal energy Hydraulic Systems • We will not deal with Hydraulic systems here…... Types of Systems • Zeroth order systems • First order systems • Second order systems Zeroth order systems First -order systems: examples First -order systems: examples Example of a First order system • Temperature measuring devices (e.g. thermocouple or a thermometer) are first-order systems. • If a thermometer is dipped in a liquid: # mCp dT/dt = (Ak/L) (TL -T) • where m = mass of bulb, Cp is the specific heat capacity, T is the current temperature of the mercury, A is the surface area of the bulb, k is its thermal conductivity, L is the wall thickness, and TL is the temperature of the liquid. First order system • Rewritten: # mCp dT/dt + (Ak/L) T = (Ak/L) (TL) • This is a first order system that has been subjected to a step input (which is the right hand side of the above equation) • When this is integrated and initial conditions applied the solution of this system is an exponential function: # T = TL + [T0-TL] e-t/t First order system • T = TL + [T0-TL] e-t/t • T0 is the temperature of the bulb at intial time; and t, the time constant, is written as (mCpL/Ak). • Response of a First order system to a step input(decaying and progressing) 5 5 4 4.9 4.8 3 Series1 2 4.7 Series1 4.6 1 4.5 0 4.4 0 0.5 1 0 0.5 1 First order system • Steady state value is TL (target). • How soon is this value reached ? (imp. Question) • The answer lies in the magnitude of the time constant (=mCpL/Ak, in this case). • Time constant is defined as the time required to complete 63.2% of the process, i.e. if the temperature has to rise from 10 degrees to 70 degrees, time constant is the time required to reach (10 +63.2%of the interval) 47.92 degrees. Time Constant • The smaller the time constant, the faster will the system respond and the larger the time constant the slower will the system respond. Amount of time spent 1 time constant 2 time constant 3 time constant 4 time constant % of the process completed 63.2% 86.5% 95% 98.2 % Second-order Systems: examples Building a Mechanical System (spring-mass-dashpot) • Newton’s Law: • F - kx -Cv = ma • F - kx - Cdx/dt = m(d2x/dt2) • or m d2x/dt2 + Cdx/dt + kx = F Building an Electrical System (LRC Circuit) • Kirchoff’s law • total current flowing towards a junction =total current flowing out of a junction • In a closed system sum of potential drops across each component =applied emf. • L d2Q/dt2 + RdQ/dt + Q/C = Emf = V Second order systems • These are all second order systems since they are described by a second order differential equation. • If the mass or the inductance is removed from the second order systems shown above they become first order systems. • While such an electrical system makes sense the mechanical system without mass is unrealistic. Second Order Systems • m d2x/dt2 + Cdx/dt + kx = F • The solution has two components a CF and PI • CF: Complementary function; solution with no F m d2x/dt2 + Cdx/dt + kx = 0 • PI: Particular Integral; solution with F; – m d2x/dt2 + Cdx/dt + kx = F • PI is dictated by the nature of F Finding CF • Assuming the solution form to be x(t) = Aelt • (ml2 + Cl+ k) Aelt = 0 >> ml2 + Cl+ k= 0 • Roots of the quadratic equation are: • l = C C k 2 1 2m 2m m 2 C k C l2 = 2m 2m m Finding CF 2 k C k C k l1 = ( ) m 2 mk m 4mk m 2 k C k C k l2 = ( ) m 2 mk m 4mk m l1 = ( l2 = ( 2 1)w n 2 1)w n l1 = w n w 2 n 2 w n2 l2 = w n w 2 n 2 w n2 z=damping ratio wn=natural frequency Finding CF…. • The solution takes a distinct form depending upon the values under the square-root sign • When there is no damping in the system, C=0 (z=0)and both the roots are imaginary • solution: k k xCF = ACos( t ) BSin ( t) m m • where A and B are constants determined from Finding CF... • This motion represents pure undamped oscillatory motion with natural frequency of wn = k m Undamped System 10 5 0 Series1 0 -5 -10 2 4 6 Finding CF • When C is non-zero: • 0<z<1,underdamped, the roots l1 and l2 are imaginary and – xCF = exp(zwnt)(Pcoswt + Qsinwt), w=damped frequency w = w n (1 z 2 ) • A&B or P&Q are determined from initial conditions Underdamped System 8 6 4 2 Series1 0 -2 0 -4 2 4 6 Finding CF z =1, critically damped, the roots l1 and l2 are equal xCF=(At+B)exp(l1)= (At+B)exp(-wnt)= A&B or P&Q are determined from initial conditions Critically Damped System 4 3.5 3 2.5 2 1.5 1 0.5 0 Series1 0 2 4 6 Finding CF z >1, overdamped, roots the roots l1 and l2 are real and unequal xCF=Aexp(l1)+Bexp(l2) A&B or P&Q are determined from initial conditions Finding PI: Interesting Questions! • How do systems behave with time when subject to some disturbance ? • How do systems behave when a certain input is provided ? • What are some expected inputs? • What do the outputs look like? Response of Systems • Natural response and Forced Response • Natural: No input to the system (system acts on its own), e.g. water flowing out of a tank when a valve is kept open. • Forced: water flowing out of a tank while there is input flow from another source. • Transient and Steady State Response • Transient: Response that dies after a short interval of time • Steady State: Response that remains after all transient response died. Second Order Systems • m d2x/dt2 + Cdx/dt + kx = F • The solution has two components a CF and PI • CF: Complementary function; solution with no F m d2x/dt2 + Cdx/dt + kx = 0 • PI: Particular Integral; solution with F; – m d2x/dt2 + Cdx/dt + kx = F • PI is dictated by the nature of F Step Input • F is a step function F t Response • The solution mirrors the nature of the forcing function • Therefore the particular integral is F/k • So the total solution is the XCF +XPI • XCF has different forms based on the nature of the system, underdamped, critically damped, overdamped, etc. • XPI is dependent on the forcing function Step Response • Rise time (tr): time taken to go from zero to steady state value • Peak time (tp): time taken to hit first peak • Overshoot: maximum amount by which system overshoots steady state value. • Settling time (ts): time taken for oscillations to reach 2% of steady state.