* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 20120720-EE235-Lecture18
Survey
Document related concepts
Transcript
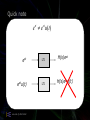
Signals and Systems EE235 Lecture 18 Leo Lam © 2010-2012 Today’s scary menu • Transfer Functions • LCCDE! Leo Lam © 2010-2012 LTI system transfer function est H(s)est LTI H ( s) h( )e s d • s is complex • H(s): two-sided Laplace Transform of h(t) Leo Lam © 2010-2012 3 LTI system transfer function est LTI H(s)est LTI y(t ) AH ( jw)e jwt • Let s=jw x(t ) Ae jwt • LTI systems preserve frequency • Complex exponential output has same frequency as the complex exponential input Leo Lam © 2010-2012 4 LTI system transfer function • Example: x(t ) Ae jwt LTI 1 jwt x(t ) cos(wt ) e e jwt 2 y(t ) AH ( jw)e jwt 1 y (t ) H ( jw )e jwt H ( jw )e jwt 2 • For real systems (h(t) is real): H ( jw ) H ( jw ) y(t ) Aw cos(wt ) • where Aw H ( jw) and H ( jw ) • LTI systems preserve frequency Leo Lam © 2010-2012 5 Importance of exponentials • Makes life easier • Convolving with est is the same as multiplication • Because est are eigenfunctions of LTI systems • cos(wt) and sin(wt) are real • Linked to est Leo Lam © 2010-2012 6 Quick note e e u(t ) st est estu(t) Leo Lam © 2010-2012 st LTI LTI H(s)est H(s)estu(t) 7 Which systems are not LTI? e e 2 t 2 t T 5e 2 t jt 2 t T 5e e NOT LTI cos(3t ) T cos(3 t ) NOT LTI cos(3t ) T sin(3t ) cos(3t ) T 0 cos(3t ) T e Leo Lam © 2010-2012 2 t cos(3t ) NOT LTI 8 Summary • Eigenfunctions/values of LTI System Leo Lam © 2010-2012 LCCDE, what will we do • Why do we care? • Because it is everything! • Represents LTI systems • Solve it: Homogeneous Solution + Particular Solution • Test for system stability (via characteristic equation) • Relationship between HS (Natural Response) and Impulse response • Using exponentials est Leo Lam © 2010-2012 10 Circuit example • Want to know the current i(t) around the circuit C • Resistor E RI R • Capacitor • Inductor Leo Lam © 2010-2012 Q EC C dQ I dt dI EL L dt R L E(t) = E0 sin wt 11 Circuit example • Kirchhoff’s Voltage Law (KVL) C dI Q L RI E0 sin wt dt C EC d 2I dI 1 dQ L 2 R E0w cos wEt dt C dt dt R R 2 d I dI 1 L 2 R I E0w cos wt dt dt C EL L RI E(t) = E0 sin wt input output Leo Lam © 2010-2012 Q C 12 dI dt L Differential Eq as LTI system x(t) T y(t) • Inputs and outputs to system T have a relationship defined by the LTI system: • Let “D” mean d()/dt (a2D2+a1D+a0)y(t)=(b2D2+b1D+b0)x(t) Defining Q(D) Leo Lam © 2010-2012 Defining P(D) 13 Differential Eq as LTI system (example) x(t) T y(t) • Inputs and outputs to system T have a relationship defined by the LTI system: • Let “D” mean d()/dt Leo Lam © 2010-2012 14 Differential Equation: Linearity • Define: • Can we show that: • What do we need to prove? d ( y1 (t ) y2 (t )) y (t ) ak1 x1 (t ) k 2 x2 (t ) b dt Leo Lam © 2010-2012 15 Differential Equation: Time Invariance • System works the same whenever you use it • Shift input/output – Proof • Example: dx(t ) y (t ) dt • Time shifted system: • Time invariance? • Yes: substitute dx(t t0 ) y (t t0 ) dt for t (time shift the input) dx ( ) y ( ) d Leo Lam © 2010-2012 16 Differential Equation: Time Invariance • Any pure differential equation is a timeinvariant system: • Are these linear/time-invariant? Linear, time-invariant Linear, not TI Non-Linear, TI Linear, time-invariant Linear, time-invariant Linear, not TI Leo Lam © 2010-2012 17 LTI System response • A little conceptual thinking • Time: t=0 Unknown past T Initial condition zero-input response (t) Input x(t) T zero-state output (t) • Linear system: Zero-input response and Zero-state output do not affect each other Total response(t)=Zero-input response (t)+Zero-state output(t) Leo Lam © 2010-2012 18 Zero input response • General nth-order differential equation • Zero-input response: x(t)=0 Homogeneous Equation • Solution of the Homogeneous Equation is the natural/general response/solution or complementary function Leo Lam © 2010-2012 19 Zero input response (example) • Using the first example: • Zero-input response: x(t)=0 • Need to solve: • Solve (challenge) Leo Lam © 2010-2012 n for “natural response” 20 Zero input response (example) • Solve • Guess solution: • Substitute: • One term must be 0: Characteristic Equation Leo Lam © 2010-2012 21 Zero input response (example) • Solve • Guess solution: • Substitute: • We found: • Solution: Unknown constants: Need initial conditions Leo Lam © 2010-2012 Characteristic roots = natural frequencies/ eigenvalues 22 Summary • Differential equation as LTI system • Complete example tomorrow Leo Lam © 2010-2012