* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture_3 - Department of Mathematics
Newton's laws of motion wikipedia , lookup
Gibbs paradox wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Entropy of mixing wikipedia , lookup
Thermal radiation wikipedia , lookup
Gibbs free energy wikipedia , lookup
Heat transfer physics wikipedia , lookup
Temperature wikipedia , lookup
Internal energy wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
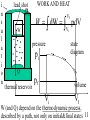
USSC2001 Energy Lecture 3 Thermodynamics of Heat Wayne M. Lawton Department of Mathematics National University of Singapore 2 Science Drive 2 Singapore 117543 Email [email protected] http://www.math.nus/~matwml Tel (65) 6874-2749 1 TUTORIAL 3 1. In problem 2, tutorial 2, (i) show that angles a1, a2 opposite sides with lengths 1m,2m are not determined but the ratio sin(a1)/sin(a2) is determined and compute it, (ii) let M denote the mass of the object on the side having length 2m and express the change of total gravitational potential energy if the system has a ‘virtual displacement’ in which the object with mass M moves by distance d downwards, (iii) explain the “Principle of Virtual Work” and use it to compute the value of M if the system is in equilibrium, (iv) discuss Simon Stevinus and use his method to compute M. http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Stevin.html http://3quarksdaily.blogs.com/3quarksdaily/2005/05/monday_musing_s.html 2 WHAT IS THERMODYNAMICS? Read chapter 19 (handouts) of Halliday, Resnick and Walker, study Review&Summary and Problems. Deals with thermal (internal) energy and involves the concept of temperature, an elusive property of objects that alters apparent properties, including lengths & volumes and electrical resistance, any of which can be used to make a thermoscope (not yet a thermometer). Zeroth Law of Thermodynamics: If bodies A and B are each in thermal equilibrium with a third body T, then they are in thermal equilibrium with each other. 3 DEFINING TEMPERATURE The triple point of water http://en.wikipedia.org/wiki/Triple_point 273.16 K degrees Kelvin 611.73 Pa Pascals We define the temperature of a gas by p(T ) T 273.16 K lim gas0,vol const p ( 273.16 K ) Here we use the fact that T is the same for ALL gases. 4 CONSTANT-VOLUME GAS THERMOMETER The ingenius mercury thermometer shown below (page 428 in HRW) can measure T at constant volume p atm 1.01 10 Pa 3 3 mercury 13.6 10 kg / m 5 Questions How is constant volume maintained at different temperatures? How is density measured? p T Gasfilled bulb h p patm gh Reservoir that can be raised and lowered 5 TEMPERATURE SCALES All scales are inter-related by affine functions f(x) ax b, a, b { Real Numbers } And therefore determined by their values at absolute zero and the triple point of water Absolute zero 0K 273.15 C 459.67 F Triple point 273.16 K 0.01 C 32 .02 F Question Compute the values of a and b for the six affine functions that convert K C, K F, C K, C F, F K, F C 6 IDEAL GAS LAW Amadeo Avogado 1776-1856 suggested that all gases contained the same number of molecules for a fixed volume, pressure and temperature pV kT molecules = where N A 6.02 10 32 k 1.38 10 23 pV RT moles = # molecules in a mole J / K = the Boltzmann constant R 8.314 joules / (mole K) = the gas constant Question How are k and R related? 7 TUTORIAL 3 2. Newton’s 3rd Law states: When 2 bodies (particles) interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction. The (linear) momentum of a body is defined to be the product of its mass times its velocity and the momentum of a system is the ‘sum of its parts’ (i) use Newton’s laws to show that when 2 bodies interact (eg in a collision) the system momentum is conserved, (ii) compute the average pressure that a molecule with kinetic energy E_kin exerts on a cubic container with volume V, (iii) combine this and the ideal gas law to show average molecular kinetic energy = 3kT/2 8 TEMPERATURE AND HEAT Thermal or internal energy consists of kinetic and energies associated with their random motions and, especially for solids and liquids, the potential energy due to their proximity. Heat Q is thermal energy transferred to a system from its environment, Q > 0, Q < 0 when the system temperature is lower, higher than environment’s, it can be associated with a change of temperature Q cm(Tf Ti ) where m=mass and c = specific heat capacity of a material (c=4190J/(kg K for water at 14.5C) or with a change of phase (heats of fusion and vaporization). 9 HEAT TRANSFER MECHANISMS Heat can be transferred by conduction dH Thot Tcold kA dt L convection, and radiation dH 4 4 A(Tenv T ) dt Questions What are the constants in these equations? 10 i n s u l a t i o n lead shot pi W WORK AND HEAT Vf W dW pdV Vi pressure pi state diagram Q thermal reservoir pf volume Vi Vf W (and Q) depend on the thermodynamic process, described by a path, not only on initial&final states 11 THERMODYNAMIC PROCESSES As shown on p 438-439 in HRW, W = the work done by a system is path dependent, this is also true for Q = heat transferred to the system since, as stated in lines 6-8 from bottom page 435 that gases have different values for their specific heats under constant-pressure and under constant-volume conditions. Question Compute W for constant p and constant T Vf W p const pdV p (Vf Vi ) Vi Vf nRT Vf WT const dV nRT ln Vi V Vi 12 FIRST LAW OF THERMODYNAMICS There exists an internal energy function E int E int (V , p) such that during any thermodynamic process E int Q - W The first law is illustrated for adiabatic (Q=0), constant volume (W = 0), and closed cycle or cyclic processes on page 441 of HRW. Free expansion on page 442 differs from all other processes why? 13 SECOND LAW OF THERMODYNAMICS There exists an entropy function S S (V , p ) such that during any thermodynamic process S Sf - Si (Vf , p f ) (Vi , p i ) dQ T or, equivalently, such that Sf Q T dS Si 14 TUTORIAL 3 3. Combine the formular dE int dQ - dW with the ideal gas law and the eqn. dE n C dT int V where n moles of a quantity of gas and CV molar specific heat at constant volume to show that for an ideal gas Vf Tf S Sf - Si n R ln n CV ln Vi Ti 4. Find out what a Carnot Cycle is and how it differs from a Stirling Cycle. What is more efficient? 5. What is free energy and how does it explain 15 the thermodynamics of chemical reactions?