Download Document

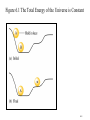
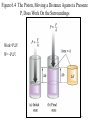
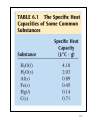
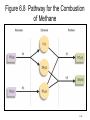
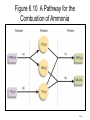
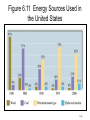
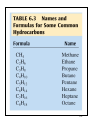
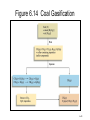
Ch. 6 Thermochemistry
• The relationship between chemistry and energy
•Basic concept of thermodynamics
•Energy conversion:
Energy: the capacity to do work or to produce heat
Law of conservation of energy: energy can be converted from
one form to another but can be neither created nor destroyed.
6–1
Basic concepts of thermochemistry
Energy is classified as:
Potential energy: energy due to position or composition
Kinetic energy: energy due to the motion of an object
KE = ½ mv2
6–2
Figure 6.1 The Total Energy of the Universe is Constant
6–3
Basic concepts of thermochemistry
Two ways of the energy transfer:
Heat: energy transferred between two objects due to a temperature
difference between them.
Work: force acting over a distance (w = f x d)
Ex. Gas expansion and compression
F
P=
A
Work = force x distance = F x Δh
Since P = F/A or F = P x A, then
Work = P x A x Δh
For a cylinder device, ΔV= finial volume – initial volume = A x Δh
Then, Work = P x A x Δh = PΔV
6–4
Figure 6.4 The Piston, Moving a Distance Against a Pressure
P, Does Work On the Surroundings
Work=PΔV
W= -PΔV
6–5
Figure 6.2 Exothermic Process
(Energy flows out of the system)
The energy gained by the
surroundings must be equal to
the energy lost by the system.
In any exothermic reaction, some of the potential energy stored in
the chemical bonds is being converted to the thermal energy via heat.
6–6
System: the object being studied at a given moment.
a macroscopic system
a closed system
an open system
an adiabatic system
an isolated system
Surroundings: The portion of universe that is outside the system.
6–7
Figure 6.3 Endothermic Process
(heat flow is into the system)
6–8
Basic concepts of thermochemistry
Unit of energy:
SI unit of energy: joule =
Kg m 2
S2
KE = ½ (mv2) =1/2 x 2.0Kg (1m/s)2 (if m = 2.0 Kg and v = 1 m/s)
= 1.0
Kgm2
S2
= 1.0 joule
1 Calorie = the heat required to raise the temperature of 1.00 g
pure water 1.00C (from 14.5 to 15.50C)
1 cal = 4.184 joules
1Kcal = 1000 calories
6–9
heat absorbed
Heat capacity C =
increase in temperature
∴ q = CΔT
Specific heat capacity (s) : the heat capacity is given per gram
of substance. (J/oC·g or J/K·g)
Molar heat capacity : the heat capacity is given per mole of
substance. (J/oC·mol or J/K·mol)
= s/ molar mass
Using specific heat capacity: energy exchanged = C· m · T
ex.
6–10
6–11
Figure 6.5
A CoffeeCup
Calorimeter
Made of
Two
Styrofoam
Cups
6–12
Thermodynamics: the study of energy and its interconversions.
Thermochemistry: the relationship between chemical reaction and
energy change.
The 1st law of thermodynamics: the energy of universe is constant.
(能量守恆定律)
The internal energy (E) of a system is the sum of KE and PE of all
particles in the system. The internal energy of a system can be
changed by a flow of work, heat, or both. i.e.
ΔE = q + w ΔE: change of E, q: heat, w: work
Thermodynamic quantities always consist of two parts:
a number, giving the magnitude of the change
a sign, indicating the direction of the flow
Ex. A quantity of energy flows into the system via heat (an
endothermic process), +x, and -x for an exothermic process.
6–13
Ex 6.1, 6.2, 6.3
6–14
Figure 6.4 The Piston, Moving a Distance Against a Pressure
P, Does Work On the Surroundings
w =PΔV
w = -PΔV
ΔV > 0, expansion → w < 0, system does work to the
surroundings
ΔV < 0, compression → w > 0, work has done on the system6–15
QUESTION 1
The combustion of a fuel is an exothermic process.
This means…
1. the surroundings have lost exactly the amount of
energy gained by the system.
2. the potential energy of the chemical bonds in the
products should be less than the potential energy
of the chemical bonds in the reactants.
3. q must be positive; w must be negative
4. E would have a + overall value because the
surroundings have gained energy.
6–16
QUESTION 2
A gas absorbs 0.0 J of heat and then
performs 15.2 J of work. The change in
internal energy of the gas is:
1) –24.8 J.
2) 14.8 J.
3) 55.2 J.
4) –15.2 J.
5) none of these.
6–17
QUESTION 3
Which of the following statements is correct?
1) The internal energy of a system increases when
more work is done by the system than heat was
flowing into the system.
2) The internal energy of a system decreases when
work is done on the system and heat is flowing into
the system.
3) The system does work on the surroundings when an
ideal gas expands against a constant external
pressure.
4) All statements are true.
6–18
State function: A property of a system that is determined by the
state of condition of the system and not by the how it got to the
state; its value is fixed when temperature, pressure, composition,
and physical form are specified; P, V, T, E, and H are state
functions. Because E is a state function, ΔE depends only on the
initial and finial states of the system and not how the change
occurs.
Ex. of textbook:
Denver (elevation 5180 ft) , Chicago (elevation 674 ft)
Δh = 5280-674 = 4606 ft
Elevation is a state function and distance is not.
State function: A quantity whose changed value is determined only
by its initial and finial vales.
6–19
Figure 6.6 A Bomb Calorimeter.
(constant volume)
E = q + w
=q
= qv
6–20
Figure 6.6
A Bomb
Calorimeter
6–21
•Heat transfer at const. V: Bomb calorimeter
ΔE = qv
•Heat transfer at const. P : Enthalpy
ΔE = qp + w = qp –PextΔV
ΔE = qp –PΔV, (Pext = Pinternal = Psystem)
qp = ΔE + PΔV ;
PΔV= Δ(PV) for const. P
qp = Δ(E + PV)
Enthalpy (焓)
H = E + PV
 qp = Δ(E + PV) = ΔH
ΔH = qp = ΔE + PΔV
(only at constant pressure)
∵ E, P, and V are state functions; H is a state function
•The enthalpy changed,  H, is the heat added to (or lost by) a
system.
•For a chemical reaction, the enthalpy change is:
 H = Hproducts - Hreactants
6–22
A Group of Firewalkers in Japan
6–23
Thermochemistry
Energy:
1. kinetic energy
2. potential energy
3. internal energy (E)
E: Total energy of the system;
due to K.E.
due to P.E.
due to chemical energy stored in chemical bond: thermochemistry
Reaction enthalpies:
qreaction (at cont. P) = ΔH = Hproducts – Hreactants
ΔH > 0; endothermic reaction
ΔH < 0; exothermic reaction
1
CO(g) + O2 (g) → CO2 (g)
2
1
CO2 (g) →
CO(g) + 2 O2 (g)
2CO2 (g) →
2 CO(g) + O2 (g)
ΔH = -283.0 kJ
ΔH = +283.0 kJ
ΔH = +566.0 kJ
Hess’s Law
6–25
Hess’s Law
C(s) + O2 (g) → CO2 (g)
ΔH = -393.5 kJ
CO2 (g) → CO(g) + 1 O2 (g)
ΔH = +283.0 kJ
2
-------------------------------------------------------------------1
C(s) +
O2 (g) → CO(g)
ΔH = ?
2
equation = equation (1) + equation (2) +
ΔH = ΔH1 + ΔH2 + 
Note:
•
The sign of ΔH indicates whether the reaction is endothermic
or exothermic reaction.
•
ΔH change sign when a reaction is reversed.
•
The magnitude of ΔH is directly proportional to the quantities
of reactants and products, the coefficients represent number of
mole. (ΔH  amount of reactants or products)
•
The phases (physical states) of all species must be specified,
using the symbol of (s), (l), and (g).
H2O(s) → H2O(l)
H2O(l) → H2O(s)
ΔHfus = -ΔHfreez
ΔHfus = +6.007 kJ mol-1
ΔHfreez = -6.007 kJ mol-1
Given
H2 (g) +
1
2
O2 (g) → H2O (l)
Calculate ΔH for the equation
2H2O (l) → 2H2 (g) + O2 (g)
ΔH = -285.8 kJ
ΔH = ?
Graphite
6–28
Standard-State Enthalpies (ΔHo)
•Absolute Energies and absolute enthalpies cannot be measured and
calculated. Only ΔH and Δ , sometime, the measurement of ΔH is
impossible, ΔH can be obtained by cal E can be measured.
Standard-States for chemical substances:
For compounds
•For pure solids and liquids (condensed states), pure liquid or solid
at 1 atm and specified temp (298.15 oK)
•For gases, 1 atm and specified temp.
•For dissolved species, 1 M solution at 1 atm and specified temp.
For elements
•The standard states of elements are the forms which the elements
exit under conditions of 1 atm and 25oC.
The standard state for oxygen is O2(g); the standard state for
sodium is Na(s); the standard state for mercury is Hg(l); etc.
Standard enthalpy of formation (ΔHfo)
•def: The enthalpy change for the reaction that produces one mole of
the compound from its elements in their stable states.
.
1
H2 (g) +
O2 (g) → H2O (l)
ΔH = -285.83 kJ
2
o
ΔHf (H2 O(l)) = -285.83 kJ mol-1
1
ΔH = +217.96 kJ
2 H2 (g) → H(g)

ΔHfo(H (g)) = +217.96 kJmol-1
Table 6.2 Standard Enthalpies of Formation for
Several Compounds at 25°C
6–31
Figure 6.8 Pathway for the Combustion
of Methane
6–32
Figure 6.9 Schematic Diagram of
Energy Changes
6–33
Figure 6.10 A Pathway for the
Combustion of Ammonia
6–34
Figure 6.11 Energy Sources Used in
the United States
6–35
6–36
6–37
6–38
Figure 6.12
The
Atmosphere
Traps Some
Light Energy,
Keeping the
Earth Warmer
than it
Otherwise
Would Be
6–39
Figure 6.14 Coal Gasification
6–40