Download Ultrathin Films and Some Cross Effect

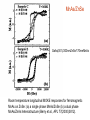
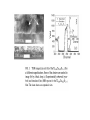
Amorphous films, Magneto-optical films and
magnetic simeconductor films
(1) Amorphous films
(2) magneto-optical effect and Materials
(3) dilute semiconductor
Preparation of amorphous films
Rapid cooling via Vacuum evaporation, Sputtering
Many elements (ribbons FeNiPB, FeCoSiB, CoSiB….)
Size difference (GdCo, TbFe, YFe….)
Cooling the substrate
Characters: x-ray, conductivity, phase transition……
Chaudhari et al., APL(1973)202
Tc increases with the increasing Co content
Tc decreases from Gd, Tb, Dy, Ho……
Mean Field Theory
GdCoMo
Single ion model
Moorjani and Coey Magnetic glasses p201
Suzuki et al., JAP 83(1988)3633
Shang and Wang et al PRL 63(1989)449; Wang and Kleemann PRB 44(1991)5132
Wang and Kleemann PRB 44(1991)5132
y
Atom pair model
θ2
M
2
θ1
r
12
x
M1
(a)
(b)
The potential energy of the system is
U= - (1/2)(M1xH1x+M1yH1y+ M2xH2x+M2yH2y)
= - (M1M2/4πμor123) (2cosθ1cosθ2 - sinθ1sinθ2)
If the two dipoles have the same magnetic moment, M1=M2=M and if
they are always parallel to each other, that is θ1=θ2=θ, the above
expression because
U= - [ 3M2/(4πμor123) ](cos2θ-1/3)
In the general case the potential energy is given by
U = (1/(4πμor123)) [(M1•M2) - 3/r2 (M1•r)( M2•r)]
The total dipolar energy for AA, BB and AB pairs can be expressed in
terms of probability functions PAA (r ), PBB (r ), and PAB (r ) . The average dipolar
energy associated with AA pairs, per A atom, is given by
The anisotropic probability functions may be expressed using spherical
harmonics as follows
N total number of atoms per unit volume, Nj the number of j type
anisotropy in alignment of ij atom pair
Cargill et al., JAP 49(1978)1753, 50(1979)3570
PRL 66(1991)1086, 69(1992)1939, 87(2001)067207 Pair model
Gd0.11Co0.67Mo0.16Ar0.06
Tb0.26Fe0.74 amorphous film
Harris et al., PRL 69(1992)1939
Magneto-optical Effect
1876 John Kerr
The three types of geometries of the Kerr effect
Magneto-optical Effect
θ k is defined as the main polarization plans is tilted over
a small angle;
εk = arctan(b/a).
Definition
The arrangement of the magnetization M and wave vector
k in the local coordination employed in the derivation of the pMOKE equation for Normal incidence.
The dielectric tensor has the following form
(1)
The normal model solution to the Fresnel Eq.
(2)
and the corresponding electric field model are
(3)
The definition of Kerr rotation and
Kerr ellipticity
Kerr rotation and ellipticity are expressed by the
component of conductivity sensor
θk = -Im [(n+ -n-)/( n+n- -1)]
εk = -Re[(n+ -n-)/( n+n- -1)]
n+ = n+ -ik+, n- = n- -ik-
r+ - =(n+ - -1)/( n+- +1)
Kittel Introduction to solid state physics, chapter 11: optical process and excitons
E (refl) / E (inc) = r(ω) = ρ(ω)exp[iθ(ω)]
r(ω) = (n+ik-1)/(n+ik+1)
R = E*(refl)E(refl)/E*(inc)E(inc) = r*r = ρ2
ε(ω)1/2 = n(ω) + ik(ω)
Once we know both R(ω) and θ(ω), we can obtain
n(ω) and k(ω),
then to getε(ω)= ε’(ω) +iε’’(ω)
The off-diagonal terms σxy are proportional to M and describe the MOKE.
Both diagonal and off-diagonal terms are complex quantities,
σij =σ1ij +i σ2ij
The absorptive component of diagonal terms σ1xx is proportional to the sum
of absorption of left and right circularly polarized light (RCP and LCP).
the absorptive component off-diagonal term σ2xy is proportional to the difference
in absorption of LCP and RCP components.
Erskine and Stern PRB 12(1975)5016
微观理论
在铁磁性金属物质中的磁光效应源于带内(intraband)和带间(interband)电子跃迁。前者局限于
低能量端的跃迁，而后者发生在高能量区，常见的在可见光范围。磁光效应与电导张量非对角元密
切相关。微观上，这一非对角元由自旋取向向上和向下两部分各自的跃迁之和来表示。
σ2xy=σ2xy↑(ω)+ σ2xy↓(ω)
在自旋向上或向下的各自的初终态α和β之间的跃迁贡献为
σ2xy=(2πe2/4hm2Vω) Σαβ[(|<β↑|π-|α↑>|)2 + (|<β↓|π-|α↓>|)2
-(|<β↑|π+|α↑>|)2 - (|<β↓|π+|α↓>|)2 ] δ(ωαβ –ω)
(5-10)
这里, π± =πx ±iπy 为运动量矩算符，定义为：π=p(h/8πmc2)S×▽V(r), p是动量矩算符，
S×▽V( r )描写自旋轨道耦合，v为总的体积,
h ωαβ =εβ -εα
显然,式5-10可视为一个光子的吸收过程，即一个电子从初态占有初态α到非占有终态β间的跃迁。
δ(ωαβ-ω) 表示为跃迁过程中的能量守恒.矩阵元(α|π+|β)和(α|π-|β)相应于右园和左园偏振
的跃迁.因此σ2xy比例于右园和左园偏振光吸收概率之差.从理论计算可以推得σ1xx (ω) 比例于平
均吸收,非对角元色散部分σ2xx (ω)和σ1xy (ω)可以通过Kramers关系推得.
上述跃迁必需满足Δl=±1, Δml =±1
第一选择定则表明，跃迁只能发生在s和p能级间或p和d能间间，第二选择定则表明，右园和左园偏
振跃迁需分别满足Δml =-1和Δml =+1.
Double Layers
±
rⅠ± rⅡ
MO layer
Reflector
Reim and Weller IEEE Trans on Mag., 25(1989(3752
Faraday Effect
Bennett and Stern PR 137(1965)A448
Petros N. Argyres, Theory of the Faraday and Kerr effect in ferromagnets, PR 97
(1955)334,
P.M. Oppeneer, Magneto-optical Kerr spectra in Handerbook of Magnetic Materials,
Edited by Buschow (Vol.13), Physical Review B, 45(1992)10924.
From Oppeneer Magneto-optical Kerr spectra in Hanbook of magnetic
Materials, Edited by Buschow (Vol.13)
Experimental pola Kerr ritation an undoped MnBi sample (Di et al. 1992)
and Al-doped MnBi sample at room ) temperature (Shang et al., 1997).
Diluted Magnetic Semiconductors
• The charge of electrons in Semiconductor
(Integrated circuits, devices);
• Spin of electrons in data storage (hard
disc, tapes, magneto-optical disks)
May we be able to use the capability of mass storage and
processing of information at the same time ?
If both the charge and spin of electrons can be used to further
enhance the performance of devices.
Three types of semiconductors: (A) a magnetic semiconductor, (B)
a diluted magnetic semiconductor, an alloy between nonmagnetic
semiconductor and magnetic element; and (c) a nonmagnetic semiconductor.
wide band gap Ⅲ-Ⅴ,Ⅱ-Ⅵ as host
Mn(Fe)GaAs
Co(Fe,Ni,V,Cr)+Ti02(ZnO)
MnAs/ZnSe
Others (ZnMnO)
For most doped DMS Tc<room temperature
Co-Ti02 Tc ～400K
ZnMnO room T
GaMnAs
Lattice constant a vs Mn composition x in (Ga1-x, Mnx)As films.
a was determined by XRD at room temperature (Ohno et al.,
APL 69(1996)363.
Magnetic field dependence of magnetization M at 5K for a
(Ga, Mn)As film with xMn=0.035. The field was applied parallel
to the sample surface (Ohno et al., APL 69(1996)363).
MnAs/ZnSe
GaAs(001)/200nmZnSe/170nmMnAs
Room temperature longitudinal MOKE responses for ferromagnetic
MnAs on ZnSe: (a) a single phase MnAs/ZnSe (b) a dual phase
MnAs/ZnAs heterostructure (Berry et al., APL 77(2000)3812).
ZnCoAl
XRD patterns and VSM curves of the thin films
deposited at 400 oC at oxygen pressure 5x10-5 Pa
(Yan et al., JAP 96(2004)508).
Co doped TiO2
Matsumoto et al., Science 291(2001)854
Atomic resolution TEM image. No
An XRD pattern of a Co doped TiO2 film
segregation of impurity phase was
(x=0.08) showing (004) and (008) peaks
observed.
of anatase(锐钛矿) without any impurity peaks.
A series of scanning SQUID microscope images
200 µm x 200 µm
Images taken at 3K for anatase thin films with different Co contents on a
combinatorial chip. (a) x=0, (b) 0.02, (c) 0.03, (d) 0.06. Magnetic domain
were observed in all doped film.
(a) an M-H curve of an x=0.07 film on SrTiO3 taken at room temperature.
(b) M-T curve in a field of 20 mT parallel to the surface. Tc > 400K.
PRL 90(2003)017401
Ti0.99Co0.01O2-δ
Small Clusters of Co results in Ferromagnetism in Co doped TiO2 (金红石)
APL 86(2005)222503
Co 2+ or Co clusters
Zn1-xMnxO
Source ?
(1) Zener Model
(2) RKKY interaction (H.Ohno Science 281(1998)951);
(3) Forming resonant states (J.Inoue et al., PRL 85(2000)
4610;
(4) Clusters of Co in Co-doped anatase TiO2 thin film (J.K.
Kim et al., PRL 90(2003)017401.
Science 287(2000)1019
Driven by exchange
Between carriers and
Localized spin
(PR 81(1950)440)
Fig. Normalized ferromagnetic temperature as a function of
Hole concentrations
Tc is determined by Eq.(2)
Tc(x) = Tcnor (F)(x) - Tc (AF) (x)
AF is Fermi parameter, xeff is the effective spin magnitude,
β is p(carriers)-d exchange integral, No is the concentration of the cation sites,
Tc = TF – TAF, TFnor is normalized ferromagnetic temperature
Fig.2, Curie temperature Tc in Zn1-xMnxTeN for various Mn contents x and hole concentrations
ρ deduced from the Hall resistance at 300 K. Theoretical predictions areindicated by the red mesh.
RKKY
(Mn1-x Gax)As 200nm thick
B (T)
(F.Matsukura et al., PRB 57(1998)R2037)
(Mn1-x Gax)As