Download 6. - Kent

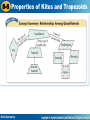
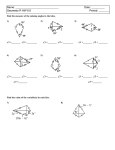
Conditions for Special Parallelograms
Entry Task
• List the 6 ways to prove a quadrilateral is a
parallelogram, show a picture of each.
for Special Parallelograms
IsConditions
it a
parallelogram??
Rhombus
• 4 congruent sides
• Diagonals that
Rectangle
bisect opp.
• 4 rt. Angles
Angles
• Congruent diagonals • Perpendicular
diagonals
Square
(must have 1 property from rectangle and rhombus)
• 4 congruent sides
• 4 rt. Angles
• Diagonals that
bisect opp. Angles
• Congruent diagonals
• Perpendicular
diagonals
6-6 Properties of Kites and Trapezoids
Learning targets
I know and understand the properties of
trapezoids and kites
Success Criteria
I can use properties of kites and trapezoids to
solve problems.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Vocabulary
kite
trapezoid
base of a trapezoid
leg of a trapezoid
base angle of a trapezoid
isosceles trapezoid
midsegment of a trapezoid
Holt Geometry
6-6 Properties of Kites and Trapezoids
A kite is a quadrilateral with exactly two pairs of
congruent consecutive sides.
Holt Geometry
6-6 Properties of Kites and Trapezoids
*Note – These are NOT parallelograms!
Holt Geometry
6-6 Properties of Kites and Trapezoids
A trapezoid is a quadrilateral with exactly one pair of
parallel sides. Each of the parallel sides is called a
base. The nonparallel sides are called legs. Base
angles of a trapezoid are two consecutive angles
whose common side is a base.
If the legs of a trapezoid are
congruent, the trapezoid is
an isosceles trapezoid.
The following theorems
state the properties of an
isosceles trapezoid.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Holt Geometry
6-6 Properties of Kites and Trapezoids
The midsegment of a trapezoid is the segment
whose endpoints are the midpoints of the legs. In
Lesson 5-1, you studied the Triangle Midsegment
Theorem. The Trapezoid Midsegment Theorem is
similar to it.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Check It Out! Example 2c
In kite PQRS, mPQR = 78°,
and mTRS = 59°. Find each
mPSR.
mSPT + mTRS + mRSP = 180° Polygon  Sum Thm.
mSPT = mTRS
Def. of  s
mTRS + mTRS + mRSP = 180° Substitute.
59° + 59° + mRSP = 180° Substitute.
Simplify.
mRSP = 62°
Holt Geometry
6-6 Properties of Kites and Trapezoids
1. Erin is making a kite based on
the pattern below. About how
much binding does Erin need to
cover the edges of the kite?
about 191.2 in.
In kite HJKL, mKLP = 72°,
and mHJP = 49.5°. Find each
measure.
2. mLHJ
Holt Geometry
81°
3. mPKL
18°
6-6 Properties of Kites and Trapezoids
Example 3A: Using Properties of Isosceles
Trapezoids
Find mA.
mC + mB = 180°
100 + mB = 180
Holt Geometry
Same-Side Int. s Thm.
Substitute 100 for mC.
mB = 80°
A  B
Subtract 100 from both sides.
Isos. trap. s base 
mA = mB
Def. of  s
mA = 80°
Substitute 80 for mB
6-6 Properties of Kites and Trapezoids
Example 5: Finding Lengths Using Midsegments
Find EF.
Trap. Midsegment Thm.
Substitute the given values.
EF = 10.75
Holt Geometry
Solve.
6-6 Properties of Kites and Trapezoids
Check It Out! Example 5
Find EH.
Trap. Midsegment Thm.
1
16.5 = 2 (25 + EH) Substitute the given values.
Simplify.
33 = 25 + EH
Multiply both sides by 2.
13 = EH
Subtract 25 from both sides.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Holt Geometry
6-6 Properties of Kites and Trapezoids
Homework
p. 394 #7-23 odds, 26 and 29-35 odds,47-52
Challenge - 63
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 1: Problem-Solving Application
Lucy is framing a kite with
wooden dowels. She uses two
dowels that measure 18 cm,
one dowel that measures 30
cm, and two dowels that
measure 27 cm. To complete
the kite, she needs a dowel to
place along . She has a dowel
that is 36 cm long. About how
much wood will she have left
after cutting the last dowel?
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 1 Continued
1
Understand the Problem
The answer will be the amount of wood Lucy has
left after cutting the dowel.
2
Make a Plan
The diagonals of a kite are perpendicular, so the
four triangles are right triangles. Let N represent the
intersection of the diagonals. Use the Pythagorean
Theorem and the properties of kites to find ,
and
. Add these lengths to find the length of
.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 1 Continued
3
Solve
N bisects JM.
Pythagorean Thm.
Pythagorean Thm.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 1 Continued
Lucy needs to cut the dowel to be 32.4 cm long.
The amount of wood that will remain after the
cut is,
36 – 32.4  3.6 cm
Lucy will have 3.6 cm of wood left over after the
cut.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 1 Continued
4
Look Back
To estimate the length of the diagonal, change the
side length into decimals and round.
, and
. The length of the diagonal is
approximately 10 + 22 = 32. So the wood
remaining is approximately 36 – 32 = 4. So 3.6 is a
reasonable answer.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 4B: Applying Conditions for Isosceles
Trapezoids
AD = 12x – 11, and BC = 9x – 2. Find
the value of x so that ABCD is
isosceles.
Diags.   isosc. trap.
AD = BC
Def. of  segs.
Substitute 12x – 11 for AD and
12x – 11 = 9x – 2 9x – 2 for BC.
3x = 9
x=3
Holt Geometry
Subtract 9x from both sides and add
11 to both sides.
Divide both sides by 3.
6-6 Properties of Kites and Trapezoids
Check It Out! Example 4
Find the value of x so that
PQST is isosceles.
Q  S
mQ = mS
Trap. with pair base
s   isosc. trap.
Def. of  s
2 + 19 for mQ
Substitute
2x
2x2 + 19 = 4x2 – 13 and 4x2 – 13 for mS.
32 = 2x2
x = 4 or x = –4
Holt Geometry
Subtract 2x2 and add
13 to both sides.
Divide by 2 and simplify.
6-6 Properties of Kites and Trapezoids
Example 3B: Using Properties of Isosceles
Trapezoids
KB = 21.9m and MF = 32.7.
Find FB.
Isos.  trap. s base 
KJ = FM
Def. of  segs.
KJ = 32.7 Substitute 32.7 for FM.
KB + BJ = KJ
Seg. Add. Post.
21.9 + BJ = 32.7 Substitute 21.9 for KB and 32.7 for KJ.
BJ = 10.8 Subtract 21.9 from both sides.
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 3B Continued
Same line.
KFJ  MJF
Isos. trap.  s base 
Isos. trap.  legs 
∆FKJ  ∆JMF
SAS
BKF  BMJ
CPCTC
FBK  JBM
Vert. s 
Holt Geometry
6-6 Properties of Kites and Trapezoids
Example 3B Continued
Isos. trap.  legs 
∆FBK  ∆JBM
AAS
CPCTC
Holt Geometry
FB = JB
Def. of  segs.
FB = 10.8
Substitute 10.8 for JB.
6-6 Properties of Kites and Trapezoids
Lesson Quiz: Part II
Use the diagram for Items 4 and 5.
4. mWZY = 61°. Find mWXY.
119°
5. XV = 4.6, and WY = 14.2. Find VZ.
9.6
6. Find LP.
18
Holt Geometry