Download Scholarship Geometry Notes 6-6 Properties of Kites and Trapezoids

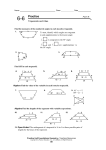
Scholarship Geometry Notes
6-6 Properties of Kites and Trapezoids
In this section we will look at two special quadrilaterals that are not parallelograms.
A kite is a quadrilateral that has 2 pairs of consecutive sides ≅.
There are three special properties.
1) ONE pair of opposite angles congruent (where the different length sides meet)
2) Diagonals are perpendicular.
3) ONE diagonal bisects the non-congruent angles AND the other diagonal.
Let’s mark the sketches.
Ex. 1: In kite ABCD, m∠DAB = 54° and m∠CDF = 52°. Find each measure.
a) m∠BCD
b) m∠ABC
m∠CDF = m∠CBF = 52°
m∠BCD = 180− 52− 52 = 76°
1
1
m∠BAF = m∠DAB = (54°) = 27°
2
2
m∠ABF = 180 − 27 − 90 = 63°
m∠ABC = 63° + 52° = 115°
Ex. 2: Erin is making a kite based on the pattern below. About how much binding does Erin
need to cover the edges of the kite?
64 ÷ 2 = 32
132 + 32 2 = x 2
1193 = x 2
52 2 + 32 2 = y 2
x ≈ 34.5 3728 = y 2
y ≈ 61.1
Perimeter = 34.5 + 34.5 + 61.1+ 61.1 = 191.2 in
A trapezoid is a quadrilateral with EXACTLY one pair of parallel sides.
Trapezoids can be deceptive. All of these are trapezoids.
The midsegment of a trapezoid is the segment that connects the midpoints of the legs.
It has two properties.
1) It is parallel to each base.
2) Its length is half the sum of the lengths of the bases (the average of the bases).
Ex. 3: Find EF.
EF =
1
1
(13.5+ 8) = ( 21.5) = 10.75
2
2
Ex. 4: Find LP.
1
(28 + x )
2
2 ⋅ 23 = 28 + x
46 = 28 + x
x = 46 − 28 = 18
23 =
An isosceles trapezoid is one in which the legs are congruent.
It has two properties.
1) Both pairs of base angles are congruent.
2) Diagonals are congruent.
Ex. 5: KB = 21.9 m and MF = 32.7 m. Find FB.
KB = MB = 21.9
MF = FB + MB
32.7 = FB + 21.9
FB = 32.7− 21.9 = 10.8 m
Ex. 6: Find the value of a that makes PQRS isosceles.
a 2 + 27 = 2a 2 − 54
27 + 54 = 2a 2 − a 2
81 = a 2
a=9
A Venn diagram is a way to show how objects are related.
Let’s fill in the one below with all of our types of quadrilaterals.
Quadrilaterals
Parallelograms
Rectangles
Kites
Squares
Rhombuses
Trapezoids
Isosceles Trap.