* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Parallel, Perpendicular, and Oblique Lines
Cartesian coordinate system wikipedia , lookup
Projective plane wikipedia , lookup
Euclidean geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Duality (projective geometry) wikipedia , lookup
Contour line wikipedia , lookup
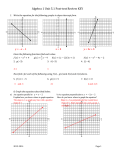
Parallel, Perpendicular, and Oblique Lines Using Coordinate Geometry to Find and Compare the Slopes of Lines Parallel Lines • Two lines are Parallel if they lie in the same plane and do not intersect Perpendicular Lines Two lines are Perpendicular if they intersect at a right (90°) Oblique Lines Two lines are Oblique if they lie in the same plane but are neither Perpendicular nor Parallel Skew Lines Two lines are Skew if they do not lie in the same plane Slope 𝑟𝑖𝑠𝑒 , 𝑟𝑢𝑛 Recall that slope = so draw in a slope triangle to find the rise and run l 3 6 4 8 𝑟𝑖𝑠𝑒 8 4 = = 𝑟𝑢𝑛 6 3 Parallel Lines Since Parallel lines never intersect but lie in the same plane, they must have the same slope l 3 3 4 4 m Slope of line l 𝑟𝑖𝑠𝑒 4 = = 𝑟𝑢𝑛 3 Slope of line m 𝑟𝑖𝑠𝑒 4 = = 𝑟𝑢𝑛 3 Perpendicular Lines Since Perpendicular lines intersect at right angles, there slopes are opposite reciprocals l 3 n 4 -3 4 Slope of line l 𝑟𝑖𝑠𝑒 4 = = 𝑟𝑢𝑛 3 Slope of line n 𝑟𝑖𝑠𝑒 −3 = = 𝑟𝑢𝑛 4 Oblique Lines Since Oblique lines are neither parallel nor perpendicular, there slopes are not equal, nor opposite reciprocals l 3 q 4 -3 7 Slope of line l 𝑟𝑖𝑠𝑒 4 = = 𝑟𝑢𝑛 3 Slope of line q 𝑟𝑖𝑠𝑒 −3 = = 𝑟𝑢𝑛 7 Review Parallel Lines Never intersect Same Slope Perpendicular Lines Intersect at a Right Angle Opposite Reciprocal Slope Oblique Lines intersect at a non-right angle Non-equal and non-opposite recriprocal slopes