Download Slides: RZC - Introduction

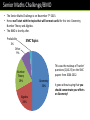
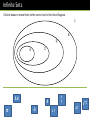
Topic 0: Introduction
Dr J Frost ([email protected])
Last modified: 12th September 2014
Slide Guidance
?

Any box with a ? can be clicked to reveal the answer (this
works particularly well with interactive whiteboards!).
Make sure you’re viewing the slides in slideshow mode.
For multiple choice questions (e.g. SMC), click your choice to
reveal the answer (try below!)
Question: The capital of Spain is:
A: London

B: Paris

C: Madrid

What and who this club is for
What we’ll concentrate on
•
•
•
•
•
Senior Maths Challenge
British Maths Olympiad
MAT
A little bit of STEP
Giving a general broad grounding
of maths to help with university
interviews, etc.
What this is not…
This is not intended to help you get
an A* at A Level or supplement the
content you do in your usual classes.
Much of what we’ll cover
(elementary number theory,
combinatorics, functional equations)
will likely be completely new topics
to you.
Who this is for
• People who enjoy maths who want to
explore the more interesting aspects
outside of the A Level curriculum.
• People who want to do well in the
SMC/BMO.
• People who are considering entry for a
maths-related degree at a competitive
university (particularly Oxbridge).
• I don’t presume people are doing Further
Maths.
Format/Admin
• Please ensure you put your name, email address and
school on the sign up sheet before you go.
• Please turn up on time!
• Most sessions you will be given a problem sheet to take
home with you. You’ll be emailed solutions the day
before the next session. It’s your responsibility to look
through these solutions; we won’t be going over them in
the sessions (although you’re welcome to ask me
questions on them)
• While these won’t be marked, please put as much effort
into them as possible – it doesn’t matter if you can’t
answer all the questions. ‘Doing problems’ is the most
effective way of appreciating the content we’ve covered.
To keep organised, you should put together a folder with dividers. Appropriate headings could be:
1. Geometry
2. Number Theory
3. Algebra
4. Combinatorics
5. Graphs
6. Prob/Stats
7. Functional Equations
8. Logic
9. Pigeonhole Principle
10. MAT
11. Other
Website
www.drfrostmaths.com/rzc
All slides, problem sheets, solutions and other supplementary materials will be put on
this website. Some topic slides will have an ‘Epilogue’ at the end: slides we won’t have
time to go through in these sessions, but are available for you to view online.
MAT
• This is the Oxford ‘Maths Admissions Test’.
• Up until 2013, was used exclusively by Oxford for those applying for Maths (and
joint courses) or Computer Science (and joint courses).
• Imperial College now use it for maths applicants.
• 2.5 hour (non-calculator) test. 40% of marks from multiple choice questions, 60%
from longer questions.
• Based on the C1 and C2 A Level Maths modules. But these aren’t just ‘harder A
Level questions’: they require a degree more ingenuity and dexterity.
• But it is the kind of test you can prepare for to some extent, and we’ll explore
some tips and theory useful for these papers later in the year.
• At Oxford, a mark of roughly 50% required to be invited to interview, and the
average mark of a successful applicant is about 75%.
British Maths Olympiad
• A 3 ½ hour paper consisting of just 6 questions.
• You’re invited to take it if you’re in roughly the top 1300 scorers in the Senior
Maths Challenge (in 2012, you needed a score of 93 out of 125 – this
corresponded to getting 17 out of 25 questions right)
• These questions are very difficult and the challenge is often knowing where to
start. Many of the questions however become more approachable if you’ve had
prior exposure to questions on a similar topic.
• Some questions are more ‘routine’ if you know the typical strategies. Others
require a novel idea that might not be obvious to think up.
• There’s a ‘Distinction’ award if you’re within the top 25% of people taking the test.
• The top 100 are awarded prizes, and most of these people are invited to ‘BMO
Round 2’. A small handful of these are subsequently selected for the national team
to compete in the International Maths Olympiad.
Senior Maths Challenge/BMO
• The Senior Maths Challenge is on November 7th 2013.
• Hence we’ll start with the topics that will be most useful for this test: Geometry,
Number Theory and Algebra.
• The BMO is shortly after.
Probability
2%
Other
9%
SMC Topics
Number
Theory
19%
Algebra
20%
This was the makeup of ‘harder’
questions (Q16-25) on the SMC
papers from 2004-2012.
Geometry
50%
It goes without saying that you
should concentrate your efforts
on Geometry!
STEP
•
•
•
•
•
This exam paper is used as an offer requirement for Cambridge and Warwick mathematics
courses. In contrast to MAT, you would take this in the summer of Year 13, not prior to your
university interview.
The paper is 3 hours. You have to choose 6 of the 13 questions (8 pure, 3 mechanics, 2
probability and statistics).
STEP paper questions are in some ways just ‘hard A Level questions’. But they differ in a few
ways:
• They are less guided than A Level questions. e.g. You might have to integrate by an
appropriate substitution: in an A Level exam they would give you the substitution, in a
STEP paper they wouldn’t.
• They require a good deal more technical dexterity – you can’t afford to be sloppy in your
maths.
Contrary to some people’s perceptions, STEP I, STEP II and STEP III are of comparable difficulty
(and indeed a similar distribution of people get the S, 1, 2 grades in each). It’s just that later
STEP papers are based on material later into the Maths/Further Maths A Level syllabus.
In contrast, MAT and BMO doesn’t really require any knowledge beyond C1 and C2.
Different exams
BMO
Difficulty
STEP
MAT
(This is a very rough
judgement!)
A Level
The extent to which the style of
question deviate from A Level ones.
Topics we’ll cover across the year
Geometry
Probability/Stats
Logic
Number Theory
e.g. If a throw a needle of length
𝑙 onto a board with horizontal
lines a distance of ℎ apart,
what’s the probability the
needle crosses a line?
e.g. What is the
maximum number of
the following
statements that can
be true? …
Functional Equations
MAT Prep
e.g. “How many multiples of
2013 have 2013 factors?”
Algebra
2
2
e.g. Prove that 𝑥 + 𝑦 ≥ 2𝑥𝑦
for all real 𝑥 and 𝑦.
e.g. Find all functions 𝑓 which
satisfy 𝑓 𝑥𝑦 = 𝑓 𝑥 + 𝑓(𝑦).
Pigeonhole Principle
Combinatorics
e.g. How many ways of pairing
2𝑛 people at a party?
Graph Sketching/Reasoning
e.g. Sketch 𝑦 = 2sin
2
𝑥
e.g. A cinema sells 31 tickets in
total one evening, and each
movie can be watched by up to
3 people. Show that the
minimum number of movies
seen by the same number of
people is 6.
Introduction
Set Notation
Here, we cover some basic set notation and common sets used to represent
collections of objects (usually numbers).
What is a set?
A set is a collection of items (often numbers) with two properties:
1. It can’t contain duplicates.
? doesn’t matter.
2. The order of the items
We can use curly braces to define a set, e.g. 1, −2, 4
By (2) above, 1, 2, 4 = {2, 4, 1}.
If a set has no items, it is known as the empty set, denoted by the symbol: ∅.
We say an item is a ‘member’ of a set if it is contained within the set.
If 𝑋 is a set, then:
means that 𝑥 is a member
? of 𝑋.
𝑥∈𝑋
2 ∈ 2,4
False

1 ∈ 1,2,3
False

True

True

(Click to vote!)
This is like asking “in a bag
containing balls labelled 1
and 2, do we have within this
bag another bag containing a
1?” No we don’t!
Infinite Sets
Some sets are infinite in size. Some are so common we use special symbols to represent
them:
Symbol
Name
ℕ
Natural numbers 1, 2, 3, 4, …
It’s not generally agreed whether 0 is
included. We could use ℕ0 if we
wanted to make explicit the 0 was
included, and ℕ+ to mean just ‘positive
numbers’ (which excludes 0).
?
ℤ
Integers 0, 1, −1,?2, −2, 3, −3, …
ℚ
Rational numbers
All numbers which can be expressed as
fractions 𝑝/𝑞, where 𝑝 and 𝑞 are
integers.
?
ℝ
Real numbers
?
Includes all numbers which can’t be
expressed as fractions.
ℂ
Complex numbers
?
Infinite Sets
Click to boxes to move them to the correct set in this Venn Diagram.
ℂ
ℝ
ℚ
ℤ
ℕ
3.4
𝝅
𝟔
𝟕
4
-3
𝟒. 𝟕
−𝟏
𝟓
Infinite Sets
Set notation is particularly useful when talking about functions:
𝑓 𝑥 = 𝑥 + 1 for all real 𝑥.
𝑓 𝑥 = 𝑥 + 1 for all 𝑥 ∈ ℝ.
?
𝑓 𝑥 = 𝑥 + 1, ∀ 𝑥 ∈ ℝ.
∀ means “for all”
Introduction
Proof
We look at what constitutes a ‘proof’, when a proof might be incomplete,
and the different types of proof often available.
When a proof is not a proof
Egbert claims that 𝑛2 + 𝑛 + 41 is prime for all integers 𝑛.
He tries it for 𝑛 from 1 to 39 and finds that the result is prime every
time.
How many values of 𝒏 would we need to try to show Egbert is wrong?
Just the one. This is known as a counterexample.
?
How many values of 𝒏 would we need to try to show Egbert is right?
Infinitely many, and clearly it wouldn’t be theoretically possible to show the
statement is true by exhaustively trying every 𝑛. We’d need some alternative
method.
Just trying 𝑛 = 1 𝑡𝑜 30 is not sufficient to prove the statement, and indeed,
the statement is false.
?
For example, mathematicians have found millions of pairs of primes which
differ by 2, which would at most ‘hint’ there’s infinitely many, but no one has
yet been able to formally ‘prove’ that there are infinitely many twin primes.
Counterexamples
Source: MAT
A

B

C
D

As we’ll see in the Logic topic later this year, the statement “If 𝐴, then 𝐵” is
only false when 𝐴 is true but 𝐵 is false.
What’s wrong with these proofs?
BMO1
Edwina:
Bob:
“Each row can have up to 4 counters in it. There’s 8 rows, so clearly
we can’t have more than 32 counters.”
She’s given an upper bound for the maximum (i.e. that the
maximum can’t be more than 32), but hasn’t actually shown we
give an arrangement of 32 counters?which satisfies the conditions.
For all we know, it’s not possible to do it with 32 counters.
Bob simply draws a valid arrangement using 32 counters
(and let’s say he’s right: the maximum is indeed 32 counters)
He hasn’t justified that we can’t have more than 32 counters.
This is easy to show, but needs to be?explicitly stated.
What’s wrong with these proofs?
BMO1
Dave:
Dave manages to (correctly) identify that that 𝒏 = 𝟏𝟏 works.
He hasn’t shown than 10 doesn’t work, i.e. that 11 is the smallest
?
𝑛.
Proof by contradiction
Proofs by contradiction are quite common in the BMO, so it’s always worth having at
the back of your mind to look out for sensible places to use it.
In general, to prove a statement by contradiction, we…
assume the statement is false, and show
? this leads to a contradiction.
So for this problem, to show 1, 2, … , 11 satisfies the condition given:
Assume it doesn’t satisfy the condition, i.e. that there exists a 𝑥, 𝑦, 𝑧, 𝑤 such that 𝑥 +
𝑦 + 𝑧 ≠ 𝑤. Show that this leads to a contradiction.
You could break the problem down by considering
whether the first few numbers are
?
the same or different colours, and then thinking what colouring the later numbers
must have to avoid satisfying the condition.
Proof by contradiction
BMO1
How would we use a proof by contradiction here?
Assume there was two distinct places to dig the treasure, 𝑥1 , 𝑦1 and 𝑥2 , 𝑦2 . Then
we’d need to show that in fact 𝑥1 = 𝑥2 , i.e. 𝑦1 = 𝑦2 , i.e. a contradiction, and thus
there is only one place to dig.
?
Doing so would involve forming 4 ‘Diophantine Equations’ (equations for which we’re
looking for integer solutions) which we’ll cover in the Number Theory topic.
Two-way proofs
BMO1
Sheila:
Sheila successfully manages to show that if 𝑨𝑪𝟐 = 𝑩𝑫𝟐 + 𝑪𝑬𝟐 , then
∠𝑨𝑩𝑪 = 𝟗𝟎°.
What’s wrong with her proof?
She only proved the statement in ‘one direction’. She didn’t prove that “if ∠𝐴𝐵𝐶 =
90° then 𝐴𝐶 2 = 𝐵𝐷2 + 𝐶𝐸 2 .
If we have the condition, “If 𝑋 is true then 𝑌 true”, then it’s quite possible that 𝑌 can be true
when 𝑋 is false, because the condition only cares about the case when 𝑋 is true, not when 𝑋 is
false.
?
But “If, and only if 𝑋 is true, is 𝑌 true” says something more. Suppose 𝑌 was true. Then unlike
above, 𝑋 can’t be false, because we said 𝑌 was true only if 𝑋 was true. Thus if 𝑌 is true, 𝑋 is true.
So:
Proofs needed:
X is true if, and only if, Y is true.
1. If X is true, then
𝑌 is true.
?
2. If 𝑌 is true, then 𝑋 is true.
Introduction
Epilogue: Proof by Induction
(‘Epilogue’ slides are not covered in class)
Proof by Induction
Further Mathematicians will do this soon enough in FP1, but for the benefit of those not
doing this A Level course, here’s a quick intro.
Suppose I wanted to show that some expression involving 𝑛 had some property for all
possible natural number values of 𝑛, e.g.
Prove that 8𝑛 − 3𝑛 is divisible by 5 for all 𝑛 ∈ ℕ
Clearly we can’t exhaustively check every value of 𝑛 up to infinity! But suppose we
showed that:
This is known as the
a. It’s true when 𝒏 = 𝟏
b. If it’s true for 𝒏 = 𝒌, then it’s true for 𝒏 = 𝒌 + 𝟏
base case.
This is known as the
inductive step.
If we’ve showed it’s true when 𝑛 = 1, then by (b), it’s also true for 𝑛 = 2. And if it’s true
for 𝑛 = 2, again by (b) it’s true for 𝑛 = 3. And hence we would have shown it’s true for
all natural numbers.
Proof by Induction
Prove that 8𝑛 − 3𝑛 is divisible by 5 for all 𝑛 ∈ ℕ
Base case:
When 𝑛 = 1, then 81 − 31 = 5 is divisible by 5.
?
Inductive step:
Assume the it’s true for 𝑛 = 𝑘. Then show it’s true for 𝑛 = 𝑘 + 1:
8𝑘+1 − 3𝑘+1
= 8 ⋅ 8𝑘 − 3 ⋅ 3𝑘
= 5 ⋅ 8𝑘 + 3 ⋅ 8𝑘 − 3 ⋅ 3𝑘
= 5 ⋅ 8𝑘 + 3?8𝑘 − 3𝑘
Clearly 5 ⋅ 8𝑘 is divisible by 5. And because we assumed the statement is true
for 𝑛 = 𝑘, 8𝑘 − 3𝑘 is divisible by 5 as well. So we’ve shown that if it’s true for
𝑛, it’s true for 𝑛 + 1.
Proof by Induction
There’s a slight variant of proof by induction which you WON’T see in FP1:
(there’s another good example in the Functional Equations slides)
a. It’s true when 𝒏 = 𝟏
b. If it’s true for 𝒏 = 𝒌, then it’s true for 𝒏 = 𝒌 + 𝟏
If it’s true for 𝒏 = 𝟏, 𝟐, 𝟑, … , 𝒌 then it’s true for 𝒏 = 𝒌 + 𝟏
Example:
Prove that every positive integer greater than one has at least 1 prime divisor.
Base case:
When 𝑛 = 2, then 2 itself is prime, and has itself as a prime divisor.
?
Inductive step:
Assume the it’s true for 𝑛 = 1, 2, 3, … , 𝑘.
If 𝑘 + 1 is prime, then it has itself as a prime divisor.
If it’s not prime, i.e. composite, then k + 1? = 𝑎𝑏 for some integers 𝑎 and 𝑏.
But 𝑎 ≤ 𝑘 and 𝑏 ≤ 𝑘. By induction, both are divisible by some prime divisor, say 𝑝1
and 𝑝2 . Then 𝑘 + 1 will be divisible by 𝑝1 and 𝑝2 .