Download Multi-Objective & Multi-Mode Assignment and Scheduling problem

Multi-objective and Multi-mode
Assignment and Scheduling Problem for
large volume Surveillance
Olfa Dridi
Saoussen Krichen
Adel Guitouni
Salamanca, Spain, 19-30 September
Outline
1.
Scheduling Theory
2.
Areas of Application
3.
Problem Description
4.
Literature Review
5.
6.
7.
Proposed Model
8.
9.
Multi-criteria Genetic approach
A bi-level ASP
Integration in Inform Lab
Conclusion
1. Scheduling Theory
• The project scheduling and resource management dates
from five hundred years: The Egyptian pyramids, the Great
wall of China, the temples of Maya by using rudimental tools.
• Scheduling theory was emerged as an active research area
in the early 1950s.
•
In the 1980s, different directions were pursued in academy
and industry. Since then, the field has attracted a lot of
researcher’s attention and has become an important branch
of operations research.
• Project Scheduling and resource management
solutions are in demand throughout the world as a
fundamental tools for the survival and success of the
compagnies.
This is what can happen without effective resources management
2. Areas of Application
•
•
•
•
•
•
•
•
Production scheduling
Large volume surveillance problem
Robotic cell scheduling
Computer processor scheduling
Timetabling
Crew scheduling
Railway scheduling
Air traffic control
3. Problem Description
• The large volume surveillance problem is a complex
decision problem characterized by the employment of
mobile and fixed assets to a large geographic area in
order to accomplish the maximum number of
surveillance tasks.
• Example of surveillance problem:
- fishing boat in distress
- search of illegal immigrants
- piracy situations
3.1. Research Problematic
A set of heterogeneous and distributed resources
+
A set of surveillance tasks
Problem
What is the ‘best’ and feasible resources assignment and task
scheduling to achieve mission goals?
System constraints
3.2. Motivations
There are few works
related
model
the
resource management for
large volume surveillance
as Multi-Objective and
Multi-Mode Assignment
and Scheduling problem.
Distributed resources
Surveillance Tasks
4. Literature Review
Multi-mode
Multi-Objectif
Single mode
Assignment and
Scheduling
problem
Without
preemption
Mono-Objectif
With
preemption
Renewable
resources
Nonrenewable
resources
• Multi-Mode
• Single Mode
• Each task can be
Each task has only
accomplished
by
one
execution
one out of a set of
mode, this means
different modes.
that the duration and
the requirements for
• executing time, cost
resources
are
and
amount
of
constant.
resources depend
on
the
adopted
mode.
• Multi-Objective
We consider more
than one objective to
optimize.
we search not only the
best optimal solution
but the pareto optimal
solutions.
obj2
x
x
x
x
x x
x
x
x
x
x
x
x
x
obj 1
• Single Objective
We consider only one objective to optimize.
The main and the most used objective in
literature is the minimization of the makespan
which represents the total duration of the
project.
min
obj
• Renewable resources •
A known amount of
resources available with
its full capacity during
the planning horizon.
Example:
machines,
equipments, manpower.
Nonrenewable resources
They are limited in amount
and are not recoverable.
Example: financial budget
• Without Preemption
• With Preemption
A Task cannot be
A Task can be
interrupted once it has
interrupted
after
been started.
each integer unit of
its processing time.
Example of resolution approaches
Resolution
approaches
Heuristics
Exact
Branch & Bound
e.g.:Sprecher et al. (1997)
Heilmann (2003)
Zhu et al. (2006)
Dynamic
programming
e.g.: Li et al. (2008)
Genetic
Algorithm
Ant
Colony
Tabou
search
…
Simulated
Annealing
e.g.: Mendes et al. (2009)
e.g.: Belfares et al. (2007)
Lova et al. (2009)
e.g.: Loukil et al.(
e.g.: Lee et Lee (2003)
Ben Abdelaziz et al. (2007)
Lo et al. (2008)
5. Proposed Model
Multi-Objectif
Multi-mode
Resource Assignment
and Scheduling
problem
Renewable
resources
without
Preemption
Mode 2
Mode 1
 Mathematical Formulation
Objectives functions
Min makespan
Z 1  max i 1,...,N
N T max M i
Min Cost
 T max M i R

t
  (t  d im k )x ijm k 
 t 1 k 1 j 1

R
t
Z 2   c j x ijm
k
i 1 t 1 k 1 j 1
1
Z

Max probability of sucess 3
N
 T max M i R
t
P
x


 ij ijm k
i 1  t 1 k 1 j 1
N
Mi
R
 q
k 1 j 1
ijm k



System constraints
Mi
N
t
t
x
q

R
 ijmk ijmk j , j  1,..., R , t  1,...,T max
i 1 k 1
T max
 tx
t 1


t
ijm k
Mi
k 1
T max
t 1
t
 T max t
Mp
R
T max x pjm k
 Max   t 1 tx pjm k   k 1  j 1  t 1
d pm k
p i 
mk

1
mk

 , i  1,..., N

t
x
 j 1 ijmk  1, i  1,..., N
R
t
x ijm
 1, i  1,..., N , j  1,..., R , k  1,...,T max
k
t
x ijm
 0,1 , i  1,..., N , j  1,..., R , k  1,..., M i , t  1,...,T max
k
The Multi-objective and Multi-mode Assignment and Scheduling
Problem
NP-Hard
• Genetic Algorithms have been implemented for
providing high-quality solutions to a wide variety of
challenging scheduling problems.
• In this work, we investigate the ability of a genetic
algorithm to effectively solve the Assignment and
Scheduling Problem
6. A Multi-criteria Genetic Approach
Chromosome representation
Each solution chromosome is made of 3n genes ( n: number of tasks)


chromosome   gene1 ,..., gene N , gene N 1 ,..., gene 2 N , gene 2 N 1 ,..., gene 3N 


period
priority
mod e


Genetic operators
Selection: elitism method
Crossover: random key
Mutation
Selection Operator
• Consists of retaining the best individuals from the
current population into the next generation based on
their fitness value. This selection method is called
elitist or elitism.
• It forms a succesful selection strategy used to ensure
that the best solutions are preserved in the next
generation and allows to converge towards the
pareto frontier.
Crossover Operator
• Two
individuals
are
randomly
selected from the current population
to act as parents.
• For each gene a random number
between [0,1] is generated. If the
generated number is smaller than a
threshold value, the gene of the first
parent is copied into the offstring
chromosome. Otherwise, the gene of
the second parent is used.
• The threshold value is an input data
and is called Crossover Probability.
Mutation Operator
• Randomly applied to explore other areas in the
solution space and avoid the convergence caused by
selection and crossover operators.
• The probability of the mutation Mr is inversely
propotional to the population size.
• After the crossover has occurred, an individual can
be selected from the current population for mutation.
It consists to switch the mode associated to the
selected task i based on its neighborhood set Hi of
the resources’ combination.
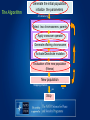
The Algorithm
Generate the initial population
initialize the parameters
At iteration g
Select two chromosomes parents
Apply crossover operator
Generate offstring chromosome
Activate/Deactivate mutation
Evaluation of the new population
(fitness)
New population
Stopping criterion
yes
Stop
no
The experimental results
• Cardinality of the approximation set
Ns
• Diversity of the approximation set
1
Ds 
N
 nik 
nik
1
Mi
i 1 H i , avec H i   log(M ) k 1 pop log  pop 
i
size
size 

N
• Diversity of the pareto approximation front
Cov Z i 
max x , y Pknown Z i (x )  Z i ( y )
Z  Z i*
*
i
100, i  {1, 2,3}
Wilcoxon signed –rank test
 level : 0.05
At confidence level : 95.5%
• As we address simultaneously assignment and scheduling problem
• While the proposed approach is effective for medium assignment and
scheduling problem,
• The proposed model becomes computationally intractable for large
sized problem when adding some realistic assumptions.
• Hence, we propose a rigorous bi-level decomposition model that
reduces the computational effort of the problem
• We decompose the original problem into an upper and a lower level.
7. The bi-level ASP
Upper level: Scheduling
Objectif
 Minimize the makespan
Constraints
 Task
 precedence constraints
 time window
 priority
 localization
Lower level: Assignment Problem
Objectif
 Minimize the total cost
Constraints
 Resources
 Availability
 fuel constraints/autonomy
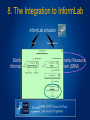
8. The Integration to InformLab
InformLab simulator
Goals
SituationEvidence
Distributed Dynamic
Distributed Dynamic Resource
Information Fusion (DIF)
Management (DRM)
Decision
•
Cooperative Search need to be detected:•
‘fish boat in distress’
Non-Cooperative Search attemps to avoid detection:
‘illegal immigrants’
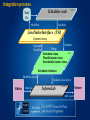
Integration process
Scheduler code
Data
File
C/C++
Schedules
ModePlan
JavaNativeInterface (JNI)
Dynamic library
Input data
ModePlan
Schedules
Proxy
Java
Scheduler class
PlansExtractor class
ScheduleConverter class
Scheduler Interface
ModePlan objects
Editor
XML files
Schedules (Java object)
InformLab
Testbed
Viewer
XML vignette
9. Conclusion
• we proposed a new formulation for the resource allocation and
tasks scheduling for large volume surveillance problem.
• A Multi-criteria GA it was developed to solve the problem
formulation
• The approach was tested using InformLab Multi-agent simulator
• We will propose an alternative model based on the bi-level
formulation