Download Towards efficient breeding

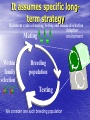
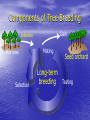
Breeding cycler:
Efficient long-term
cycling strategy
Darius Danusevičius and Dag
Lindgren
How carry breeding ?
More
gain
How to select?
phenotype?
clones?
progeny?
More
diversit
y
Faster
But the
budget is
so low...
1
$
Contents of 40 min.
General Breeidng cycler (10 min.)
Example of what cycler can do?
Testing strategy: optimization and timing (50 min):
Single-stage strategies compared,
Two-stage strategies compared,
Amplified case: Progeny testing versus Pheno/Progeny.
Main finding separately for pine and spruce (5
min.)
New Cycler and other deterministic worksheets
(Seed orchard optimizer)
Answer is
Breeding cycler
Deterministic optimizer of one (of many
identical) breeding cycles made in Excel
Transparent
Interactive
Basic feature
Complete comparison, as it simultaneously
considers:
Cost
Gain per
time
Diversity
Other things,
e.g. to well
see the road
It assumes specific longterm strategy
Recurrent cycles of mating, testing and balanced selection
Adaptive
Mating
environment
Within
family
selection
Breeding
population
Testing
We consider one such breeding population
Key-problem: How to deal with relatedness
and gene diversity
Solution: Group coancestry (equivalent
Status number, Dag Lindgren et al.)
Let's put all homologous genes in a pool
Take 2 (at random with replacement).
The probability for IBD is group coancestry.
f
Gene diversity and coancestry
GD 1  
GD = 1 - group coancestry = the probability that
the genes are non-identical, thus diverse.
Group coancestry is a measure of gene
diversity lost!
Components of Tree Breeding
Gain
Initiation
Plus trees
Selection
Mating
Long-term
breeding
Seed orchard
Testing
Long term breeding goes on for
many repeated cycles
Mating
Long-term
breeding
Selection
Testing
Breeding cycler studies what
happens in one complete cycle
Mating
Selection
Long-term
breeding
Testing
What happens in one complete cycle?
The breeding value increases
The gene diversity
decreases
Long-term
breeding
How to assign a single value to the
increase in BV and the decrease in GD?
Answer is : Group merit
weighted average of
Breeding Value and Gene
Diversity
Weighting factor = “Penalty coefficient”;
(coancestry of 1 means drop in BV dawn to 0)
if coancestry of 1= 100% drop in BV, then
coancestry of 0.005= 0.5 % drop in BV
Lindgren and Mullin 1997
During one complete cycle
The cycle takes a number of years, depending on the
duration of testing, mating and different waiting
times
Mating
Selection
Long-term
breeding
Testing
How to consider the cycle time?
Answer is: express Group Merit per
year to consider 3 key factors:
• Genetic gain;
• Gene diversity;
• Time.
Wei and Lindgren 2001
How to consider the cost?
Cost of a cycle is depending on number of test plants,
mating techniques, testing strategy etc.
Mating
Selection
Long-term
breeding
Testing
Annual Group Merit progress at a given
annual cost considers four key factors:
• Genetic gain;
• Gene diversity;
• Time;
• Cost.
Danusevicius and Lindgren 2002
Examples of what Breeding
Cycler can do
•Which is the best testing strategy
•What is optimum breeding population size?
•What is the influence of the parameters?
•When to select and what numbers to test ?
•Where to allocate resources to strengthen your
breeding plan?
•How to optimize balance among BP members?
How the Cycler works (in principle)
Size of breeding
population?
1. Input
•Genetic parameters
Mating
•Time components
•Cost component
2. Find resource
allocation that
maximises
GM/year?
Selection
age ?
Test method
Clone?
Progeny?
Long-term
breeding
Testing
size ?
Breeding cycler is based on within
family selection
Acknowledgement: Large thanks to Swedish
breeding for giving us the justification to
construct a reasonable simple breeding cycler,
that is balanced and where each breeding pop
member get exactly one offspring in next
generation breeding population. Loss of gene
diversity is only a function of Breeding
Population Size. It would have been much
harder without this simplification!
DaDa
How the Cycler works (detail)
Insert red values. The worksheet will calculate the blue values with the
consequences of your choices.
Find optimum testing size and testing time to fit into the budget and
annual maximize group merit.
Or let “SOLVER” find the values which maximise progress in group
merit
How the Cycler works
Results
You do almost nothing – input the parameters and look for
result
Variables - Genetic parameters
Additive variance in test
Dominance variance in test
Environmental variance in test
Coefficient of variance for additive “value for
forestry” at mature age
Breeding population size
Time and cost components
Cycle cost
Under budget
constraint
•Recombination (cost can be either per BP member
or in total)
•Cost per tested genotype (it costs to do a clone or a
progeny)
•Test plant can be economical unit
Cycle time
•Recombination
•Time for e.g. cloning or creation of progeny
•Production of test plants
•Testing time
Variables - Others
Rotation time (for J*M considerations)
Annual budget
Test method (clonal, progeny or phenotype)
J*M development curve
Weighting factor for diversity versus gain
J-M correlation is important
Lambeth and
Dill 2001
(genetic) is our
favourite.
0.8
J-M correlation
Choice can be
made of J-M
function
including
custom,
1.0
0.6
0.4
0.2
Lambeth (1980)
Lambeth (2001)
Gwaze (2000)
Custom
0.0
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Ratio selection/rotation age (Q)
Constraints and limitations
of breeding cycler
Sh…. in – sh… out, thus the input values must be
chosen with care
The input values may need an adjustment from the
most evident for considering factors not considered
in the math
Breeding heads for an area and get information from
a number of sites, this is considered by
modification to the variance components
Breeding heads for improvement in many characters,
we the goal as one character “value for forestry”.
The “observation” is an index of observations, and
J*M has to be adjusted.
Constraints and limitations of
breeding cycler - continued
Plant cost is seen as independent of age of
evaluation. This can cause problems for
some type of comparisons.
It is rather easy to add many type of
considerations to the EXCEL sheet, the
problem is that it makes it too complex for
the user journal papers.
Cycling will accumulate gain.
Where is the limit?
Example of what
Breeding cycler can do
studies by Dag and
Darius
Contents
Optimizing the
balance
Seminar 2009
3: Ph/Prog amplified
(pine), effect of J-M.
shark
Best testing
strategy
Breeding
cycler
Main findings
•Clonal test is superior (use for spruce)
•Progeny testing not efficient
•For Pine, use 2 stage Pheno/Progeny
•If 2stage is used, pine flowers not needed
before age ~ 10-15
•Optimizing the balance may give 50%
more gain
General M&M
Main inputs and scenarios
Low
Main
High
Genetic parameters
lower typical for higher
Time components reasonable Pine or reasonable
bound
spruce
bound
Cost components
While testing an alternative parameter value,
the other parameters were at main scenario
values
Time compnents
Time components of complete breeding cycle
Stage 2. Time after: from selection
of new individuals to start of their
flowering (crosses for the next cycle
can be made). If the selected
individuals flower, Time after = 0.
Recombination time:
pollen collection, crossing, seed
maturation…
TAfter
TRecomb
TBefore
Stage 2. Testing:
from establishment to
selection
Ttest
Stage 2. Time before:
test plant production
Breeding
cycle
TBefore
TAfter
Ttest
Stage 1. Time before:
test plant production
Stage 1. Testing:
from establishment to
selection
Stage 1. Time after: from selection
of candidates to their reproductive
maturity. If the candidates are
reproductively mature, Time after = 0.
The time and cost explained
•Cost per test plant = 1 ’cost unit’, all the other costs
expressed as ratio of this 1.
•Such expression also helped to set the budget
constraint corresponding to the present-day budget
Production of Cutting of
sibs (4 years) ramets
Crossing
Genotype
Recombination
depend. cost=2
cost=20,
(per ortet)
Time=4
Mating time
Established in
5 years after
seed harvest
Rooting of
ramets (1 year)
Transportation
Nursery
Establishment,
maintenance and
assessments
Field trial
Plant dependent cost=1 (per ramet)
Time before
Testing time Lag
All these costs should fit to a
present-day budget
Budget estimate is taken from pine and spruce
breeding plan ~ test size expressed per year and BP
member.
~ 10 ’cost units’ for pine, 20- for spruce.
ng of
Rooti year)
s (1
ramet
of
tting
f Cu mets
o
n
o
i
ra
d u ct
Pro
rs)
4 yea
sibs (
type
sing
Geno st=0.1
Cros
ation epend. co t)
mbin
d
o rt e
Reco 20-50,
(per
cost= =3
Time
time
g
n
i
t
Ma
Field
p or
Trans
ery
Nurs
ent,
lishm
Estab ance and
en
maint sments
asses
in
lished
Estab s after
r
5 yea rvest
ha
d
e
e
s
d
Plant
e
befor
e
m
i
T
tation
epen
e r ra
t=1 (p
s
o
c
t
den
trial
met)
e Lag
m
i
t
ng
Testi
How optimization works under
specific scenario?
• Optimization= optimum
combination of testing time and
testing size to obtain max
GM/Year and to satisfy the budget
constraint (use Solver)
Single-stage
testing
strategies
Objective: compare strategies based on
phenotype, clone or progeny testing
Clone or progeny testing
Phenotype testing
N=50
N=50
(…n)
(…n)
(…n)
OBS: Further result on
numbers and costs- for one of
these families
(…n)
(…m)(…m)(…m) (…m)(…m)(…m)
(…n), (…m) and selection age were optimized
Parameters- for reference
Parameters
Main scenario
Alternative scenarios
Additive variance (sA2 )
1
Dominance variance, % of the additive variance in BP (sD2)
25
0; 100
Narrow-sense heritability (h2) (obtained by changing sE2)
0.1
0.05; 0.5
Additive standard deviation at mature age (sAm), %
10
5; 20
Diversity loss per cycle, %
0.5
0.25;1
Rotation age, years
60
10; 120
1 (phenotype)
3; 5 (phenotype)
5 (clone)
3; 7 (clone)
17 (progeny)
5; 7 (progeny)
30
15; 50
0.1 (clone),
1; 5 (clone),
1 (progeny)
0.1; 5 (progeny)
Cost per plant (Cp), $
1
0.5; 3
Cost per year and parent (constraint)
10
5; 20
Time before establishment of the selection test (TBEFORE), years
Recombination cost (CRECOMB), $
Cost per genotype (Cg), $
Group Merit Gain per year (GMG/Y)
To be maximized
CVa at mature age
• CVa=14 % is based on pine tests in south
Sweden Jansson et al (1998),
• 1/2 of additive var in pop is within full sib
families,
• Our program is balanced= gain only from
within full-sib selection,
• Thus, CVa within fam= CVa in pop divided
by the square root of 2, thus a CV = 10%.
CVa within = sqrt(s2/2)= sqrt(s2)/sqrt(2)= s2/sqrt(2)
Test 26 clones with 21 ramet
(18/15  budget), select at age 20
Test 182 phenotypes; select at
age 15, ( budget: 86, for 17
years) (second best)
Test 11 female parents with 47
progeny each; select at age 34 (
budget: 8/34, 40 years)
Annual Group Merit, %
Results-clonal best, progeny worst
0.6
0.5
0.4
0.3
0.2
0.1
0.0
Clone
Phenotype
Progeny
0 0.1 0.2 0.3 0.4 0.5 0.6
Narrow-sense heritability
At all the scenarios, Clonal was
superior, except high h2.
GM/Y digits after comma are important
• If for Clone GM/Y=0.25%; cycle= 30
years then
• Cycle GM=8 % (gain 8.5 - 0.5 div loss)
• Thus GM/Y reduction by 0.03 (10%) =
Cycle gain reduction by 1%
• Loss of Cycle gain by 1% = important
loss
How flat are the optima (clone)?
h2=0.1, lower budget, at optimum testing time
This means: If problems
with cloning, better->
clones with < ramets
0.30
Optimum 18(15)
Annual Group Merit , %
No marked effect: 12
clones with 22 ramets or
30 clones with 10 ramets.
0.25
0.20
GM/Y by Pheno
0.15
0.10
4(59) 10(25) 15(18) 20(14) 30(10) 40(8)
Clone no (ramets per clone)
Test time 17
18
20
22
23
25
If not enough cuttings, better more clones with less ramets,
rather than to reduce ramet number at optimum clone number
testing
time
70(5)
57(6)
50(7)
45(8)
39(9)
32(11)
30(12)
28(13)
26(14)
24(15)
22(16)
21(18)
20(18)
19(19)
0.450
0.440 0.436
0.430
0.420
0.410
This line marks loss of GM/Y > 0,03
0.400
0.390
0.380
GM/Y by Phenotype=0,275
0.370
0.360
0.350 Variation in these outlined numbers will
0.340 not cause marked loss of benefit
0.330
36(10)
Budget=20, h2=0.1, Cycling cost=20, time 4, Tbefore=5, Cg=2, J-M corr by L(2001), c=100
Optimum for clone number (ramet no per clone)
12 12 12 12 12 13 13 13
14 14 15 15 15 15 17
Higher
2
h
= more clones and
less ramets
Clone no/ramet no
0.50
0.40
GM/Y, %
Optimum then is
between 18/15 and
30/10
46/5
18/15
0.30
0.20
Spruce plan 40/15
0.10
Ola’s thesis, paper I, Fig.
9= 40 cl with 7 ram at test
size 280
0.00
28/9
13/23
0
0.1
0.2
0.3
0.4
0.5
Narrow-sense heritability
Budget= 10
The optimal testing time
•These 18-20 years
with conservative
J-M function
(Lambeth 1980)
•With Lambeth
2001, about 15-17
years
0.30
Annual Group Merit, %
•No effect to test
longer than 18-20
years
Clone strategy
0.25
0.20
0.15
0.10
0.05
0.00
15 16 17 18 19 20 21 22 23 24 25
Testing time, years
Figure with optimum at main scenario parameters (budget=10) clones/ramets 18/15
How realistic are the optima?
• Optima depends on budget, h2, J-M
correlation- how realistic are they?
1. Budget is the present-day allocation.
Increase will result in more gain. But we test
how to optimise the resources we have.
2. h2 =0,1 seems to be reasonable
3. J-M functions taken from southerly pines, it
affects the timing with stand. error of 2
years (7-10-12).
Why Phenotype ≥Progeny ?
• Drawbacks of Progeny: long time and high
cost (important to consider for improvement)
• Phenotype generates less gain but this is
compensated by cheaper and faster cycles.
Dominance would
not markedly affect
superior
performance of
clonal testing
Annual Group Merit, %
Dominance seems to matter little
0.6
0.5
0.4
0.3
0.2
0.1
0.0
Clone
Phenotype
Progeny
0
25 50 75 100 125
Dominance variance (% of
additive)
Expensive genotypes are of interest only if it would
markedly shorten T before for Progeny or improve cloning
So it pays off to make expensive cloning
0.30
0.25
0.30
0.25 Tbefore
On Genotype cost
Clone
0.20
0.20
0.15
Clone
Progeny
0.15
Progeny
0.10
0.10
Phenotype
0.05
0.05
0 1 2 3 4 5
Cost per genotype
6
0 3 6 9 12 15 18
Delay before establishment of
selection test (years)
Mating cost and total budget
Annual Group Merit , %
0.3
0.30
Clone
Clone
0.25
Phenotype
0.2
0.20
Phenotype
0.15
0.1
Progeny
Progeny
0.10
0.0
0.05
0
5
10
15
20
Budget per year and parent
25
10
20
30
40
50
60
Recombination cost
Important factor, we used If there is need, mating
present-day figures; what can be expensive
happens if it fluctuates
Conclusions
• Clonal testing is the best breeding strategy
• Phenotype 2nd best, except very low h2
• Superiority of the Phenotype over Progeny is
minor = additional considerations may be
important (idea of a two-stage strategy).
Let’s do it in 2
stages?
Phenotype/Progeny strategy
(70)
(70)
(30) (30)(30)(30)(30) (30) (30)(30)(30)(30)
Stage 1 Phenotype
select at age 10 (15
only 3% GM lost)
Stage 2 Progeny
test select at ca 10
Values- study 2
Parameters
Main scenario
Additive variance (sA2 )
Dominance variance, % of the additive variance in
2
BP (sD )
Environmental variance, % of total variance s
( E2 )
Additive standard deviation at mature age(sAm), %
Diversity loss per cycle, %
Rotation age, years
1
Alternative
scenarios
-
25
0; 100
Time before establishment of the selection test
(TBEFORE), years
Recombination cost (CRECOMB ), $
Cost per genotype (Cg), $
Cost per plant (Cp), $
Budget per year and parent (the constraint)
Group Merit Gain per year (GMG/Y)
88
0; 38; 94
10
5; 20
0.5
0.25;1; 5
60
10; 20; 120
1 (phenotype)
3; 5 (phenotype)
5 (clone;
3; 7 (clone;
phenotype/clone) phenotype/clone)
17 (progeny;
5; 7 (progeny;
phenotype/progeny) phenotype/progeny)
30
0.1 (clone),
1; 5 (clone),
1 (progeny)
0.1; 5 (progeny)
1
0.5; 3
10
5; 20; 50
To be maximized
Results: two-stage 2nd best
•Clone = Phenotype/Clone
= no need for 2 stages.
0.30
Clone
0.25
•Phenotype/Progeny is 2nd 0.20
best = best for Pine
•If Progeny initiated early,
may~ Phenotype/Progeny
= need for a amplification
•Phenotype/Progeny is shown with
a restriction for Phenotype
selection age > 15
Pheno/Progeny
0.15
Phenotype
Progeny
0.10
1
3 5
7
9 11 13 15 17
Delay before establishment of
selection test (years)
arrows show main scenario
If budget is cut
by half = simple
Phenotype test
Annual Group Merit, %
Budget cuts = switching to
Phenotype tests in Pine
0.3
Clone
Pheno/Progeny
0.2
Phenotype
Progeny
0.1
0
5
10
15
20
Budget per year and parent (%)
Budget cuts for Pheno/Progeny
Genetic gain, %
Budget =
resources
reallocated on
cheaper
Phenotype test
5
32
Stage 2 Progeny
4
17
3
5(44)
Stage 1
5(72)
Phenotype
2
Budget=10
Budget=5
Testing time 10 (stage 1) and 14 (stage 2) little affected by
the budget
Why Pheno/Progeny was so good?
• It generated extra gain by taking advantage
of the time before the candidates reach
their sexual maturity
• This was more beneficial than single-stage
Progeny test at a very early age
• Question for the next study: is there any
feasible case where Progeny can be
better?
Progeny test with and without
phenotypic pre-selection
• Is there any realistic situation where
Progeny testing is superior over
Pheno/Progeny (reasonable interactions and
scenarios)
• What and how flat is the optimum age of
pre-selection for Pheno/Progeny? (when do
we will need flowers?)
Phenotype test
Pre-selection
age?
Progeny test
Time and cost components
CPer CYCLE = Crecomb + n (CG + m CP),
Tcycle = Trecomb + TMATING + TLAG + Tprogtest
TMATING age of sufficient flowering capacity to initiate
progeny test (for 2-stage strategy it corresponds to the age
of phenotypic pre-selection
TLAG is crossing lag for progeny test (polycross, seed maturation,
seedling production)
Parameters study 3
Main scenario
values
Alternative
scenario values*
Interactive
scenario values
Additive variance (sA2 )
1
-
-
Dominance variance, % of the additive variance
(sD2)
25
0; 100
-
Narrow-sense heritability (h2) (obtained by
changing sE2)
0.1
0.01; 0.5
0.01
Additive standard deviation at mature age %
10
-
-
Diversity loss per cycle, %
0.5
-
-
L (2001)
L(1980); G(2000)
L(1980)
3 to 25 by 1
-
-
Crossing lag for progeny test (crossing; seed
maturation, seedling production),years
3
5; 8
-
Rotation age (RA), years
50
20; 30; 80
80
Recombination cost (CRECOMB), $
30
0; 100
-
Cost per genotype (Cg), $
1
0.1; 10
-
Cost per plant (Cp), $
1
0.1; 2
-
Budget per year and parent, $ (the constraint)
10
5; 20
-
Parameters
J-M genetic correlation function
Age of mating for progeny test (age of sufficient
flowering capacity for progeny testing), years
Annual progress in Group Merit (GM/Y)
1
To be maximized
J-M correlation functions
•
•Gwaze et al. (2000)=
genetic correlations from 19
trials with 190 fams of P
taeda western USA.
•Lambeth (1980)= phenotypic
fam mean corrs from many
trials of 3 temperate conifers
J-M genetic correlation coefficient
•Lambeth (2001) Main =
genetic corrs in 4 series (15
trials) P taeda (296 fams)
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
Lambeth (1980)
Lambeth & Dill (2001)
Gwaze et al. (2000)
0.0
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Ratio selection/rotation age (Q)
• 2 stage strategy
was better under
most reasonable
values
•No marked loss
would occur if
mating is postponed
to age 15
Annual Group Merit (%)
Results: 2 stage is better
Main scenario
0.6
Pheno/Progeny
0.3
Progeny
0.0
0
5 10 15 20 25
Age of mating for progeny
test (years)
J-M correlation affects pre-selection age
•The gain generating
efficiency mainly depends
on slope of J-M correlation
function.
•
1.0
J-M genetic correlation coefficient
•Optimum selection age
depends on efficiency of
Phenotype to generate
enough gain to motivate
prolongation of testing for
an unit of time.
0.9
0.8
10
0.7
0.6
0.5
0.4
0.3
0.2
0.1
7
Gain would increase
faster if switching to
12 progeny test
Gain increases
fast by time
Lambeth (1980)
Lambeth & Dill (2001)
Gwaze et al. (2000)
0.0
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Ratio selection/rotation age (Q)
Do we have J-M estimates for spruce and pine?
When the loss from optimum is
important?
Annual Group Merit (%)
When early testing is advantageous
Rotation age = 20
0.6
2
0.8
h = 0.5
Plant cost= 0.1
0.6
Pheno/Progeny
0.6
0.4
0.3
0.3
0.0
0.0
Progeny
0.2
0.0
0
5 10 15 20 25
0
5 10 15 20 25
0
5 10 15 20 25
Age of mating for progeny test (years)
h2 is high but then
Phenotype alone is
better
Rotation is short
Plants are cheap
Annual Group Merit (%)
Better crossings are motivated
Crossing lag= 5
0.5
0.4
0.4
Pheno/Progeny
10; 0.26
0.3
0.2
0.23
Progeny
0.3
0.1
0.0
0.0
5 10 15 20 25
10; 0.25
0.22
0.2
0.1
0
Crossing lag= 8
0.5
0
5 10 15 20 25
Age of mating for progeny test (years)
Crossing lag and genotype costs had no marked effect
= the crosses can be made over a longer time to
simultaneously test all pre-selected individuals and
their flowering may be induced at a higher cost.
These are as for our
interactive scenario:
•low heritability (0,01),
•long rotation (80 y)=
less J-M at pre-selection,
•weak J-M correlation
(L1980)
Annual Group Merit (%)
Progeny is motivated when
conditions disfavour Phenotype
Interactive scenario
0.06
Pheno/Progeny
Progeny
0.03
0.00
0
5 10 15 20 25
Age of mating for progeny test
(years)
But the optima flat and scenario unrealistic
Optimum test time and size for pine
(for one of the 50 full sib fams)
Cycle time~ 27
Gain=8 %
GM/Y= 0,27%
Select back the
best of 5 when
progeny- test
age is 10
Stage 2. Progenytest each of those 5
with 30 offspring
2-4 years, at a high
cost if feasible
Mating
Long-term
breeding
Lag- 3-4
years
Stage 1: Test
70 full-sibs
Select 5 at age 10
What if no pine flowers until age 25?
•Progeny is the last
•Budget cuts, high h2 will
favour Phenotype
0.15
0.179
0.135
0.140
Phenotype
•Phenotype with selection age
of 25 is better
0.20
Progeny
•Pheno/Progeny is still leading
Annual Group Merit, %
This means, singe stage Phenotype cycle time > 25
years and For the two-stage, pre-selection not at its
Main (h=0.1, budget=10), Flowers at age 25
optimum age (10 years)
0.10
0.05
0.00
Pheno/
Progeny
May be 2 cycles of Phenotype
instead of Pheno/Progeny?
Phenotype
Cycle, GM/year, GM/cycle 2 cycle s
years %
of Pheno
20
0,152
3,04
6,08
Pheno/Prog 40
0,181
Answer is No: 7,26 is > 6,08
7,26
Conclusions
•Under all realistic values, Pheno/Progeny
better than Progeny
•Sufficient flowering of pine at age 10 is
desirable, but the disadvantage to wait until
the age of 15 years was minor,
•If rotation short, h2 high, testing cheap,
delays from optimum age could be
important
Main findings: cloning is the best strategy
Our main findings
Main findings- spruce
Clonal test by far the best
If higher h2
more clones
less ramets
Present plans:
size 40/15,
selection age:
10 years
(18)
(18)
Select at age 15
(20) depending on
J-M correlation
(15) (15) (15) (15) (15) (15)
With L(2001), Cycle time~ 21 Gain=8.2 % GM/Y=
0,34%
Main findings- Pine
Use 2 stage Pheno/Progeny strategy
(70)
(70)
(30) (30)(30)(30)(30) (30) (30)(30)(30)(30)
Stage 1 Phenotype
select at age 10 (15
only 3% GM lost)
Stage 2 Progeny
test select at ca 10
With L(2001), Cycle time~ 27 Gain=8 % GM/Y=
0,27%
Research needs- Faster cloning
Research needs (a PhD thesis)
•Faster, better cloning: embryogenesis, rooting,
C-effects (especially for pine)
•Sufficient flowering at age 10 (15) for pine
•Documentation of flowering in breeding stock
•How sexual maturation, flowering abundance
are related to breeding value?
Optimizing the
Balance: restrict
grandparental but
relax parental
contributions
Balanced long-term breeding
Some unbalance has advantages in long
term breeding
The inoptimality loss seem to be small; it is
tricky to utilize inbalance, and the balance
is unlikely to affect most of the
recommendations much.
Unbalance at initiation of breeding
At initiation of breeding there is no
“balance”. Truncating tested plus trees to
long term breeding has sometimes been
done with inoptimal unbalance in the
Swedish breeding program. I believe it is
more optimal to sacrify the gene diversity in
the initial selection a bit slower. This has
been discussed i förädlingsrådet 1999, and
one argument is in Routsalainen’s thesis
(2002), so I will not discuss this more here.
SPM parental balance
(almost current Swedish pine
program)
Founder selection
Mating of founders
Select and mate 2 best sibs to
create 2 families
Cycle 1
(…)
(…)
Select and mate 2 best sibs to
create 2 families
Cycle 2
(…)
(…)
Select and mate 2 best sibs to
create 2 families
Cycle 3
(…)
(…)
Green trees
show pedigree
Multiple SPMs
Founders
(…)
Cross e.g. 4 best sibs in the 2 best
families
(…)
1st rank family
(…)
1st
rank family
(…)
(…)
nth rank family
3rd rank family
(…)
2nd rank family
(…)
(…)
3rd rank family
(…)
nth rank family
(…)
2nd rank family
Multiple SPMs
Pedigrees BP third generation
Founders
(…)
(…)
(…)
Pedigree to later breeding
population
Trees selected for crossing
in the 3rd generation
1st
rank family
(…)
2nd rank family
Note that retrospectively SPM and multiple
SPM give identical pedigrees, thus
identical increase of coancestry.
.
Families & parents cost nothing
0.6
14
Annual progress (%)
0.5
10
High budget
0.4
5
0.3
0.2
Medium budget
Low budget
0.1
0.0
0
2
2=phenotypic
5
10
15
20
Number of parents per selected family
25
Families & parents are expensive
Annual progress (%)
0.6
0.5
High budget
7
0.4
4
0.3
Medium budget
0.2
Low budget
(impossible)
0.1
0.0
0
2
5
10
15
20
Number of parents per selected family
Conclusions
• Multiple SPM strategy is VERY promising and
can beat conventional single SPM strategy
with 20-70 % gain. Variants of strategy 5
which are still more efficient can be
constructed.
The end