* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Towards efficient breeding
Survey
Document related concepts
Transcript
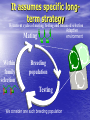
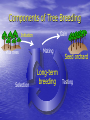
Breeding cycler: Efficient long-term cycling strategy Darius Danusevičius and Dag Lindgren How carry breeding ? More gain How to select? phenotype? clones? progeny? More diversit y Faster But the budget is so low... 1 $ Contents of 40 min. General Breeidng cycler (10 min.) Example of what cycler can do? Testing strategy: optimization and timing (50 min): Single-stage strategies compared, Two-stage strategies compared, Amplified case: Progeny testing versus Pheno/Progeny. Main finding separately for pine and spruce (5 min.) New Cycler and other deterministic worksheets (Seed orchard optimizer) Answer is Breeding cycler Deterministic optimizer of one (of many identical) breeding cycles made in Excel Transparent Interactive Basic feature Complete comparison, as it simultaneously considers: Cost Gain per time Diversity Other things, e.g. to well see the road It assumes specific longterm strategy Recurrent cycles of mating, testing and balanced selection Adaptive Mating environment Within family selection Breeding population Testing We consider one such breeding population Key-problem: How to deal with relatedness and gene diversity Solution: Group coancestry (equivalent Status number, Dag Lindgren et al.) Let's put all homologous genes in a pool Take 2 (at random with replacement). The probability for IBD is group coancestry. f Gene diversity and coancestry GD 1 GD = 1 - group coancestry = the probability that the genes are non-identical, thus diverse. Group coancestry is a measure of gene diversity lost! Components of Tree Breeding Gain Initiation Plus trees Selection Mating Long-term breeding Seed orchard Testing Long term breeding goes on for many repeated cycles Mating Long-term breeding Selection Testing Breeding cycler studies what happens in one complete cycle Mating Selection Long-term breeding Testing What happens in one complete cycle? The breeding value increases The gene diversity decreases Long-term breeding How to assign a single value to the increase in BV and the decrease in GD? Answer is : Group merit weighted average of Breeding Value and Gene Diversity Weighting factor = “Penalty coefficient”; (coancestry of 1 means drop in BV dawn to 0) if coancestry of 1= 100% drop in BV, then coancestry of 0.005= 0.5 % drop in BV Lindgren and Mullin 1997 During one complete cycle The cycle takes a number of years, depending on the duration of testing, mating and different waiting times Mating Selection Long-term breeding Testing How to consider the cycle time? Answer is: express Group Merit per year to consider 3 key factors: • Genetic gain; • Gene diversity; • Time. Wei and Lindgren 2001 How to consider the cost? Cost of a cycle is depending on number of test plants, mating techniques, testing strategy etc. Mating Selection Long-term breeding Testing Annual Group Merit progress at a given annual cost considers four key factors: • Genetic gain; • Gene diversity; • Time; • Cost. Danusevicius and Lindgren 2002 Examples of what Breeding Cycler can do •Which is the best testing strategy •What is optimum breeding population size? •What is the influence of the parameters? •When to select and what numbers to test ? •Where to allocate resources to strengthen your breeding plan? •How to optimize balance among BP members? How the Cycler works (in principle) Size of breeding population? 1. Input •Genetic parameters Mating •Time components •Cost component 2. Find resource allocation that maximises GM/year? Selection age ? Test method Clone? Progeny? Long-term breeding Testing size ? Breeding cycler is based on within family selection Acknowledgement: Large thanks to Swedish breeding for giving us the justification to construct a reasonable simple breeding cycler, that is balanced and where each breeding pop member get exactly one offspring in next generation breeding population. Loss of gene diversity is only a function of Breeding Population Size. It would have been much harder without this simplification! DaDa How the Cycler works (detail) Insert red values. The worksheet will calculate the blue values with the consequences of your choices. Find optimum testing size and testing time to fit into the budget and annual maximize group merit. Or let “SOLVER” find the values which maximise progress in group merit How the Cycler works Results You do almost nothing – input the parameters and look for result Variables - Genetic parameters Additive variance in test Dominance variance in test Environmental variance in test Coefficient of variance for additive “value for forestry” at mature age Breeding population size Time and cost components Cycle cost Under budget constraint •Recombination (cost can be either per BP member or in total) •Cost per tested genotype (it costs to do a clone or a progeny) •Test plant can be economical unit Cycle time •Recombination •Time for e.g. cloning or creation of progeny •Production of test plants •Testing time Variables - Others Rotation time (for J*M considerations) Annual budget Test method (clonal, progeny or phenotype) J*M development curve Weighting factor for diversity versus gain J-M correlation is important Lambeth and Dill 2001 (genetic) is our favourite. 0.8 J-M correlation Choice can be made of J-M function including custom, 1.0 0.6 0.4 0.2 Lambeth (1980) Lambeth (2001) Gwaze (2000) Custom 0.0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Ratio selection/rotation age (Q) Constraints and limitations of breeding cycler Sh…. in – sh… out, thus the input values must be chosen with care The input values may need an adjustment from the most evident for considering factors not considered in the math Breeding heads for an area and get information from a number of sites, this is considered by modification to the variance components Breeding heads for improvement in many characters, we the goal as one character “value for forestry”. The “observation” is an index of observations, and J*M has to be adjusted. Constraints and limitations of breeding cycler - continued Plant cost is seen as independent of age of evaluation. This can cause problems for some type of comparisons. It is rather easy to add many type of considerations to the EXCEL sheet, the problem is that it makes it too complex for the user journal papers. Cycling will accumulate gain. Where is the limit? Example of what Breeding cycler can do studies by Dag and Darius Contents Optimizing the balance Seminar 2009 3: Ph/Prog amplified (pine), effect of J-M. shark Best testing strategy Breeding cycler Main findings •Clonal test is superior (use for spruce) •Progeny testing not efficient •For Pine, use 2 stage Pheno/Progeny •If 2stage is used, pine flowers not needed before age ~ 10-15 •Optimizing the balance may give 50% more gain General M&M Main inputs and scenarios Low Main High Genetic parameters lower typical for higher Time components reasonable Pine or reasonable bound spruce bound Cost components While testing an alternative parameter value, the other parameters were at main scenario values Time compnents Time components of complete breeding cycle Stage 2. Time after: from selection of new individuals to start of their flowering (crosses for the next cycle can be made). If the selected individuals flower, Time after = 0. Recombination time: pollen collection, crossing, seed maturation… TAfter TRecomb TBefore Stage 2. Testing: from establishment to selection Ttest Stage 2. Time before: test plant production Breeding cycle TBefore TAfter Ttest Stage 1. Time before: test plant production Stage 1. Testing: from establishment to selection Stage 1. Time after: from selection of candidates to their reproductive maturity. If the candidates are reproductively mature, Time after = 0. The time and cost explained •Cost per test plant = 1 ’cost unit’, all the other costs expressed as ratio of this 1. •Such expression also helped to set the budget constraint corresponding to the present-day budget Production of Cutting of sibs (4 years) ramets Crossing Genotype Recombination depend. cost=2 cost=20, (per ortet) Time=4 Mating time Established in 5 years after seed harvest Rooting of ramets (1 year) Transportation Nursery Establishment, maintenance and assessments Field trial Plant dependent cost=1 (per ramet) Time before Testing time Lag All these costs should fit to a present-day budget Budget estimate is taken from pine and spruce breeding plan ~ test size expressed per year and BP member. ~ 10 ’cost units’ for pine, 20- for spruce. ng of Rooti year) s (1 ramet of tting f Cu mets o n o i ra d u ct Pro rs) 4 yea sibs ( type sing Geno st=0.1 Cros ation epend. co t) mbin d o rt e Reco 20-50, (per cost= =3 Time time g n i t Ma Field p or Trans ery Nurs ent, lishm Estab ance and en maint sments asses in lished Estab s after r 5 yea rvest ha d e e s d Plant e befor e m i T tation epen e r ra t=1 (p s o c t den trial met) e Lag m i t ng Testi How optimization works under specific scenario? • Optimization= optimum combination of testing time and testing size to obtain max GM/Year and to satisfy the budget constraint (use Solver) Single-stage testing strategies Objective: compare strategies based on phenotype, clone or progeny testing Clone or progeny testing Phenotype testing N=50 N=50 (…n) (…n) (…n) OBS: Further result on numbers and costs- for one of these families (…n) (…m)(…m)(…m) (…m)(…m)(…m) (…n), (…m) and selection age were optimized Parameters- for reference Parameters Main scenario Alternative scenarios Additive variance (sA2 ) 1 Dominance variance, % of the additive variance in BP (sD2) 25 0; 100 Narrow-sense heritability (h2) (obtained by changing sE2) 0.1 0.05; 0.5 Additive standard deviation at mature age (sAm), % 10 5; 20 Diversity loss per cycle, % 0.5 0.25;1 Rotation age, years 60 10; 120 1 (phenotype) 3; 5 (phenotype) 5 (clone) 3; 7 (clone) 17 (progeny) 5; 7 (progeny) 30 15; 50 0.1 (clone), 1; 5 (clone), 1 (progeny) 0.1; 5 (progeny) Cost per plant (Cp), $ 1 0.5; 3 Cost per year and parent (constraint) 10 5; 20 Time before establishment of the selection test (TBEFORE), years Recombination cost (CRECOMB), $ Cost per genotype (Cg), $ Group Merit Gain per year (GMG/Y) To be maximized CVa at mature age • CVa=14 % is based on pine tests in south Sweden Jansson et al (1998), • 1/2 of additive var in pop is within full sib families, • Our program is balanced= gain only from within full-sib selection, • Thus, CVa within fam= CVa in pop divided by the square root of 2, thus a CV = 10%. CVa within = sqrt(s2/2)= sqrt(s2)/sqrt(2)= s2/sqrt(2) Test 26 clones with 21 ramet (18/15 budget), select at age 20 Test 182 phenotypes; select at age 15, ( budget: 86, for 17 years) (second best) Test 11 female parents with 47 progeny each; select at age 34 ( budget: 8/34, 40 years) Annual Group Merit, % Results-clonal best, progeny worst 0.6 0.5 0.4 0.3 0.2 0.1 0.0 Clone Phenotype Progeny 0 0.1 0.2 0.3 0.4 0.5 0.6 Narrow-sense heritability At all the scenarios, Clonal was superior, except high h2. GM/Y digits after comma are important • If for Clone GM/Y=0.25%; cycle= 30 years then • Cycle GM=8 % (gain 8.5 - 0.5 div loss) • Thus GM/Y reduction by 0.03 (10%) = Cycle gain reduction by 1% • Loss of Cycle gain by 1% = important loss How flat are the optima (clone)? h2=0.1, lower budget, at optimum testing time This means: If problems with cloning, better-> clones with < ramets 0.30 Optimum 18(15) Annual Group Merit , % No marked effect: 12 clones with 22 ramets or 30 clones with 10 ramets. 0.25 0.20 GM/Y by Pheno 0.15 0.10 4(59) 10(25) 15(18) 20(14) 30(10) 40(8) Clone no (ramets per clone) Test time 17 18 20 22 23 25 If not enough cuttings, better more clones with less ramets, rather than to reduce ramet number at optimum clone number testing time 70(5) 57(6) 50(7) 45(8) 39(9) 32(11) 30(12) 28(13) 26(14) 24(15) 22(16) 21(18) 20(18) 19(19) 0.450 0.440 0.436 0.430 0.420 0.410 This line marks loss of GM/Y > 0,03 0.400 0.390 0.380 GM/Y by Phenotype=0,275 0.370 0.360 0.350 Variation in these outlined numbers will 0.340 not cause marked loss of benefit 0.330 36(10) Budget=20, h2=0.1, Cycling cost=20, time 4, Tbefore=5, Cg=2, J-M corr by L(2001), c=100 Optimum for clone number (ramet no per clone) 12 12 12 12 12 13 13 13 14 14 15 15 15 15 17 Higher 2 h = more clones and less ramets Clone no/ramet no 0.50 0.40 GM/Y, % Optimum then is between 18/15 and 30/10 46/5 18/15 0.30 0.20 Spruce plan 40/15 0.10 Ola’s thesis, paper I, Fig. 9= 40 cl with 7 ram at test size 280 0.00 28/9 13/23 0 0.1 0.2 0.3 0.4 0.5 Narrow-sense heritability Budget= 10 The optimal testing time •These 18-20 years with conservative J-M function (Lambeth 1980) •With Lambeth 2001, about 15-17 years 0.30 Annual Group Merit, % •No effect to test longer than 18-20 years Clone strategy 0.25 0.20 0.15 0.10 0.05 0.00 15 16 17 18 19 20 21 22 23 24 25 Testing time, years Figure with optimum at main scenario parameters (budget=10) clones/ramets 18/15 How realistic are the optima? • Optima depends on budget, h2, J-M correlation- how realistic are they? 1. Budget is the present-day allocation. Increase will result in more gain. But we test how to optimise the resources we have. 2. h2 =0,1 seems to be reasonable 3. J-M functions taken from southerly pines, it affects the timing with stand. error of 2 years (7-10-12). Why Phenotype ≥Progeny ? • Drawbacks of Progeny: long time and high cost (important to consider for improvement) • Phenotype generates less gain but this is compensated by cheaper and faster cycles. Dominance would not markedly affect superior performance of clonal testing Annual Group Merit, % Dominance seems to matter little 0.6 0.5 0.4 0.3 0.2 0.1 0.0 Clone Phenotype Progeny 0 25 50 75 100 125 Dominance variance (% of additive) Expensive genotypes are of interest only if it would markedly shorten T before for Progeny or improve cloning So it pays off to make expensive cloning 0.30 0.25 0.30 0.25 Tbefore On Genotype cost Clone 0.20 0.20 0.15 Clone Progeny 0.15 Progeny 0.10 0.10 Phenotype 0.05 0.05 0 1 2 3 4 5 Cost per genotype 6 0 3 6 9 12 15 18 Delay before establishment of selection test (years) Mating cost and total budget Annual Group Merit , % 0.3 0.30 Clone Clone 0.25 Phenotype 0.2 0.20 Phenotype 0.15 0.1 Progeny Progeny 0.10 0.0 0.05 0 5 10 15 20 Budget per year and parent 25 10 20 30 40 50 60 Recombination cost Important factor, we used If there is need, mating present-day figures; what can be expensive happens if it fluctuates Conclusions • Clonal testing is the best breeding strategy • Phenotype 2nd best, except very low h2 • Superiority of the Phenotype over Progeny is minor = additional considerations may be important (idea of a two-stage strategy). Let’s do it in 2 stages? Phenotype/Progeny strategy (70) (70) (30) (30)(30)(30)(30) (30) (30)(30)(30)(30) Stage 1 Phenotype select at age 10 (15 only 3% GM lost) Stage 2 Progeny test select at ca 10 Values- study 2 Parameters Main scenario Additive variance (sA2 ) Dominance variance, % of the additive variance in 2 BP (sD ) Environmental variance, % of total variance s ( E2 ) Additive standard deviation at mature age(sAm), % Diversity loss per cycle, % Rotation age, years 1 Alternative scenarios - 25 0; 100 Time before establishment of the selection test (TBEFORE), years Recombination cost (CRECOMB ), $ Cost per genotype (Cg), $ Cost per plant (Cp), $ Budget per year and parent (the constraint) Group Merit Gain per year (GMG/Y) 88 0; 38; 94 10 5; 20 0.5 0.25;1; 5 60 10; 20; 120 1 (phenotype) 3; 5 (phenotype) 5 (clone; 3; 7 (clone; phenotype/clone) phenotype/clone) 17 (progeny; 5; 7 (progeny; phenotype/progeny) phenotype/progeny) 30 0.1 (clone), 1; 5 (clone), 1 (progeny) 0.1; 5 (progeny) 1 0.5; 3 10 5; 20; 50 To be maximized Results: two-stage 2nd best •Clone = Phenotype/Clone = no need for 2 stages. 0.30 Clone 0.25 •Phenotype/Progeny is 2nd 0.20 best = best for Pine •If Progeny initiated early, may~ Phenotype/Progeny = need for a amplification •Phenotype/Progeny is shown with a restriction for Phenotype selection age > 15 Pheno/Progeny 0.15 Phenotype Progeny 0.10 1 3 5 7 9 11 13 15 17 Delay before establishment of selection test (years) arrows show main scenario If budget is cut by half = simple Phenotype test Annual Group Merit, % Budget cuts = switching to Phenotype tests in Pine 0.3 Clone Pheno/Progeny 0.2 Phenotype Progeny 0.1 0 5 10 15 20 Budget per year and parent (%) Budget cuts for Pheno/Progeny Genetic gain, % Budget = resources reallocated on cheaper Phenotype test 5 32 Stage 2 Progeny 4 17 3 5(44) Stage 1 5(72) Phenotype 2 Budget=10 Budget=5 Testing time 10 (stage 1) and 14 (stage 2) little affected by the budget Why Pheno/Progeny was so good? • It generated extra gain by taking advantage of the time before the candidates reach their sexual maturity • This was more beneficial than single-stage Progeny test at a very early age • Question for the next study: is there any feasible case where Progeny can be better? Progeny test with and without phenotypic pre-selection • Is there any realistic situation where Progeny testing is superior over Pheno/Progeny (reasonable interactions and scenarios) • What and how flat is the optimum age of pre-selection for Pheno/Progeny? (when do we will need flowers?) Phenotype test Pre-selection age? Progeny test Time and cost components CPer CYCLE = Crecomb + n (CG + m CP), Tcycle = Trecomb + TMATING + TLAG + Tprogtest TMATING age of sufficient flowering capacity to initiate progeny test (for 2-stage strategy it corresponds to the age of phenotypic pre-selection TLAG is crossing lag for progeny test (polycross, seed maturation, seedling production) Parameters study 3 Main scenario values Alternative scenario values* Interactive scenario values Additive variance (sA2 ) 1 - - Dominance variance, % of the additive variance (sD2) 25 0; 100 - Narrow-sense heritability (h2) (obtained by changing sE2) 0.1 0.01; 0.5 0.01 Additive standard deviation at mature age % 10 - - Diversity loss per cycle, % 0.5 - - L (2001) L(1980); G(2000) L(1980) 3 to 25 by 1 - - Crossing lag for progeny test (crossing; seed maturation, seedling production),years 3 5; 8 - Rotation age (RA), years 50 20; 30; 80 80 Recombination cost (CRECOMB), $ 30 0; 100 - Cost per genotype (Cg), $ 1 0.1; 10 - Cost per plant (Cp), $ 1 0.1; 2 - Budget per year and parent, $ (the constraint) 10 5; 20 - Parameters J-M genetic correlation function Age of mating for progeny test (age of sufficient flowering capacity for progeny testing), years Annual progress in Group Merit (GM/Y) 1 To be maximized J-M correlation functions • •Gwaze et al. (2000)= genetic correlations from 19 trials with 190 fams of P taeda western USA. •Lambeth (1980)= phenotypic fam mean corrs from many trials of 3 temperate conifers J-M genetic correlation coefficient •Lambeth (2001) Main = genetic corrs in 4 series (15 trials) P taeda (296 fams) 1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 Lambeth (1980) Lambeth & Dill (2001) Gwaze et al. (2000) 0.0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Ratio selection/rotation age (Q) • 2 stage strategy was better under most reasonable values •No marked loss would occur if mating is postponed to age 15 Annual Group Merit (%) Results: 2 stage is better Main scenario 0.6 Pheno/Progeny 0.3 Progeny 0.0 0 5 10 15 20 25 Age of mating for progeny test (years) J-M correlation affects pre-selection age •The gain generating efficiency mainly depends on slope of J-M correlation function. • 1.0 J-M genetic correlation coefficient •Optimum selection age depends on efficiency of Phenotype to generate enough gain to motivate prolongation of testing for an unit of time. 0.9 0.8 10 0.7 0.6 0.5 0.4 0.3 0.2 0.1 7 Gain would increase faster if switching to 12 progeny test Gain increases fast by time Lambeth (1980) Lambeth & Dill (2001) Gwaze et al. (2000) 0.0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Ratio selection/rotation age (Q) Do we have J-M estimates for spruce and pine? When the loss from optimum is important? Annual Group Merit (%) When early testing is advantageous Rotation age = 20 0.6 2 0.8 h = 0.5 Plant cost= 0.1 0.6 Pheno/Progeny 0.6 0.4 0.3 0.3 0.0 0.0 Progeny 0.2 0.0 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 Age of mating for progeny test (years) h2 is high but then Phenotype alone is better Rotation is short Plants are cheap Annual Group Merit (%) Better crossings are motivated Crossing lag= 5 0.5 0.4 0.4 Pheno/Progeny 10; 0.26 0.3 0.2 0.23 Progeny 0.3 0.1 0.0 0.0 5 10 15 20 25 10; 0.25 0.22 0.2 0.1 0 Crossing lag= 8 0.5 0 5 10 15 20 25 Age of mating for progeny test (years) Crossing lag and genotype costs had no marked effect = the crosses can be made over a longer time to simultaneously test all pre-selected individuals and their flowering may be induced at a higher cost. These are as for our interactive scenario: •low heritability (0,01), •long rotation (80 y)= less J-M at pre-selection, •weak J-M correlation (L1980) Annual Group Merit (%) Progeny is motivated when conditions disfavour Phenotype Interactive scenario 0.06 Pheno/Progeny Progeny 0.03 0.00 0 5 10 15 20 25 Age of mating for progeny test (years) But the optima flat and scenario unrealistic Optimum test time and size for pine (for one of the 50 full sib fams) Cycle time~ 27 Gain=8 % GM/Y= 0,27% Select back the best of 5 when progeny- test age is 10 Stage 2. Progenytest each of those 5 with 30 offspring 2-4 years, at a high cost if feasible Mating Long-term breeding Lag- 3-4 years Stage 1: Test 70 full-sibs Select 5 at age 10 What if no pine flowers until age 25? •Progeny is the last •Budget cuts, high h2 will favour Phenotype 0.15 0.179 0.135 0.140 Phenotype •Phenotype with selection age of 25 is better 0.20 Progeny •Pheno/Progeny is still leading Annual Group Merit, % This means, singe stage Phenotype cycle time > 25 years and For the two-stage, pre-selection not at its Main (h=0.1, budget=10), Flowers at age 25 optimum age (10 years) 0.10 0.05 0.00 Pheno/ Progeny May be 2 cycles of Phenotype instead of Pheno/Progeny? Phenotype Cycle, GM/year, GM/cycle 2 cycle s years % of Pheno 20 0,152 3,04 6,08 Pheno/Prog 40 0,181 Answer is No: 7,26 is > 6,08 7,26 Conclusions •Under all realistic values, Pheno/Progeny better than Progeny •Sufficient flowering of pine at age 10 is desirable, but the disadvantage to wait until the age of 15 years was minor, •If rotation short, h2 high, testing cheap, delays from optimum age could be important Main findings: cloning is the best strategy Our main findings Main findings- spruce Clonal test by far the best If higher h2 more clones less ramets Present plans: size 40/15, selection age: 10 years (18) (18) Select at age 15 (20) depending on J-M correlation (15) (15) (15) (15) (15) (15) With L(2001), Cycle time~ 21 Gain=8.2 % GM/Y= 0,34% Main findings- Pine Use 2 stage Pheno/Progeny strategy (70) (70) (30) (30)(30)(30)(30) (30) (30)(30)(30)(30) Stage 1 Phenotype select at age 10 (15 only 3% GM lost) Stage 2 Progeny test select at ca 10 With L(2001), Cycle time~ 27 Gain=8 % GM/Y= 0,27% Research needs- Faster cloning Research needs (a PhD thesis) •Faster, better cloning: embryogenesis, rooting, C-effects (especially for pine) •Sufficient flowering at age 10 (15) for pine •Documentation of flowering in breeding stock •How sexual maturation, flowering abundance are related to breeding value? Optimizing the Balance: restrict grandparental but relax parental contributions Balanced long-term breeding Some unbalance has advantages in long term breeding The inoptimality loss seem to be small; it is tricky to utilize inbalance, and the balance is unlikely to affect most of the recommendations much. Unbalance at initiation of breeding At initiation of breeding there is no “balance”. Truncating tested plus trees to long term breeding has sometimes been done with inoptimal unbalance in the Swedish breeding program. I believe it is more optimal to sacrify the gene diversity in the initial selection a bit slower. This has been discussed i förädlingsrådet 1999, and one argument is in Routsalainen’s thesis (2002), so I will not discuss this more here. SPM parental balance (almost current Swedish pine program) Founder selection Mating of founders Select and mate 2 best sibs to create 2 families Cycle 1 (…) (…) Select and mate 2 best sibs to create 2 families Cycle 2 (…) (…) Select and mate 2 best sibs to create 2 families Cycle 3 (…) (…) Green trees show pedigree Multiple SPMs Founders (…) Cross e.g. 4 best sibs in the 2 best families (…) 1st rank family (…) 1st rank family (…) (…) nth rank family 3rd rank family (…) 2nd rank family (…) (…) 3rd rank family (…) nth rank family (…) 2nd rank family Multiple SPMs Pedigrees BP third generation Founders (…) (…) (…) Pedigree to later breeding population Trees selected for crossing in the 3rd generation 1st rank family (…) 2nd rank family Note that retrospectively SPM and multiple SPM give identical pedigrees, thus identical increase of coancestry. . Families & parents cost nothing 0.6 14 Annual progress (%) 0.5 10 High budget 0.4 5 0.3 0.2 Medium budget Low budget 0.1 0.0 0 2 2=phenotypic 5 10 15 20 Number of parents per selected family 25 Families & parents are expensive Annual progress (%) 0.6 0.5 High budget 7 0.4 4 0.3 Medium budget 0.2 Low budget (impossible) 0.1 0.0 0 2 5 10 15 20 Number of parents per selected family Conclusions • Multiple SPM strategy is VERY promising and can beat conventional single SPM strategy with 20-70 % gain. Variants of strategy 5 which are still more efficient can be constructed. The end