* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Technicolor (physics) wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Elementary particle wikipedia , lookup
Light-front quantization applications wikipedia , lookup
ATLAS experiment wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Large Hadron Collider wikipedia , lookup
Electron scattering wikipedia , lookup
Future Circular Collider wikipedia , lookup
Quantum chromodynamics wikipedia , lookup
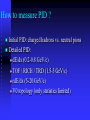
pQCD A.) pQCD components in elementary collisions B.) modification in AA collisions High pT Particle Production (the factorization theorem) Jet: A localized collection of hadrons which come from a fragmenting parton hadrons c a Parton Distribution Functions Hard-scattering cross-section b d hadrons Fragmentation Function leading particle High pT (> ~ 2.0 GeV/c) hadron production in pp collisions for √s > 60 Gev: h d pp 0 D d 2 2 h/c K dx dx f ( x , Q ) f ( x , Q ) ( ab cd ) a b a a b b 2 dyd pT dtˆ z c abcd “Collinear factorization” Hard scattering longitudinal plane Hard scattering in transverse plane Generally, partons momentum fraction x1x2. Point-like elastic scattering Partons have intrinsic transverse momentum kT (Not pT , jetin1 PHENIX pT , jet –0.35<<0.35) 2 0 pT , jet1 pT , jet 2 kT ,1 kT ,2 Jet Fragmentation (width of the jet cone) Partons have to materialize (fragment) in colorless world jT jet fragmentation transverse momentum jet jT and kT are 2D vectors. We measure the mean value of its projection into the transverse plane |jTy| and |kTy| . | k Ty | 2 |jTy| is an important jet parameter. It’s constant value independent on fragment’s pT is characteristic of jet fragmentation (jT-scaling). |kTy| (intrinsic + NLO radiative corrections) carries the information on the parton interaction with QCD medium. k AA k vac k IS nucl k FS nucl 2 2 p+p 2 p+A 2 A+A k 2T Fragmentation Function (distribution of parton momentum among fragments) pi In Principle p parton pi i | pi | cos(i ) zi | p parton | In Practice xE xE ztrigg i jet | p parton | | pi | cos(i ) i zi 1 Fragmentation function D( z ) e z / z i parton momenta are not known pT pTtrigg | pTtrigg |2 pT cos( ) =z p parton Simple relation z xE ztrigg 0 in pp: well described by NLO p+p->0 + X Thermallyshaped Soft Production “Well Calibrated” Hard Scattering Ingredients (via KKP or Kretzer) pQCD Parton distribution functions Fragmentation functions hep-ex/0305013 S.S. Adler et al. Fate of jets in heavy ion collisions? idea: p+p collisions @ same sNN = 200 GeV as reference p p ?: what happens in Au+Au to jets which pass through medium? Prediction: scattered quarks radiate energy (~ GeV/fm) in the colored medium: decreases their momentum (fewer high pT particles) “kills” jet partner on other side ? Au+Au High pT Particle Production in A+A h dN AB 2 2 ABK dx dx d k d kb a b a 2 dyd pT abcd f a / A ( xa , Q 2 ) f b / B ( xb , Q 2 ) g (k a ) g (k b ) 0 h/c * c 2 c Parton Distribution Functions Intrinsic kT , Cronin Effect S A ( xa , Qa2 ) S B ( xb , Qb2 ) d ( ab cd ) dtˆ 1 zc* dP( ) 0 zc (pQCD context…) Shadowing, EMC Effect Hard-scattering cross-section c Partonic Energy Loss D (z ,Q ) Fragmentation Function z c a b d hadrons leading particle suppressed Jet fragment shape parameters jT, kT rton distribution functions (hep-ex/0305109) RHIC o we understand hadron production elementary collisions ? (Ingredient I: PDF) RHIC Ingredient II: Fragmentation functions KKP (universality), Bourrely & Soffer (hep-ph/0305070) Non-valence quark contribution to parton fragmentation into octet baryons at low fractional momentum in pp !! Quark separation in fragmentation models is important. FFs are not universal. z z Depend on Q, Einc, and flavor How to measure PID ? Initial PID: charged hadrons vs. neutral pions Detailed PID: dE/dx (0.2-0.8 GeV/c) TOF / RICH / TRD (1.5-5 GeV/c) rdE/dx (5-20 GeV/c) V0 topology (only statistics limited) 0 in pp: well described by NLO (& LO) p+p->0 + X Thermallyshaped Soft Production “Well Calibrated” Hard Scattering Ingredients (via KKP or Kretzer) pQCD Parton distribution functions Fragmentation functions ..or simply PYTHIA… hep-ex/0305013 S.S. Adler et al. pp at RHIC: Strangeness formation in QCD nucl-ex/0607033 Strangeness production not described by leading order calculation (contrary to pion production). It needs multiple parton scattering (e.g. EPOS) or NLO corrections to describe strangeness production. Part of it is a mass effect (plus a baryon-meson effect) but in addition there is a strangeness ‘penalty’ factor (e.g. the proton fragmentation function does not describe L production). s is not just another light quark How strong are the NLO corrections in LO calculations (PYTHIA) ? K.Eskola et al. (NPA 713 (2003)): Large NLO corrections not unreasonable at RHIC energies. Should be negligible at LHC (5.5 or 14 TeV). STAR LHC New NLO calculation based on STAR data (AKK, hep-ph/0502188, Nucl.Phys.B734 (2006)) K0s apparent Einc dependence of separated quark contributions. Non-strange baryon spectra in p+p Pions agree with LO (PYTHIA) Protons require NLO with AKK-FF parametrization (quark separated FF contributions) PLB 637 (2006) 161 mt scaling in pp Breakdown of mT scaling in pp ? mT slopes from PYTHIA 6.3 Gluon dominance at RHIC PYTHIA: Di-quark structures in baryon production cause mt-shift Recombination: 2 vs 3 quark structure causes mt shift Baryon/meson ratios – p+p collisions PLB 637 (2006) 161 Bell shape from fragmentation is visible Collision Energy dependence of baryon/meson ratio Ratio vs pT seems very energy dependent (RHIC < < SPS or FNAL), LHC ? Not described by fragmentation ! (PYTHIA ratios at RHIC and FNAL are equal) Additional increase with system size in AA Both effects (energy and system size dependence) well described by recombination Recombination vs. Fragmentation (a different hadronization mechanism in medium than in vacuum ?) Recombination at moderate PT Parton pt shifts to higher hadron pt. Recomb. Fragmentation at high PT: Parton pt shifts to lower hadron pT fragmenting parton: ph = z p, z<1 recombining partons: p1+p2=ph Frag. Baryon production mechanism through strange particle correlations … 0 e e Z qq jets Test phenomenological fragmentation models OPAL ALEPH and DELPHI measurements: Yields and cosQ distribution between correlated pairs distinguishes between isotropic cluster (HERWIG) and non-isotropic string decay (JETSET) for production mechanism. Clustering favors baryon production JETSET is clearly favored by the data. Correlated LLbar pairs are produced predominantly in the same jet, i.e. short range compensation of quantum numbers. Flavor dependence of yield scaling up, down strange charm PHENIX D-mesons • participant scaling for light quark hadrons (soft production) • binary scaling for heavy flavor quark hadrons (hard production) • strangeness is not well understood (canonical suppression in pp) Charm cross-section measurements in pp collisions in STAR Charm quarks are believed to be produced at early stage by initial gluon fusions Charm cross-section should follow number of binary collisions (Nbin) scaling Measurements direct D0 (event mixing) c→+X (dE/dx, ToF) c→e+X (ToF) c→e+X (EMC) pT (GeV/c) 0.13.0 0.170.25 0.94.0 1.5 constraint , d/dpT , d/dpT d/dpT LO / NLO / FONLL? A LO calculation gives you a rough estimate of the cross section A NLO calculation gives you a better estimate of the cross section and a rough estimate of the uncertainty Fixed-Order plus Next-to-Leading-Log (FONLL) LO: Designed to cure large logs in NLO for pT >> mc where mass is not relevant Calculations depend on quark mass mc, factorization scale F (typically F = mc or 2 mc), renormalization scale R (typically R = F), parton density functions (PDF) Hard to obtain large with R = F (which is used in PDF fits) FONLL RHIC (from hep-ph/0502203 ): 400 NLO 381 cFONLL 256 b ; 244 c 146 cc 134 b 99 bbFONLL 1.8700..67 b NLO: CDF Run II c to D data (PRL 91,241804 (2003): The non-perturbative charm fragmentation needed to be tweaked in FONLL to describe charm. FFFONLL is much harder than used before in ‘plain’ NLO FFFONLL ≠ FFNLO RHIC: FONLL versus Data cc (STAR from D 0 eTOF ) cc ( FONLL) Matteo Cacciari (FONLL): factor 2 is not a problem hep-ex/0609010 factor 5 is !!! nucl-ex/0607012 Spectra in pp seem to require a bottom contribution High precision heavy quark measurements are tough at RHIC energies. Need direct reconstruction instead of semi-leptonic decays. Easy at LHC. Conclusions for RHIC pp data We are mapping out fragmentation and hadronization in vacuum as a function of flavor. What we have learned: Strong NLO contribution to fragmentation even for light quarks at RHIC energies Quark separation in fragmentation function very important. Significant nonvalence quarks contribution in particular to baryon production. Gluon dominance at RHIC energies measured through breakdown of mt-scaling and baryon/meson ratio. Unexpected small effect on baryon/antibaryon ratio Is there a way to distinguish between fragmentation and recombination ? Does it matter ? What will happen at the LHC ? What has happened in AA collisions (hadronization in matter) ? 0 in pp: well described by NLO p+p->0 + X Thermallyshaped Soft Production “Well Calibrated” Hard Scattering Ingredients (via KKP or Kretzer) pQCD Parton distribution functions Fragmentation functions hep-ex/0305013 S.S. Adler et al. Hadronization in QCD (the factorization theorem) Jet: A localized collection of hadrons which come from a fragmenting parton hadrons c a Parton Distribution Functions Hard-scattering cross-section b d hadrons Fragmentation Function leading particle High pT (>~ 2.0 GeV/c) hadron production in pp collisions: h d pp 0 D d 2 2 h/c K dx dx f ( x , Q ) f ( x , Q ) ( ab cd ) a b a a b b 2 dyd pT dtˆ zc abcd “Collinear factorization” Modification of fragmentation functions (hep-ph/0005044) RAA and high-pT suppression STAR, nucl-ex/0305015 pQCD + Shadowing + Cronin energy loss pQCD + Shadowing + Cronin + Energy Loss Deduced initial gluon density at t0 = 0.2 fm/c dNglue/dy ≈ 800-1200 ≈ 15 GeV/fm3, eloss = 15*cold nuclear matter (compared to HERMES eA) (e.g. X.N. Wang nucl-th/0307036) Is the fragmentation function modification universal ? Modification according to Gyulassy et al. (nucl-th/0302077) Octet baryon fragmentation function from statistical approach based on measured inclusive cross sections of baryons in e+e- annihilation: Induced Gluon Radiation ~collinear gluons in cone “Softened” fragmentation nchin jet : increases zin jet : decreases Quite generic (universal) but attributable to radiative rather than collisional energy loss z z Jet quenching I: hadrons are suppressed, photons are not Energy dependence of RAA 0 nucl-ex/0504001 RAA at 4 GeV: smooth evolution with √sNN Agrees with energy loss models 37 Radiative energy loss in QCD Baier, Schiff and Zakharov, AnnRevNuclPartSci 50, 37 (2000) BDMPS approximation: multiple soft collisions in a medium of static color charges Transport coefficient: qˆ medium d q q 2 Medium-induced gluon radiation spectrum: Total medium-induced energy loss: L C Emed dz d 2 d 2 2 d q dI LPM dI BetheHeitler qˆ S NC ddz lcoherent ddz dI LPM ~ S qˆC L ~ S qˆL2 ddz t formation L c E independent of parton energy (finite kinematics E~log(E)) E L2 due to interference effects (expanding medium E~L) “Jet quenching” = parton energy loss High-energy parton loses energy by rescattering in dense, hot medium. q q Described in QCD as medium effect on parton fragmentation: Medium modifies perturbative fragmentation before final hadronization in vacuo. Roughly equivalent to an effective shift in z: D p h ( z, Q ) D 2 (med) p h z ( z , Q ) D p h , Q2 1 E / E 2 Important for controlled theoretical treatment in pQCD: Medium effect on fragmentation process must be in perturbative q2 domain. Mechanisms High energy limit: energy loss by gluon radiation. Two limits: (a) Thin medium: virtuality q2 controlled by initial hard scattering (LQS, GLV) L q q g q2 (b) Thick medium: virtuality controlled by rescattering in medium (BDMPS) Trigger on leading hadron (e.g. in RAA) favors case (a). Low to medium jet energies: Collisional energy loss is competitive! Especially when the parent parton is a heavy quark (c or b). L q q Extracting qhat from hadron suppression data RAA: qhat~5-15 GeV2/fm What does qhat q̂measure? 4 2 S N C qˆ mediumxGx, qˆL 2 NC 1 ~RHIC data QGP Equilibrated gluon gas: number density ~T3 energy density ~T4 qˆ c Hadronic matter 3 4 R. Baier, Nucl Phys A715, 209c qhat+modelling energy density • pQCD result: c~2 (S? quark dof? …) • sQGP (multiplicities+hydro): c~10 Model uncertainties q-hat at RHIC RHIC data ? sQGP? QGP Pion gas Cold nuclear matter BDMPS(ASW) vs. GLV Baier, Dokshitzer, Mueller, Peigne, Schiff, Armesto, Salgado, Wiedemann, Gyulassy, Levai, Vitev Salgado and Wiedemann PRD68 (2003) 014008 E ASWBDMPS Medium-induced radiation spectrum C qˆL2 2 qˆ 2 L GLV 9 s3CR 4 Rough correspondence: (Wiedemann, HP2006) 2qˆ 0 0 d qˆ( ) L 0 L EGLV BDMPS 2 GeV fm GeV 2 qˆ 5 fm qˆ 10 sCR 2 qˆ L 4 30-50 x cold matter density 1 dN g 2 Llog E / R dy dN g 1800 dy dN g 900 dy What do we learn from RAA? GLV formalism BDMPS formalism ~15 GeV Wicks et al, nucl-th/0512076v2 Renk, Eskola, hep-ph/0610059 E=15 GeV Energy loss distributions very different for BDMPS and GLV formalisms But RAA similar! Need more differential probes RAA for 0: medium density I I. Vitev C. Loizides hep-ph/0608133v2 Use RAA to extract medium density: W. Horowitz I. Vitev: 1000 < dNg/dy < 2000 W. Horowitz: 600 < dNg/dy < 1600 C. Loizides: 6 < q̂ < 24 GeV2/fm Statistical analysis to make optimal use of data Caveat: RAA folds geometry, energy loss and fragmentation Different partons lose different amounts of energy 1.) heavy quark dead cone effect : 2.) gluon vs. quark energy loss: Heavy quarks in the vacuum and in Gluons should lose more energy the medium (Dokshitzer and and have higher particle Kharzeev (PLB 519 (2001) 199)) the multiplicities due to the color factor radiation at small angles is effect. suppressed Yu.Dokshitzer …but everything looks the same at high pt…. up,down strange charm ? Particle dependencies: RAA of strangeness A remarkable difference between RAA and RCP that seems unique to strange baryons. Ordering with strangeness content. ‘Canonical suppression’ is unique to strange hadrons This effect must occur ‘between’ pp and peripheral AA collisions Strange enhancement vs. charm suppression ? Do strange particles hadronize different than charm particles ? But is it a flavor effect ? Kaon behaves like D-meson, we need to measure Lc An important detail: the medium is not totally opaque There are specific differences to the flavor of the probe plus: heavy quarks also show effects of collisional e-loss Experiment: there are baryon/meson differences Theory: there are two types of e-loss: radiative and collisional, plus dead-cone effect for heavy quarks Flavor dependencies map out the process of in-medium modification BUT: heavy quarks show same e-loss than light quarks RAA of electrons from heavy flavor decay Describing the suppression is difficult for models radiative energy loss with typical gluon densities is not enough (Djordjevic et al., PLB 632(2006)81) models involving a very opaque medium agree better (qhat very high !!) (Armesto et al., PLB 637(2006)362) collisional energy loss / resonant elastic scattering (Wicks et al., nucl-th/0512076, van Hees & Rapp, PRC 73(2006)034913) heavy quark fragmentation and dissociation in the medium → strong suppression for charm and bottom (Adil & Vitev, hep-ph/0611109) Constraining medium viscosity /s Simultaneous description of STAR R(AA) and PHENIX v2 for charm. (Rapp & Van Hees, PRC 71, 2005) Ads/CFT == /s ~ 1/4 ~ 0.08 Perturbative calculation of D (2t) ~6 (Teaney & Moore, PRC 71, 2005) == /s~1 transport models require small heavy quark relaxation time small diffusion coefficient DHQ x (2T) ~ 4-6 this value constrains the ratio viscosity/entropy /s ~ (1.3 – 2) / 4 within a factor 2 of conjectured lower quantum bound consistent with light hadron v2 analysis electron RAA ~ 0 RAA at high pT - is bottom suppressed as well? Energy density of matter high energy density: > 1011 J/m3 P > 1 Mbar I > 3 X 1015W/cm2 Fields > 500 Tesla QGP energy density > 1 GeV/fm3 i.e. > 1030 J/cm3