* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint Slides
Futures contract wikipedia , lookup
Futures exchange wikipedia , lookup
Local authorities swaps litigation wikipedia , lookup
Collateralized mortgage obligation wikipedia , lookup
Black–Scholes model wikipedia , lookup
Employee stock option wikipedia , lookup
Option (finance) wikipedia , lookup
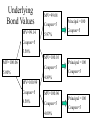
Financial Risk Management of Insurance Enterprises Valuing Interest Rate Options and Swaps Interest Rate Options • We will take a more detailed look at interest rate options • What is fraternity row? – Delta, gamma, theta, kappa, vega, rho • What is the Black-Scholes formula? – What are its limitations for interest rate options? • How do we value interest rate options using the binomial tree method? • What is an implied volatility? Price Sensitivity of Options • Before moving to options on bonds, let’s digress to the “simpler” case of options on stock • Define delta (∆) as the change in the option price for a change in the underlying stock • Recall that at maturity c=max(0,ST-X) and p=max(0,X-ST) – This should help make the sign of the derivatives obvious Definition of Delta c For calls, = 0 S p For puts, = 0 S c = call value S = stock price p = put value Predicting Changes in Option Value • We can use delta to predict the change in the option value given a change in the underlying stock • For example, if ∆= -½, what is the change in the option value if the stock price drops by $5 – First, the option must be a put since ∆<0 – We know that puts increase in value as S decreases – Change in put is (-½) x (-5) = +2.50 Similarity to Duration • Note that ∆ is similar to duration • The analog of convexity for options is called gamma (γ) – This measures the curvature of the price curve as a function of the stock price Call value Call price – It predicts the change in value based on a linear relationship Intrinsic value X Stock price Delta Other Greeks • Recall that the value of an option depends on: – – – – – Underlying stock price (S) Exercise price (X) Time to maturity (T) Volatility of stock price (σ) Risk free rate (rf) • The only thing that is not changing is the exercise price • Define “the greeks” by the partial derivatives of the option’s value with respect to each independent variable Other Greeks (p.2) • We’ve already seen the first and second derivative with respect to S (∆ and γ) c Theta = T c Kappa = ; Also known as " vega" c Rho = rf Black-Scholes • Black and Scholes have developed an arbitrage argument for pricing calls and puts • The general argument: – Form a hedge portfolio with 1 option and ∆ shares of the underlying stock – Any instantaneous movement of the stock price is exactly offset by the change in the option – Resulting portfolio is riskless and must earn risk-free rate The Black-Scholes Formula • After working through the argument, the result is a partial differential equation which has the following solution C S N ( d1 ) X e rf t N (d 2 ) 2 ) ( rf )t X 2 d1 t d 2 d1 t ln( S N () cumulative distribution function of a standard normal random variable Some Comments about BlackScholes • Formula is for a European call on a nondividend paying stock • Based on continuous hedging argument • To value put options, use put-call parity relationship • It can be shown that ∆ for a call is N(d1) – This is not as easy as it may look because S shows up in d1 and d2 Problems in Applying BlackScholes to Bonds • There are three issues in applying Black-Scholes to bonds • First, the assumption of a constant risk-free rate is harmless for stock options – For bonds, the movement of interest rates is why the option “exists” • Second, constant volatility of stocks is a reasonable assumption – But, as bonds approach maturity, volatility decreases since at bond maturity, it can only take on one value Problems in Applying BlackScholes to Bonds (p.2) • Third, assuming that interest rates cannot be negative, there is an upper limit on bond prices that does not exist for stocks – Max price is the undiscounted value of all cash flows • Another potential problem is that most bonds pay coupons – Although, there are formulae which compute the option values of dividend-paying stocks Binomial Method • Instead of using Black-Scholes, we can use the binomial method • Based on the binomial tree, we can value interest rate options in a straightforward manner • What types of options can we value? – Calls and puts on bonds – Caps and floors Example of Binomial Method • What is the value of a 2 year call option if the underlying bond is a 3 year, 5% annual coupon bond – The strike price is equal to the face value of $100 • Assume we have already calibrated the binomial tree so that we can price the bond at each node – Make sure our binomial model is “arbitrage free” by replicating market values of bonds Underlying Bond Values MV=99.14 MV=99.08 Coupon=5 5.97% Principal =100 Coupon=5 Coupon=5 5.50% MV=100.10 MV=100.06 Coupon=5 5.00% Principal =100 Coupon=5 4.89% MV=100.99 Coupon=5 4.50% MV=100.96 Coupon=5 4.00% Principal =100 Coupon=5 Option Values • Start at expiration of option and work backwards – Option value at expiration is max(0,ST-X) • Discount payoff to beginning of tree MV=0.05 MV=0.27 5.00% Option Value = 0 5.50% Option Value = 0.10 MV=0.51 4.50% Option Value = 0.96 Calculations Final Payoffs max( 0, BT 100) BT is Bond value at option expiration 0 0.10 0.05 = 2 1.055 0.10 0.96 0.51 2 1.045 0.05 0.51 0.27 2 1.05 A Note About Options on Bonds • A call option on a bond is similar to a floor – As interest rates decline, the underlying bond price increases and the call value increases in value – A floor also pays off when interest rates decline • Main difference lies in payoff function – For floors, the payoff is linear in the interest rate – For call options, the payoff has curvature because the bond price curve is convex Implied Volatility • Using the Black-Scholes equation or a binomial tree is useful if volatility is known – Historical volatility is frequently used • Using the market prices of options, we can “back into” an implied market volatility – Use solver tool in spreadsheet programs or just use trial-and-error Use of Implied Volatility • When creating a binomial model or similar type of tool, we should make sure that the implied market volatility is consistent with our model • If our model has assumed a low volatility relative to the market, we are underpricing options • This is an additional “constraint” along with arbitrage-free considerations Interest Rate Swaps • Swaps are used frequently by insurers • Importance of swaps requires us to look more deeply into their pricing • What are some market conventions? • How to we value swaps? – How do we value the floating side? – How do we determine the fixed rate? Review • Recall that in an interest rate swap, two parties exchange periodic interest payments on a notional principal amount • Typically, one interest rate is a floating rate and the other is the fixed rate • Markets refer to swap positions based on fixed vs. floating position – Purchasing a swap or being long a swap refers to paying the fixed rate (receiving floating) The Most Common Contract • We look at the most common contract because it has quotes which are readily available – Quarterly settlement (four payments per year) – Floating rate is 90-day (3-month) LIBOR “flat” • Other swap contracts may be less liquid and have a higher spread – May require a moderate amount of calculations • We will price swaps assuming this common contract Conventions in Fabozzi vs. Our Convention • The book uses the following conventions – A 360-day year is assumed – Payments are based on the interest rate prorated by the actual number of days in the quarter (called “actual/360 basis”) • Others use actual/365 for the fixed side • NOTE: FOR SIMPLICITY, WE WILL USE COMMON SENSE AND NOT MARKET CONVENTIONS – One-quarter year is ¼, not “actual/360” Pricing Swaps - Overview • Recall that Eurodollar CD futures are based on the 3-month LIBOR contract – Underlying is the 3-month, future LIBOR • See WSJ for Eurodollar futures prices – Recall from Chapter 10, the future LIBOR is 100 minus the index price • Hedging arguments require liquidity – Eurodollar futures are the most heavily traded futures contracts in the world – Liquidity is excellent for 5-7 years Pricing Swaps - Overview (p.2) • By establishing a hedging argument, we can “replicate” the swap with Eurodollar futures • A swap can be decomposed into two pieces: a position in a floating rate bond and the opposite position in a fixed rate bond – If long a swap, you are long the fixed bond and short the floating bond Valuing the Floating Side • Essentially, we are pricing a floating rate bond – Cash flow depends on what the coupon is based on (e.g. LIBOR, Treasuries) • If the floating payments are based on LIBOR, as in the swap case: – We can use Eurodollar CD futures to determine an implied future floating rate – This gives us the “unknown” future floating payment on the swap Determining the Fixed Rate • As in the simple two period case, we want swap NPV=0 • Use trial-and-error (or some solver) to determine the fixed rate which will have the same present value as the floating side • Pricing an interest rate swap becomes a question of finding the fixed rate An Example • What is the fixed rate for a 2-year swap given the following Eurodollar future prices? • Assume it is December 2005, the current 3month LIBOR is 4.50%, and the notional amount is $1 million Example - Eurodollar Futures Prices Maturity Index Price March 06 95.00 June 06 94.50 Sep 06 94.00 Dec 06 93.75 March 07 93.50 June07 93.25 Sep 07 93.00 Dec 07 92.75 Example - Floating Rate Value Payment Dec-05 Mar-06 Jun-06 Sep-06 Dec-06 Mar-07 Jun-07 Sep-07 Dec-07 Futures Forward Discount Price Rate Factor Float CF PV Float 4.50% 1.00000 95.00 5.00% 0.98888 11,250 11,125 94.50 5.50% 0.97667 12,500 12,208 94.00 6.00% 0.96342 13,750 13,247 93.75 6.25% 0.94918 15,000 14,238 93.50 6.50% 0.93458 15,625 14,603 93.25 6.75% 0.91964 16,250 14,944 93.00 7.00% 0.90437 16,875 15,261 92.75 7.25% 0.88882 17,500 15,554 Total 111,180 Example - Sample Calculations 1 Discount1 0.98888 1 0.25 0.045 1 Discount2 0.98888 0.97667 1 0.25 0.05 Payment1 1,000,000 0.25 0.045 11,250 Payment2 1,000,000 0.25 0.05 12,500 Note About Discount Factors • This approach gives us another source of interest rate information – We use the Eurodollar Futures contracts – Previously, we used the Treasury curve • There will be a difference in the interest rates represented by LIBOR vs. Treasuries due to credit risk – LIBOR has credit risk Determine the Fixed Rate • Use the discount rates to “guess” a fixed rate of the swap • Equate the fixed side value of the swap to the floating side value Example - Finding the Fixed Rate Payment Dec-05 Mar-06 Jun-06 Sep-06 Dec-06 Mar-07 Jun-07 Sep-07 Dec-07 Target Forward Discount Rate Factor 4.50% 1.00000 5.00% 0.98888 5.50% 0.97667 6.00% 0.96342 6.25% 0.94918 6.50% 0.93458 6.75% 0.91964 7.00% 0.90437 7.25% 0.88882 111,180 Fixed at 5% 12,500 12,500 12,500 12,500 12,500 12,500 12,500 12,500 PV of 5% 12,361 12,208 12,043 11,865 11,682 11,495 11,305 11,110 94,069 Fixed at 7% 17,500 17,500 17,500 17,500 17,500 17,500 17,500 17,500 PV of 7% 17,305 17,092 16,860 16,611 16,355 16,094 15,827 15,554 131,697 Using Goal Seek in Excel, Fixed Rate of Swap is 5.91% Valuing an Off-Market Swap • Off-market means that the fixed rate is not the rate in a new swap – Therefore, NPV is not necessarily 0 • Value the floating payments using Eurodollar futures as before • Value the fixed side using the discount rates for the floating side • Difference of floating side and fixed side is the value of the swap Next Lecture • Dynamic Financial Analysis • Review for the Second Exam