Download PowerPoint Slides

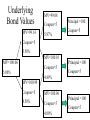
Financial Risk Management of
Insurance Enterprises
Valuing Interest Rate Options and
Swaps
Interest Rate Options
• We will take a more detailed look at interest
rate options
• What is fraternity row?
– Delta, gamma, theta, kappa, vega, rho
• What is the Black-Scholes formula?
– What are its limitations for interest rate options?
• How do we value interest rate options using
the binomial tree method?
• What is an implied volatility?
Price Sensitivity of Options
• Before moving to options on bonds, let’s
digress to the “simpler” case of options on
stock
• Define delta (∆) as the change in the option
price for a change in the underlying stock
• Recall that at maturity c=max(0,ST-X) and
p=max(0,X-ST)
– This should help make the sign of the
derivatives obvious
Definition of Delta
c
For calls,  =
0
S
p
For puts,  =
0
S
c = call value
S = stock price
p = put value
Predicting Changes in Option
Value
• We can use delta to predict the change in the
option value given a change in the underlying
stock
• For example, if ∆= -½, what is the change in
the option value if the stock price drops by $5
– First, the option must be a put since ∆<0
– We know that puts increase in value as S
decreases
– Change in put is (-½) x (-5) = +2.50
Similarity to Duration
• Note that ∆ is similar to
duration
• The analog of convexity
for options is called
gamma (γ)
– This measures the
curvature of the price
curve as a function of the
stock price
Call value
Call price
– It predicts the change in
value based on a linear
relationship
Intrinsic value
X
Stock price
Delta
Other Greeks
• Recall that the value of an option depends on:
–
–
–
–
–
Underlying stock price (S)
Exercise price (X)
Time to maturity (T)
Volatility of stock price (σ)
Risk free rate (rf)
• The only thing that is not changing is the
exercise price
• Define “the greeks” by the partial derivatives of
the option’s value with respect to each
independent variable
Other Greeks (p.2)
• We’ve already seen the first and second
derivative with respect to S (∆ and γ)
c
Theta =  
T
c
Kappa =  
; Also known as " vega"

c
Rho =  
 rf
Black-Scholes
• Black and Scholes have developed an
arbitrage argument for pricing calls and puts
• The general argument:
– Form a hedge portfolio with 1 option and ∆
shares of the underlying stock
– Any instantaneous movement of the stock price
is exactly offset by the change in the option
– Resulting portfolio is riskless and must earn
risk-free rate
The Black-Scholes Formula
• After working through the argument, the
result is a partial differential equation which
has the following solution
C  S  N ( d1 )  X  e
 rf t
N (d 2 )
2

)  ( rf 
)t
X
2
d1 
 t
d 2  d1   t
ln( S
N ()  cumulative distribution function
of a standard normal random variable
Some Comments about BlackScholes
• Formula is for a European call on a nondividend paying stock
• Based on continuous hedging argument
• To value put options, use put-call parity
relationship
• It can be shown that ∆ for a call is N(d1)
– This is not as easy as it may look because S
shows up in d1 and d2
Problems in Applying BlackScholes to Bonds
• There are three issues in applying Black-Scholes
to bonds
• First, the assumption of a constant risk-free rate is
harmless for stock options
– For bonds, the movement of interest rates is why the
option “exists”
• Second, constant volatility of stocks is a
reasonable assumption
– But, as bonds approach maturity, volatility decreases
since at bond maturity, it can only take on one value
Problems in Applying BlackScholes to Bonds (p.2)
• Third, assuming that interest rates cannot be
negative, there is an upper limit on bond
prices that does not exist for stocks
– Max price is the undiscounted value of all cash
flows
• Another potential problem is that most
bonds pay coupons
– Although, there are formulae which compute
the option values of dividend-paying stocks
Binomial Method
• Instead of using Black-Scholes, we can use
the binomial method
• Based on the binomial tree, we can value
interest rate options in a straightforward
manner
• What types of options can we value?
– Calls and puts on bonds
– Caps and floors
Example of Binomial Method
• What is the value of a 2 year call option if the
underlying bond is a 3 year, 5% annual
coupon bond
– The strike price is equal to the face value of $100
• Assume we have already calibrated the
binomial tree so that we can price the bond at
each node
– Make sure our binomial model is “arbitrage free”
by replicating market values of bonds
Underlying
Bond Values
MV=99.14
MV=99.08
Coupon=5
5.97%
Principal =100
Coupon=5
Coupon=5
5.50%
MV=100.10
MV=100.06
Coupon=5
5.00%
Principal =100
Coupon=5
4.89%
MV=100.99
Coupon=5
4.50%
MV=100.96
Coupon=5
4.00%
Principal =100
Coupon=5
Option Values
• Start at expiration of option and work backwards
– Option value at expiration is max(0,ST-X)
• Discount payoff to beginning of tree
MV=0.05
MV=0.27
5.00%
Option Value = 0
5.50%
Option Value = 0.10
MV=0.51
4.50%
Option Value = 0.96
Calculations
Final Payoffs  max( 0, BT  100)
BT is Bond value at option expiration
0  0.10
0.05 =
2
1.055
0.10  0.96
0.51 
2
1.045
0.05  0.51
0.27 
2
1.05
A Note About Options on Bonds
• A call option on a bond is similar to a floor
– As interest rates decline, the underlying bond
price increases and the call value increases in
value
– A floor also pays off when interest rates decline
• Main difference lies in payoff function
– For floors, the payoff is linear in the interest rate
– For call options, the payoff has curvature because
the bond price curve is convex
Implied Volatility
• Using the Black-Scholes equation or a
binomial tree is useful if volatility is known
– Historical volatility is frequently used
• Using the market prices of options, we can
“back into” an implied market volatility
– Use solver tool in spreadsheet programs or just
use trial-and-error
Use of Implied Volatility
• When creating a binomial model or similar
type of tool, we should make sure that the
implied market volatility is consistent with
our model
• If our model has assumed a low volatility
relative to the market, we are underpricing
options
• This is an additional “constraint” along with
arbitrage-free considerations
Interest Rate Swaps
• Swaps are used frequently by insurers
• Importance of swaps requires us to look
more deeply into their pricing
• What are some market conventions?
• How to we value swaps?
– How do we value the floating side?
– How do we determine the fixed rate?
Review
• Recall that in an interest rate swap, two
parties exchange periodic interest payments
on a notional principal amount
• Typically, one interest rate is a floating rate
and the other is the fixed rate
• Markets refer to swap positions based on
fixed vs. floating position
– Purchasing a swap or being long a swap refers to
paying the fixed rate (receiving floating)
The Most Common Contract
• We look at the most common contract because
it has quotes which are readily available
– Quarterly settlement (four payments per year)
– Floating rate is 90-day (3-month) LIBOR “flat”
• Other swap contracts may be less liquid and
have a higher spread
– May require a moderate amount of calculations
• We will price swaps assuming this common
contract
Conventions in Fabozzi vs. Our
Convention
• The book uses the following conventions
– A 360-day year is assumed
– Payments are based on the interest rate prorated by
the actual number of days in the quarter (called
“actual/360 basis”)
• Others use actual/365 for the fixed side
• NOTE: FOR SIMPLICITY, WE WILL USE
COMMON SENSE AND NOT MARKET
CONVENTIONS
– One-quarter year is ¼, not “actual/360”
Pricing Swaps - Overview
• Recall that Eurodollar CD futures are based
on the 3-month LIBOR contract
– Underlying is the 3-month, future LIBOR
• See WSJ for Eurodollar futures prices
– Recall from Chapter 10, the future LIBOR is
100 minus the index price
• Hedging arguments require liquidity
– Eurodollar futures are the most heavily traded
futures contracts in the world
– Liquidity is excellent for 5-7 years
Pricing Swaps - Overview (p.2)
• By establishing a hedging argument, we can
“replicate” the swap with Eurodollar futures
• A swap can be decomposed into two pieces:
a position in a floating rate bond and the
opposite position in a fixed rate bond
– If long a swap, you are long the fixed bond and
short the floating bond
Valuing the Floating Side
• Essentially, we are pricing a floating rate
bond
– Cash flow depends on what the coupon is based
on (e.g. LIBOR, Treasuries)
• If the floating payments are based on
LIBOR, as in the swap case:
– We can use Eurodollar CD futures to determine
an implied future floating rate
– This gives us the “unknown” future floating
payment on the swap
Determining the Fixed Rate
• As in the simple two period case, we want
swap NPV=0
• Use trial-and-error (or some solver) to
determine the fixed rate which will have the
same present value as the floating side
• Pricing an interest rate swap becomes a
question of finding the fixed rate
An Example
• What is the fixed rate for a 2-year swap
given the following Eurodollar future
prices?
• Assume it is December 2005, the current 3month LIBOR is 4.50%, and the notional
amount is $1 million
Example - Eurodollar Futures
Prices
Maturity
Index Price
March 06
95.00
June 06
94.50
Sep 06
94.00
Dec 06
93.75
March 07
93.50
June07
93.25
Sep 07
93.00
Dec 07
92.75
Example - Floating Rate Value
Payment
Dec-05
Mar-06
Jun-06
Sep-06
Dec-06
Mar-07
Jun-07
Sep-07
Dec-07
Futures Forward Discount
Price
Rate
Factor Float CF PV Float
4.50% 1.00000
95.00
5.00% 0.98888
11,250
11,125
94.50
5.50% 0.97667
12,500
12,208
94.00
6.00% 0.96342
13,750
13,247
93.75
6.25% 0.94918
15,000
14,238
93.50
6.50% 0.93458
15,625
14,603
93.25
6.75% 0.91964
16,250
14,944
93.00
7.00% 0.90437
16,875
15,261
92.75
7.25% 0.88882
17,500
15,554
Total
111,180
Example - Sample Calculations
1
Discount1 
 0.98888
1  0.25  0.045
1
Discount2  0.98888
 0.97667
1  0.25  0.05
Payment1  1,000,000  0.25  0.045  11,250
Payment2  1,000,000  0.25  0.05  12,500
Note About Discount Factors
• This approach gives us another source of
interest rate information
– We use the Eurodollar Futures contracts
– Previously, we used the Treasury curve
• There will be a difference in the interest
rates represented by LIBOR vs. Treasuries
due to credit risk
– LIBOR has credit risk
Determine the Fixed Rate
• Use the discount rates to “guess” a fixed
rate of the swap
• Equate the fixed side value of the swap to
the floating side value
Example - Finding the Fixed Rate
Payment
Dec-05
Mar-06
Jun-06
Sep-06
Dec-06
Mar-07
Jun-07
Sep-07
Dec-07
Target
Forward Discount
Rate
Factor
4.50% 1.00000
5.00% 0.98888
5.50% 0.97667
6.00% 0.96342
6.25% 0.94918
6.50% 0.93458
6.75% 0.91964
7.00% 0.90437
7.25% 0.88882
111,180
Fixed
at 5%
12,500
12,500
12,500
12,500
12,500
12,500
12,500
12,500
PV
of 5%
12,361
12,208
12,043
11,865
11,682
11,495
11,305
11,110
94,069
Fixed
at 7%
17,500
17,500
17,500
17,500
17,500
17,500
17,500
17,500
PV
of 7%
17,305
17,092
16,860
16,611
16,355
16,094
15,827
15,554
131,697
Using Goal Seek in Excel, Fixed Rate of Swap is 5.91%
Valuing an Off-Market Swap
• Off-market means that the fixed rate is not
the rate in a new swap
– Therefore, NPV is not necessarily 0
• Value the floating payments using
Eurodollar futures as before
• Value the fixed side using the discount rates
for the floating side
• Difference of floating side and fixed side is
the value of the swap
Next Lectures
• Interest Rate Sensitivity
• Dynamic Financial Analysis
• Securitizing Catastrophe Risk